物理所之行学术总结 凝聚态计算方法（2）

数值化重整化群

Wilson通过有效场论的思想提出的重整化群理论可以有效的考察体系中的各种参数随着体系的能标或者尺度而变化的一个规律，当从一个高能标向一个能标低一点的理论过度时，可以将两个能标间的快场（小尺度的涨落）积掉或者说做一个平均，更结合体系在相变点的物理量有一个自相似的特点，把相变点和重整化的参数流方程的不动点（更具体来讲对于一个多变量的参数流方程，其应是一个鞍点，即其中某些参数在这个点上取极大而某些则取极小），进而我们可以利用重整化的理论来考虑体系在相变点（或量子相变点）的一些特性。

上述思想在理论解析的计算一些具体的格点模型时，当然可以把格点的模型连续化，进而使用场论的语言来进行推导和计算。

一般标准步骤就是，第一步把一个指定能标下的模型中的场，分为快场和慢场，即

\phi(x)=\int_{|k|<\Lambda}\phi_k e^{ikx} \mapsto \phi=\phi_f+\phi_s

其中快场和慢场分别的定义则是

\phi_{f} \rightarrow \int_{\Lambda/b<|k|<\Lambda},\phi_{s} \rightarrow \int_{|k|<\Lambda/b}

进而根据这个场的分割将作用量也划分为三部分

S=S_{f}[\phi_{f}]+S_{s}[\phi_{s}]+S_{c}[\phi_{f},\phi_{s}]

下面进入第二步，进行快场部分的路径积分，将高能标部分的场全部积掉，而得到一个在低能标下的有效作用量，这个有效作用量的定义即为

exp[-S_{eff}]=exp[-S_{s}[\phi_{s}]<exp[-S_{c}[\phi_{f},\phi_{s}]>_{f}

这个部分是整个理论计算的核心，大部分情况下要做一些近似，并且快场的计算贡献的会是一些圈图，而这些圈图会使计算时引入一些发散，所以在计算时也会使用例如维数正规化这样的一个技巧，来形式上避免这些发散的产生。并且在这一步中，有效作用量中会出现大量跟问题不相关的局域项，在计算过程中我们也只需要来保留跟问题相关的那几项进行计算。

当第二步完成之后，我们会发现得到了一个低能标的有效场论，并且场论模型中的参数是与之前分割快慢场时定义的b有关。我们可以认为一开始所谓的高能标的物理也是通过更高能标的物理将快场积掉而得到的，所以我们要将这个有效场论中的物理量进行k\mapsto k_{new}=bk 重新标度化，进而在形式上得到一个能标与原来相同的有效理论，参数依然跟b这样的人为引入的参数，定义参数对于lnb的求导得到的微分方程为参数流方程，这个参数流方程的不动点正是我们所关心的。引入b这样一个参数，并且依据这个参数进行重新标度，正是将考察体系尺度缩小的一个过程，相变点有一个重要的特性就是关联长度趋于无穷，而这样一个性质恰恰是在体系尺度做重新标度化下是不变的，所以把对lnb求导的不动点与相变点联系起来。

这是在理论推导时大致的一个思路，不过理论推导有一个弊端，在第二步的计算常常以一个微扰级数的形式在展开，在强关联系统里面这样的一个方法不免要失去一定的有效性，所以我们也要从格点模型出发开发出一套行之有效的数值计算手段，这就是这一节后半部分要简要介绍的数值重整化群方法（NRG）（Bulla2007The）

其大致思想可以概括为，首先对于一个模型，我们可以把它类似于动力学平均场的分割方法，分为杂质项，杂质与周围粒子的耦合项，和周围粒子项即

H=H_{imp}+H_{bath}+H_{imp-bath}

对于单杂质的周期Anderson模型上面的三项分别为

H_{imp}=\sum_{\sigma}\epsilon_{f}f_{\sigma}^{\dag}f_{\sigma}+Uf_{\uparrow}^{\dag}f_{\uparrow}f_{\downarrow}^{\dag}f_{\downarrow}H_{bath}=\sum_{k\sigma}\epsilon_{k}c_{k\sigma}^{\dag} c_{k\sigma}
H_{imp-bath}=\sum_{k\sigma}V_{k}f_{\sigma}^{\dag}c_{k\sigma}+c_{k\sigma}^{\dag} f_{\sigma}

下面可以把上面的这个格点模型利用一定的技巧转化到能量表像下

H=H_{imp}+\sum_{\sigma}\int_{-1}^{1}d\epsilon g(\epsilon)a_{\epsilon\sigma}^{\dag}a_{\epsilon\sigma}+\sum_{\sigma}\int_{-1}^{1}d\epsilon g(\epsilon)f_{\sigma}^{\dag}a_{\epsilon\sigma}+a_{\epsilon\sigma}^{\dag}f_{\sigma}

有了这个表达式，我们考虑把能量区间做一个分割，并且注意在前面重整化的理论中，我们实际是探求了原来能标除以b的以后的新能标的有效理论，但如果把这个步骤继续下去，如果我们只想探求b^{-n}以下的理论，那么我们就需要依次将[b^{-1},1]到[b^{-n},b^{-n-1}]的区间中的场依次积掉，故提示了我们在这里一个合理的分割为一个对数分割

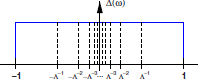
对于这样一个能量分割，我们可以定义只存在于每个相应区间中的一个组完备基即在每个区间内是一组平面波，而在区间外则为零

这样可以把在能量表象中的产生算符用着一系列基来展开

a_{\epsilon\sigma}=\sum_{np}[a_{np\sigma}\psi_{np}^{+}(\epsilon)+b_{np\sigma}\psi_{np}^{-}(\epsilon)

利用这个表达式经过一系列比较复杂的运算后，得到了一个新的hamilton量

H=H_{imp}+\sum_{n\sigma}(\xi_{n}^{+}a_{n\sigma}^{\dag}a_{n\sigma}+\xi_{n}^{-}b_{n\sigma}^{\dag}b_{n\sigma})+\frac{1}{\sqrt{\pi}}\sum_{\sigma}f_{\sigma}^{\dag}\sum_{n}(\gamma_{n}^{+}a_{n\sigma}+\gamma_{n}^{-}b_{n\sigma})+\frac{1}{\sqrt{\pi}}\sum_{\sigma}(\sum_{n}(\gamma_{n}^{+}a_{n\sigma}+\gamma_{n}^{-}b_{n\sigma}))f_{\sigma}

在计算计算之前我们可以稍微观查一下上面这个式子，如果把a(b)理解为第n个区间上的一个粒子（反粒子）的产生算符的话，那么这个hamilton量很类似于一个在一维上n+1个格点上的一个hamilton量，其中第0个格点第一个上为杂质，剩下的格点上则是存在于第n个能量区间的一个粒子（或反粒子）。正是因为如此，我们就要把上面的这个哈密顿量经过一定的处理映射为一个半无限长的链上hamilton量。

可以将a_n和b_n重新进行一定的组合构成一个c_n来化简得到的hamilton量，这个c的算符跟原来的模型中导带电子的产生湮灭算符是不一样的，不过是可以建立起一定对应关系的

c_{n\sigma}=\sum_{m=0}^{\infty}(u_{nm}a_{m\sigma}+v_{nm}b_{m\sigma})

并将c_0定义为

c_{n\sigma}=\frac{1}{\xi_{0}}\sum_{n}(\gamma_{n}^{+}a_{n\sigma}+\gamma_{n}^{-}b_{m\sigma})

最终把hamilton量化为

H=H_{imp}+\sqrt{\frac{\xi_0}{\pi}}\sum_{\sigma}(f_{\sigma}^{\dag}c_(0\sigma)+c_(0\sigma)^{\dag}(f_{\sigma})+\sum_{\sigma n=0}^{\infty}[\epsilon_n c_{n\sigma}^{\dag}c_{n\sigma}+t_{n}(c_{n\sigma}^{\dag}c_{n+1\sigma}+c_{n+1\sigma}^{\dag}c_{n\sigma})]

图像为

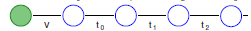
由于这个模型是由原来的单杂质anderson模型转化而来的，估这个模型中的参数都可以被原来的模型中参数来表达，具体的表达也可参考相关文献

而这个模型还是没有办法进行精确的计算，我们还是要再化简，我们求一个只有N个格点时是可以精确计算的，然后我们可以保留原来N个格点的精确结果中的本征矢，继续和第N+1个格点的状态做一个直积，便得到N+1个格点的模型的一组积，然后在这组基下对角化第N+1个hamilton量，依次类推，一直计算到N趋近于无穷时，便可以得到关于原来模型的一个数值解了。

首先定义，N加一个杂质的hamilton量为

H_N=\Gamma^(N-1)/2(H_{imp}+\sqrt{\frac{\xi_0}{\pi}}\sum_{\sigma}(f_{\sigma}^{\dag}c_(0\sigma)+c_(0\sigma)^{\dag}(f_{\sigma})+\sum_{\sigma n=0}^{N}\epsilon_n c_{n\sigma}^{\dag}c_{n\sigma}+\sum_{\sigma n=0}^{N-1}t_{n}(c_{n\sigma}^{\dag}c_{n+1\sigma}+c_{n+1\sigma}^{\dag}c_{n\sigma}))

以及N趋向无穷的一个极限

H=\lim \Gamma^{-(N-1)/2}H_{N}

额外的因子是为了讨论一些问题的方便，这里的这个因子是为了讨论体系重整化流的方便。我们可以看到第$H_N$的一个递推关系

H_{N+1}=\sqrt{\Gamma}H_N+\Gamma^{N/2}[\sum_{\sigma}\epsilon_{N+1}c_{N+1\sigma}^{\dag}c_{N+1\sigma}+\sum_{\sigma}t_{N}(c_{N\sigma}^{\dag}c_{N+1\sigma}+c_{N+1\sigma}^{\dag}c_{N\sigma})]

这很类似于我们前面在一个高能标下的作用量和一个低能标下的有效作用量通过积掉快场联系起来，并且注意到实际H_N和H_{N+1}差的信息就是是映射后模型的第N+1个格点，而这恰恰对应于位于第N个能量区间的一个快场。

接下来就是具体的计算问题了，首先我们可以把N比较小的H_N精确对角化，然后求得相应的本征值和本征矢，进而按前面的方法进行递推。但如果一开始的本征值个数为N_1后来每个新加的格点都有一个自由度是$m$，那么随着格点数的增加矩阵元素的个数是m^2的的指数量级在增加，这样加过几个格点后矩阵的精确对角化肯定是不可能完成的，由此，我们需要在每次计算时都保留一定数量的相同数量的本征值，这样在没新加进一个格点时其所要进行对角化的元素数量都是相同的，我们一般选择保留能量最低的那几个本征矢进行进一步计算。而且由于每次都是产生相同数量的本征值以及本征矢，则我们可以考察对应的能量本征值随着计算过的格点个数的一个变化规律，这与之前在重整化理论中参数随lnb的变化一样，都是重整化流如下图所示

之后我们可以根据数值重整化群所计算得到的信息，进而计算得一些物理量，从而得到关于材料的一些有效预言。

总结

以上便是所有在实习阶段了解和学习到的凝聚态理论和计算方面的一些知识，通过实习也可以发现，在课本上学到的东西是可以帮助我们理解在科研中用到一些新知识，所以要想做出出色的结果，一定是要由厚实的结果，可以触类旁通、举一反三。而且通过实现，也对数值计算这个领域有了一些全新的认识。一个好的数值计算结果，一定是取决于做的人的物理直觉和丰富经验，如果想要做出出色的数值结果也是十分不容易的。这一点在自己上手做二维ising模型的时候便深有体会。最后感谢杨义峰研究员，老徐以及各位博士师兄的引导和建议，还有与我一同在重费米子组实习的小伙伴们，和你们的讨论让我收获颇丰。