【最优化】无约束优化方法-牛顿法

一、前言

在最速梯度下降法中：

可以知道迭代点的更新为：

x^{k+1}=x^{k}+t_{k}df(x^{k}) ,可以看到只用到了目标函数的一阶导数信息（迭代方向），而牛顿法则用到了二阶导数信息，下面讲解如何用到了二阶导数信息。

二、牛顿法思想

用目标函数的二阶泰勒展开近似该目标函数，通过求解这个二次函数的极小值来求解凸优化的搜索方向。

三、牛顿法推导

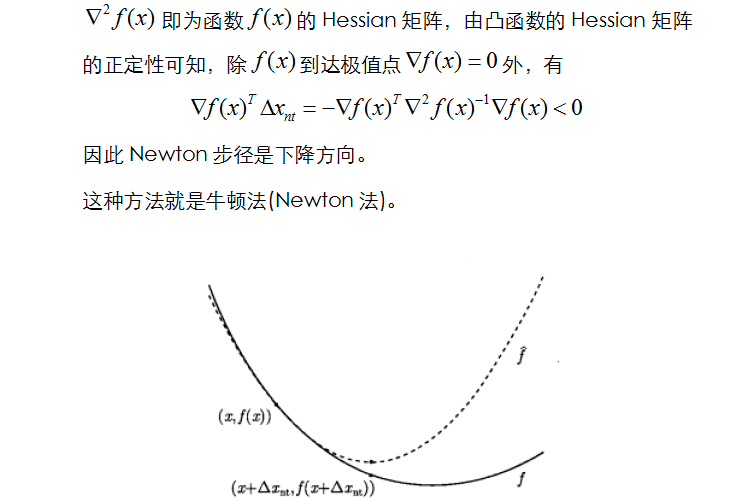
以上推导来自于：凸优化(七)——牛顿法

四、牛顿法和最速梯度下降法的区别

我们可以看出，牛顿法和最速梯度的不同就是在于最速梯度下降法的迭代方向是梯度的负方向，迭代步长根据一维搜索得到。

而牛顿法的迭代方向为上述推导的牛顿步径，迭代步长可以看为定值1。如下：

五、牛顿法的优缺点

1. 优点是：对于二次正定函数，迭代一次即可以得到最优解，对于非二次函数，若函数二次性较强或迭代点已经进入最优点的较小邻域，则收敛速度也很快。
2. 缺点：

• 保证不了迭代方向是下降方向，这就是致命的！先看一个定理：

假设我们认可这个定理：直观理解见下：）

我们判断牛顿法的迭代方向是否朝着函数值下降的方向移动，也就是判断一下迭代方向和 当前点的梯度值做内积，如果小于0就说明是下降方向，我们来计算一下：

迭代方向和当前点的梯度做内积为:

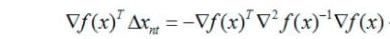
想让它小于0，也就是要求

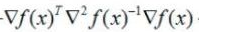
大于0，这恰好是海塞矩阵正定的条件，也就是需要满足当前点的海塞矩阵是正定的，这个要求是很强的，因此并不能保证牛顿法的迭代方向是一定沿着函数值下降的方向。

换句话说就是不一定迭代能够收敛，后面的阻尼牛顿法会解决这个问题，牛顿法就到此为止了。

• 计算量相当复杂，除需计算梯度除外，还需要计算二阶偏导数矩阵和它的逆矩阵，计算量，存储量都很大，并且都以维数N的平方比增加，当N很大的时候，计算量的问题就更加突出。

参考资料：