【射影几何】第四谈——射影变换
前三谈介绍了一些基本的概念,现在我们开始来介绍射影几何中最核心的概念——射影变换
由于本期比较Hard-core,所以各位读者,你品,你细品!

锐腾君个人专栏:https://zhuanlan.zhihu.com/return-mathe01
上期回顾
1.集合的Descartes乘积
2.复元素,共轭复元素
3.圆锥曲线的共轭直径
从中心投影谈起
从圆到圆锥曲线
我们在第一谈中已经介绍了中心投影。我们之前直观地感受过直线在中心投影下的情形,接下来我们来探讨一下圆在中心投影下能够得到的图形。
首先我们需要一个李华(划掉),需要一个中心投影。我们将天蓝色平面上的红色圆通过中心投影到橙色平面(下称为投影平面)上的蓝色轨迹(下称为投影曲线)。我们可以轻易利用Dandelin双球法,验证这个蓝色曲线是个椭圆。
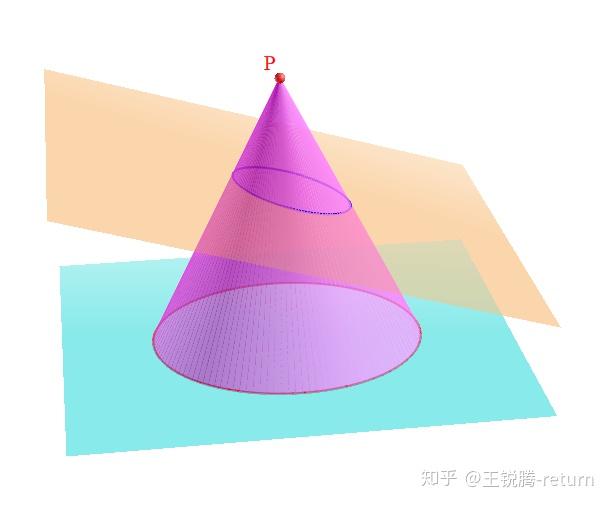
既然在中心投影的角度下,我们能把圆变成椭圆,那么我们何尝不能调整投影平面的“倾斜程度”,将投影曲线变成其他的圆锥曲线呢?

hmmm,一切都是那么地合情合理。所以我们得出结论:圆、椭圆、抛物线、双曲线在射影几何的意义下是一模一样的!
有的读者或许感到迷惑:椭圆明明是条封闭曲线,而双曲线和抛物线都是“敞口”的,何况双曲线还有两个分支,它们怎么可能是完全等价的并且相互可以变换呢?
也许你忘了,我们现在是在谈射影几何。就要在射影平面上看待图形。我们拿双曲线举个例子:


我们将双曲线的两条渐近线,放到射影平面上看,它自然有两个无穷远点。考虑双曲线的极限,它最终会经过 M_\infty,L_\infty 两点。我们将平面上所有的无穷远点构成的直线记为 n_\infty ,那么我们再换一个角度去看这个图形,它大概就是:

这时,我们可以清楚地看到,双曲线的两条渐近线就是它们在无穷远点的切线!
因此,我们在射影平面上辨别一个圆锥曲线是椭圆、抛物线和双曲线的方法,就是看它与无穷远直线的交点数。
定理1:
(1).椭圆与无穷远直线相离,椭圆没有无穷远点
(2).抛物线与无穷远直线相切,抛物线仅有一个无穷远点
(3).双曲线与无穷远直线相交,双曲线有两个无穷远点
当然,我们既然早就引入了无穷远点。那么我们自然也是允许以无穷远点为中心的中心投影的。这一部分内容,且允许我先卖个关子,我们在下一个系列再详细介绍(手动滑稽)。
射影变换——射影几何的核心
射影映射
为了研究中心投影下更多不变的性质,我们需要把中心投影进一步抽象出来。这样我们就需要能够包含中心投影的射影映射。
定义1:通过有限次中心投影,使得射影平面 \pi 变为射影平面 \pi' 的映射叫做射影映射。
我们来举个具体的例子
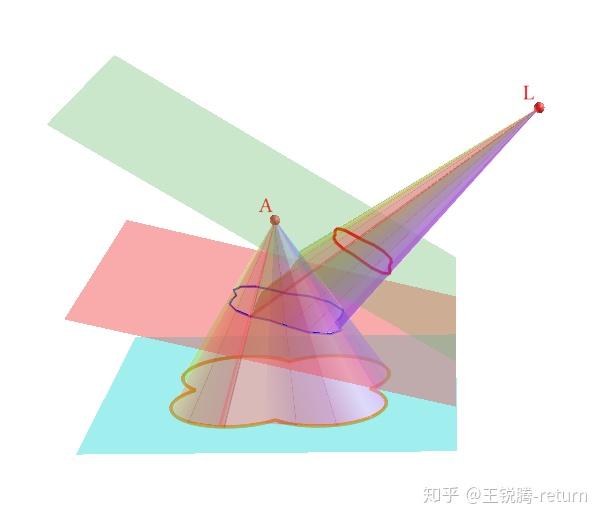
我们将蓝色平面 \pi_{blue} 的菊花状曲线 \Gamma 经过A中心投影,然后再经过L中心投影,得到绿色投影平面 \pi_{green} 上的红色投影曲线 \Gamma' 。我们在这个过程中确定了一个射影映射 f:\pi_{blue}\rightarrow \pi_{green} ,且 f(\Gamma)=\Gamma'
还有一类特殊的射影映射,叫做等距变换(也叫正交变换)。
定义2:等距变换是指不改变任意两点的距离的变换。
我们暂且不加证明地给出如下两个定理(这两个定理我们会在后续文章中给出证明):
定理2:任意一个等距变换总能写成有限个平移变换,旋转变换,镜像变换的复合。
定理3:等距变换是射影映射
射影变换
在此之前,先介绍一下什么是变换。
定义3:若一个映射 f:A\rightarrow A 则称 f 是集合 A 上的变换
如果一个射影映射,是从一个射影平面 \bar\pi 映射到 \bar\pi 。那么这个射影映射就可以称为 \bar\pi 上的射影变换。
我们将下图中绿色平面的图形再绕平面交线旋转回蓝色平面。那么这一系列过程就确定了一个射影变换。

现在我们脱离立体空间,仅仅看一个射影平面。我们在仅仅知道原像和像的情况下,能否唯一确定一个射影变换呢?
事实上,这是肯定可以确定的。只不过是需要原像和像精确到什么程度而已。实际上,4个点就足够了。
定理4:射影平面 \bar\pi 上不存在共线三点的四点 A,B,C,D 分别对应 A',B',C',D' 可以唯一确定一个射影变换。
我们首先证明这样一个射影变换是存在的:

如图,我们将 AB 和 CD 延长,交于点 F ; A'B' 和 C'D' 延长,交于点 F' 。
将 ABCD 留在图形射影平面 \bar\pi 上,而将图形 A'B'C'D' 放到射影平面 \bar\alpha 上。
在空间中,通过移动 \bar\alpha ,将 B' 与 B 重合(这一过程实际上是一个等距变换)。并且我们保证 BF,B'F' 与 \bar\pi,\bar\alpha 的交线 l 仅有一个交点 B(=B') 。
这样一来,其实 BAF,B'A'F' 就大橘已定啦,直接上图!

延长 AA' 和 FF' 交于点 P ,则以 P 为中心的中心投影将 B,A,F 投影为 B',A',F'
这也就是说,将上两步的射影映射一复合,就确定出来了一个将 B,A,F 变换为 B',A',F' 的射影变换啦!
但是,离我们的目标还有一点距离。我们还需要把 C,D 给确定下来。
那么我们不妨设 AB=A'B',AF=A'F' (否则再让上述变换复合一个调整单比的中心投影,然后再复合一步相似变换,这也可以通过等距变换复合中心投影做到),这样一来,我们就可以将图形重新放置在两个平面 \bar\pi_2,\bar\alpha_2 内,而且 A=A',B=B' 保持不动。从而,我们可以再利用一步中心投影,将 C,D 投影为 C',D' 。
我们说明了存在这样的变换,接下来我们来说明这个变换是唯一的:
我们将上面确定出来的变换记为 f ,由于 f 是一个射影变换,那么共线三点被映成共线三点且共线四点交比不变。这是因为中心投影不改变共线四点交比和三点的共线性,而射影变换是一种特殊的射影映射,是有限个中心投影的复合。因此,共线三点仍然被映成共线三点,且共线四点的交比不变。
所以我们现在只需要证明,对于射影平面 \bar\pi 上的任意一点 X ,都会被唯一确定为射影平面 \bar\pi 上的点 X' 。
先考虑一些简单的情形,如果 X 在 AB 边所在的直线上,那么 X'=f(X) 唯一确定。

我们注意到共线四点 B,A,X,F 的交比 (B,A;X,F)=(B'A';X',F')
因此 X' 的位置是唯一的。同理,对于任意其他三条边所在的直线上,也可以证明 X' 唯一确定。
我们再来考虑一般的情形,如果 X 不在四边所在的直线上

我们可以取直线 CX 和 AB 的交点 Y ,它唯一确定了平面上一点 Y'=f(Y) ,类似地,取 BX 和 CD 的交点 Z ,它唯一确定了平面上一点 Z'=f(Z) ,从而 B'Z',C'Y' 的交点 X' 是唯一确定的。
所以上述确定的射影变换 f 是唯一的。
因此,我们简单地可以说,不共线的四点唯一确定一个射影变换。
在定理4的证明中,我们也看到了射影变换不改变点的共线性和共线四点的交比,所以从点共线和交比的角度,更多的数学家喜欢把射影变换叙述成以下形式。
定理5:射影平面上将共线三点映成共线三点,且共线四点的交比不变的变换一定是射影变换。
我们假设这个变换为 f ,取射影平面上的不存在三点共线四点 A,B,C,D 及其四点变换后的像 f(A)=A',f(B)=B',f(C)=C',f(D)=D' 。则这四点唯一确定了一个射影变换 g ,下面我们证明 f=g :
首先,取 AB 和 CD 的交点 F , A'B' 和 C'D' 的交点 F'=g(F) 。则 f(F)=F' ,这是因为 A,B,F 共线 \Rightarrow A',B',f(F) 共线,同理, C',D',f(F) 共线。因此 f(F) 是 A'B',C'D' 的交点,故只能是 F' ,即 f(F)=g(F)\ \ (*)
而对于 AB 上任意一点 Y ,取 f(Y)=Y' ,则 (A,B;Y,F)=(A',B';Y',F')
而注意到 (A',B';g(Y),F')=(A,B;Y,F) ,因此 g(Y)=Y' ,因此 f(Y)=g(Y) ,同样,对于 CD 上的任意一点 Z , f(Z)=g(Z) 。
最后对于平面上任意一点 X ,取 CX 和 AB 的交点 Y , BX 和 CD 的交点 Z ,则 f(Y)=g(Y),f(Z)=g(Z) 。根据 (*) 部分的论述,可以得到 f(X)=g(X)
所以我们也就证明了 f=g
射影等价
如果平面两图形 F,F' 可以通过某射影变换 f 使其相同,即 f(F)=F' ,那么我们就说图形 F 和 F' 射影等价
射影不变量,射影性质——射影几何研究的性质
在这里,我们要提出我们在射影几何中核心要研究的对象——射影不变量和射影性质。
为什么这两者会是我们要核心研究的对象呢?首先我们看一下这两个概念的定义。
定义4:如果图形中的某个量在射影变换下保持不变,则称这个量为射影不变量;图形具有或不具有某个性质(概念)在射影变换后仍然具有或不具有某个性质,则称这个性质为射影性质。
量是一个具体的和数值挂钩的,比如圆锥曲线的离心率,交比等;而性质是一个“是/否”型的,对于一个图形它只有“是”或“不是”两种选择,比如直角,切线等。
这两者在射影几何的地位,就如同角度、距离等概念在平面几何中的地位。
我们在定理4的证明过程中,也注意到了共线四点的交比是射影不变量,共线性(三点共线)是射影性质。
再根据对偶原理,我们也知道共点四线的交比也应当是射影不变量,共点性(三线共点)也是射影性质。
而交比为 -1 又可以称为调和分割,因此调和分割也是一个射影性质。
在文章的开头中,我们也可以说圆锥曲线是个射影性质。
在今后的文章中,我们还会探索更多的射影不变量和射影性质,而射影几何就是围绕着射影变换和射影不变量,射影性质展开的。
大家会不会觉得这一次的文章来的太Hard-core呢?Hard-core的话就需要多一点时间吸收和消化,那是不是代表锐腾君可以咕咕咕一阵子了(滑稽保命)




