高中物理-传送带模型

传送带模型一直以来也算是一个比较复杂的模型了，很多同学也不知道它到底应该怎么去学习。实际上，不管怎么变化，它最本质的东西是不会变的。

传送带模型一共包括三点内容：

• 传送带的动力学问题
• 传送带的能量问题
• 传送带的逻辑推理问题

高中物理的全套视频课程已在B站上持续更新，大家可以搜索“佐木高中物理”收藏观看！

传送带的动力学问题

我们先来说说传送带的动力学问题吧！

为了帮助我们的学习，我们先把动力学问题分为四种情况：

• 同向无外力
• 异向无外力
• 同向有外力
• 异向有外力

若滑块滑上传送带时的速度与传送带的速度方向相同，则称为同向；反之则为异向。

若只有滑动摩擦力给滑块提供加速度时，则称为无外力；反之称为有外力。滑动摩擦力之外的力都叫外力。简单来说：无外力的情况只能出现在水平传送带上。

同向无外力时：滑块最多只能出现五种运动情况：

• 一直匀加速运动
• 先匀加速，共速之后匀速运动
• 一直匀速运动（ v_1=v_2 ）
• 一直匀减速运动
• 先匀减速，共速之后匀速运动

而且在这五种情况里面，“一直匀速运动”这种情况在高考中几乎不会出现，所以只需要把另外四种情况学习清楚就好了。

1．如图所示为一水平传送带装置示意图，绷紧的传送带始终保持恒定的速率v=4m/s运行，将滑块无初速度地放在左端点A处。传送带A、B间的距离为L=16m，滑块与传送带间的动摩擦因数 \mu=0.2 。则

（1）滑块在传送带上运动了多长时间？

（2）若滑块以初速度 v_0=10m/s 从A点进入传送带，则滑块在传送带上运动多少时间？

解析：(1)因为滑块无初速度地放在左端点A处，所以滑块先在传送带上做匀加速运动

\mu mg=ma

∴a=2m/s^2

滑块与传送带共速的时间 t_1=\frac{v}{a}=\frac{4}{2}=2s

滑块与传送带共速时的位移 x_1=\frac{1}{2}at^2=\frac{1}{2}\times2\times2^2=4m

∵ x_1<L

∴滑块与传送带共速时，滑块还在传送带上。共速后，滑块继续向前做匀速运动

L-x_1=vt_2

∴ t_2=3s

所以滑块在传送带上运动的时间 t=t_1+t_2=5s

(2)因为滑块的初速度大于传送带的速度，所以滑块先在传送带上做匀减速运动

\mu mg=ma

∴a=2m/s^2

滑块与传送带共速的时间 t_1=\frac{v_0-v}{a}=\frac{10-4}{2}=3s

滑块与传送带共速时的位移 x_1=v_0t_1-\frac{1}{2}at_1^2=10\times3-\frac{1}{2}\times2\times3^2=21m

∵ x_1>L

∴滑块与传送带共速之前，滑块就已经离开传送带了，则滑块在传送带上一直做匀减速运动。

设滑块在传送带上运动的时间为t，则

L=v_0t-\frac{1}{2}at^2

∴t=2s

注意：同向传送带，一定要判断滑块能不能与传送带共速（这一点极其关键，也是很多同学会忘的一点）

异向无外力：

设滑块滑上传送带时的速度为 v_1 ，传送带的速度为 v_2 ，传送带的长度为 L ，物块的速度减为0时的位移为 x_1 ，所花的时间为 t_1 。

异向无外力时：滑块在传送带上最多只能出现三种运动情况：

• 一直匀减速运动
• 先匀减速运动，然后反向一直匀加速运动
• 先匀减速运动，然后反向先做匀加速运动，与传送带共速后再做匀速运动

我编写的《高中物理知识模型探究与实践》一书里面专门针对受力分析、牛顿第二定律、传送带和滑块木板、平抛运动、圆周运动、天体运动、动能定理功能关系和动量的基本知识点和基本模型进行了全面细致地讲解，采用的是讲解式的叙述手法。在阅读这本书的时候，仿佛有一个虚拟的物理老师在带着大家进行学习一样，不用担心阅读困难，知识点看不懂。

在下方这个百度网盘的链接中有这本物理资料的电子档，需要的同学可以下载下来进来学习！

链接：https://pan.baidu.com/s/1n8_4BOOxNNITZShoCbBP6A?pwd=bzax

模型分析：

异向传送带时，由于滑块的运动方向与传送带的运动方向相反，则滑块有可能会从另一边离开传送带。因此只要遇到异向传送带问题，首先需要分析的就是滑块会不会从另一边离开传送带。分析方法如下：

第一步：求出滑块的加速度： \mu mg=ma

第二步：求出滑块速度减为0的时间： t_1=\frac{v_1}{a}

第三步：求出滑块速度减为0时的位移： x_1=\frac{v_1+0}{2}\cdot t_1=\frac{v_1^2}{2\mu g}

如果 x_1>L (L为传送带的长度)，则滑块会从另一边离开传送带；

如果 x_1<L (L为传送带的长度)，则滑块不会从另一边离开传送带。

从上面第三步最终得到的表达式与L作比较来看，滑块能不能从另一端离开传送带只与滑块滑上传送时的速度 v_1 、动摩擦因数 \mu 和传送带的长度L有关，与传送带的速度无关。

那么是否可以得到一些推论：如果滑块能够从传送带的另一边离开传送带，那么不管传送带的速度 v_2 变大还是变小，滑块还是能够从传送带的另一边离开传送带。这是异向无外力传送带的二级结论之一。

如果滑块能从另一端离开传送带，则滑块离开传送带时的速度，在传送带上运动的时间又有什么特点呢？

我们把求这两个物理量的公式写出来看一下，能不能有一些重大发现呢？

滑块离开传送带时的速度： v^2-v_1^2=-2\cdot\mu g\cdot L

滑块在传送带上运动的时间： L=v_1t-\frac{1}{2}at^2=v_1t-\frac{1}{2}\cdot\mu g\cdot t^2

从这两个式子中，我们发现这两个物理量与传送带的速度也没有任何关系。

那我们是不是就有可以这样理解：滑块能不能从另一端离开传送带，以及从另一端离开传送带时的速度和滑块在传送带上运动的时间，只与滑块滑上传送时的速度 v_1 、动摩擦因数 \mu和传送带的长度L有关，与传送带的速度无关。

我们也可以这样理解：如果滑块能够从传送带的另一边离开传送带，那么不管传送带的速度 v_2 变大还是变小，滑块还是能够从传送带的另一边离开传送带，并且滑块从另一端离开传送带的速度，以及滑块在传送带上运动的时间不变。

如果滑块速度减为0时没有从另一端离开传送带，那么滑块返回时又会做什么运动呢？

当滑块返回时，相当于是初速度为0的同向传送带模型，而同向传送带模型的关键是判断滑块与传送带能否共速。那么我们现在就来分析分析滑块在什么情况下能和传送带共速，什么情况下不能和传送带共速。

还是一样的分析方式：

滑块的加速度： \mu mg=ma

滑块与传送带共速的时间 t_2=\frac{v_2}{a}

滑块与传送带共速时的位移 x_2=\frac{1}{2}at_2^2

如果 x_2\geq x_1 ：则滑块返回时不能与传送带共速，滑块返回时一直做匀加速运动；

如果 x_2< x_1 ：则滑块返回时能与传送带共速，滑块返回时先做匀加速运动，与传送带共速后做匀速运动。

上面的分析方式就有点中规中矩了，这种写法是做计算题的方式。其实对于做选择题或者想要快速分析的话，还是得掌握好一个基本推论，也就是我们所说的二级结论。

一说到二级结论，那么我们就得要谈到匀变速直线运动的对称性原则了。

所谓匀变速直线运动的对称性原则，就是如果一个物体对匀减速运动和反向做匀加速运动的加速度相同，则

• 当这个物体经过同一位置的时候，这个物体的速度的大小相等；
• 当这个物体经过同一段距离的时候，这个物体所花的时间相同。

例如上图所示，滑块向左做匀减速运动，速度减为0后再返回做匀加速运动，而匀减速运动和匀加速运动的加速度相同，则滑块经过同一点A时的速度大小一定相等，经过同一点B时的速度大小也一定相等。而滑块向左做匀减速运动经过AB段的时间与向右做匀加速运动经过AB段的时间也一定相同。这就是匀变速直线运动的对称性原则。

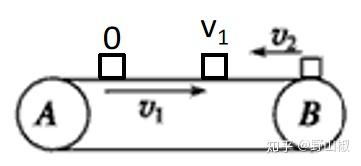
（注意 ：在这个图中，传送带的速度为 v_1 ，滑块的速度为 v_2 ，和之前的不一样，不要弄错了。）

而在异向传送带中，当滑块速度减为0后返回时，滑块的加速度和之前做匀减速运动的加速度完全相同。根据匀变速直线运动的对称性原则，如果 v_1<v_2 ，则滑块还没有返回最右端时（如上图），滑块的速度就已经和传送带达到共速。当然如果 v_1>v_2 ，则滑块到达传送带右端时速度大小为 v_2 ，还没有共速。如果 v_1=v_2 ，则滑块刚好加到最右端时与传送带共速。

则根据上述分析，我们又可以得到结论如下：

• 如果 v_1<v_2 ：滑块返回时一定先做匀加速运动，与传送带共速后做匀速运动；
• 如果 v_1\geq v_2 ：滑块返回时一直做匀加速运动。

这是滑块不能从传送带另一端离开传送带，返向运动时，滑块的运动过程的快速分析方法。这个方法可以让分析的速度加快，但是计算题的解题步骤一定不能这样写，计算题还是要按照标准的解题步骤来写。

上述的内容就是异向传送带的基本模型。接下来给一个例题，实际地来做一做。

2．如图，水平传送带以 v_1=4m/s 速度顺时针方向运行。现有一质量m=0.4kg的小物块（可视为质点），以 v_2=6m/s 水平速度向左滑上传送带。已知小物块与传送带的动摩擦因数μ= 0.5，滑动摩擦力等于最大静摩擦力，传送带两转轴间的距离 l=5m ，取 g=10m/s^2 ，sin 37°= 0.6，cos37°= 0.8。求：小物块从滑上传送带至离开传送带的过程中所经历的时间。

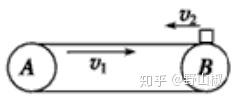
注意：这个题我们一定要先分析滑块会不会从左端离开传送带，如果滑块不会从左端离开传送带，则一定要分析滑块返回时能不能共速。因为 v_1<v_2 ，所以滑块返回时一定先做匀加速运动，共速后再做匀速运动。不过我们解题的时候一定不要这样写，必须按照标准写法来写。

解析：

\mu mg=ma

∴a=5m/s^2

滑块速度减为0的时间 t_1=\frac{v_2}{a}=1.2s

滑块速度减为0时的位移 x_1=\frac{v_2+0}{2}\cdot t_1=3.6m

∵ x_1<l

∴滑块不会从左端离开传送带

滑块反向做匀加速运动到达共速的时间 t_2=\frac{v_1}{a}=0.8s

滑块反向做匀加速运动到达共速的位移 x_2=\frac{1}{2}at_2^2=\frac{1}{2}\times5\times0.8^2=1.6m

∵ x_2<x_1

∴滑块反向运动时，先做匀加速运动，然后再做匀速运动

x_1-x_2=v_1t_3

∴ t_3=0.5s

滑块在传送带上运动的时间 t=t_1+t_2+t_3=2.5s

接下来是有外力传送带。

有外力传送带相对而言比较复杂。那么首先，什么是有外力传送带？

当我们写牛顿第二定律的时候，如果除了摩擦力之外还有其他的力，那么就称为有外力。摩擦力之外的所有力都叫外力。比如：我们写了一个牛顿第二定律式子 mgsin\theta-\mu mgcos\theta=ma ，此时就是有外力传送带，而 mgsin\theta 就是外力。

倾斜传送带就是典型的有外力传送带，水平传送带也有可能出现有外力的时候。

我以倾斜传送带举来说明有外力传送带应该怎么去分析。一旦我们遇到倾斜传送带，如果是同向传送带，同样要分析共速的时候滑块还在不在传送带上；如果是异向传送带，也同样要分析滑块会不会从另一边离开传送带。

不过倾斜传送带的分析方式和水平传送带区别还是挺大的。下面我以几个例题来给大家说明倾斜传送带应该怎么分析。

3．如图所示，倾角为 \theta=37^o ，长为 l=16m 的传送带，转动速度为v＝10 m/s，动摩擦因数μ＝0.5，在传送带顶端A处无初速度地释放一个质量为m＝1 kg的物体．已知sin 37°＝0.6，cos 37°＝0.8， g=10m/s^2 .求：

(1)传送带顺时针转动时，物体从顶端A滑到底端B的时间；

(2)传送带逆时针转动时，物体从顶端A滑到底端B的时间．

解析：（1）因为传送带顺时针转运，而滑块往下运动，所以是异向传送带

∵ mgsin\theta-\mu mgcos\theta=ma

∴ a=2m/s^2

滑块往下做匀加速运动，滑块只能从B端离开传送带。

l=\frac{1}{2}at^2

∴ t=4s

（2）因为传送带逆时针转运，而滑块往下运动，所以是同向传送带

而同向传送带一定要分析滑块能否和传送带共速，分析方式和水平传送带完全一样

∵ mgsin\theta+\mu mgcos\theta=ma_1 (因为滑块相对传送带向上运动，所以滑块所受的摩擦力向下。滑动摩擦力的方向与相对运动的方向相反，这是很多同学很容易错的一点)

∴ a_1=10m/s^2

滑块与传送带共速的时间 t_1=\frac{v}{a_1}=\frac{10}{10}=1s

滑块与传送带共速时的位移 x_1=\frac{1}{2}a_1t_1^2=\frac{1}{2}\times10\times1^2=5m

∵ x_1<l

∴滑块与传送带共速的时候，滑块还在传送带上

注意：很多同学认为滑块与传送带共速之后，滑块就与传送带一起做匀速运动。所以很多同学一遇到倾斜传送带，出错的概率就大大地增加。其时因为重力分力的关系，滑块与传送带共速之后不一定做匀速直线运动，这一点与水平传送带不一样。所以倾斜传送带的重点就在于共速之后滑块到底做什么运动。

共速之后，首先需要分析的就是摩擦力的方向问题。这一点也是困扰很多同学的一个因素。其时不管共速之前摩擦力向哪个方向，共速之后，摩擦力的方向一定与外力的方向相反。这是一个重点。

所以在这个题的这种情况下，因为外力 mgsin\theta 的方向向下，则共速之后，滑块所受的摩擦力方向一定向上。

而共速之后滑块到底做什么运动，可以利用一些口诀来分析。

• 加速达到共速，共速之后不可能减速；
• 减速达到共速，共速之后不可能加速。

意思就是如果共速之前，滑块做的是匀加速运动，则共速之后要么继续匀加速运动，要么做匀速运动，反正不可能做匀减速运动；同样如果共速之前，滑块做的是匀减速运动，则共速之后要么继续匀减速运动，要么做匀速运动，反正不可能做匀加速运动。

注意：这个点必须要外力的大小和方向一直不发生变化的情况下才适用。

但是光靠上面这两句话只能是缩小范围，而不能真正地分析出来。所以还要加上另外一句话，就是共速之后加速度的方向一定跟摩擦力的方向相反。这几个点结合起来，就能够分析出共速之后，滑块到底会做什么运动了。

那么在这个问的情况下，滑块与传送带共速之后，由于外力的方向向下，所以摩擦力的方向向上。（倾斜传送带，共速之后，摩擦力的方向几乎都是向上的，只要除了重力分力这个外力之外没有其他的外力）

根据牛顿第二定律，可得

mgsin\theta-\mu mgcos\theta=ma_2

∴ a_2=2m/s^2

共速之后，加速度的方向向下，与摩擦力的方向确实相反，所以此加速度成立，则滑块在共速之后继续向下做匀加速运动。

l-x_1=vt_2+\frac{1}{2}a_2t_2^2

∴ t_2=1s

∴滑块在传送带上总的运动时间 t=t_1+t_2=1+1=2s

在考试的时候，如果遇到这种题，可以不用写这么多。到时的解题步骤可以写成下面这样

（2）∵ mgsin\theta+\mu mgcos\theta=ma_1

∴ a_1=10m/s^2

滑块与传送带共速的时间 t_1=\frac{v}{a_1}=\frac{10}{10}=1s

滑块与传送带共速时的位移 x_1=\frac{1}{2}a_1t_1^2=\frac{1}{2}\times10\times1^2=5m

∵ x_1<l

∴滑块与传送带共速的时候，滑块还在传送带上

∵ mgsin\theta >\mu mgcos\theta

∴滑块与传送带共速之后，滑块继续向下做匀加速运动

mgsin\theta-\mu mgcos\theta=ma_2

∴ a_2=2m/s^2

l-x_1=vt_2+\frac{1}{2}a_2t_2^2

∴ t_2=1s

∴滑块在传送带上总的运动时间 t=t_1+t_2=1+1=2s

我建立了一个Q裙：一三五四五二八二五，专门用于高中物理的学习交流，我会在每晚9点到11点之间在裙里面进行答疑解惑，欢迎大家进裙交流学习！

上面就是倾斜传送带的完整的分析方式。如果遇到水平传送带也带外力的情况，分析方式和这个分析方式几乎完全一样。

接下来我们再举两个比较常见的例子来说明有外力传送带的分析过程。

4．如图所示为一以 v_2=4m/s 的速度顺时针转动的倾斜传送带，传送带AB两端相距 l=5.4m ，传送带与地面倾角 \theta=37^o 。一个质量为 m=10kg 的物块以初速度 v_1=8m/s 滑上传送带，物块与传送带间的动摩擦因数为0.5。求：物块在传送带上运动的时间？

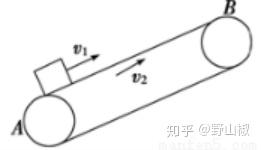
解析：因为滑块的速度比传送带的速度大，所以滑块相对传送带向上运动，则滑块在传送带上运动时所受的滑动摩擦力向下

mgsin\theta+\mu mgcos\theta=ma_1

∴ a_1=10m/s^2

滑块与传送带共速的时间 t_1=\frac{v_1-v_2}{a_1}=\frac{8-4}{10}=0.4s

滑块与传送带共速时的位移 x_1=\frac{v_1+v_2}{2}\cdot t_1=\frac{8+4}{2}\times0.4=2.4m

∵ x_1<l

∴滑块与传送带共速的时候，滑块还在传送带上

∵ mgsin\theta >\mu mgcos\theta

∴滑块与传送带共速之后，滑块继续向上做匀减速运动

mgsin\theta-\mu mgcos\theta=ma_2

∴ a_2=2m/s^2

滑块从共速到速度减为0运动的位移 x_2=\frac{v_2^2-0}{2a_2}=4m

∵ x_2>l-x_1

∴滑块能从传送带上端离开传送带

则 l-x_1=v_2t_2-\frac{1}{2}a_2t_2^2

∴ t_2=1s

∴滑块在传送带上总的运动时间 t=t_1+t_2=0.4+1=1.4s

注意：如果滑块没有从上端离开传送带，那么又该怎么分析呢？

5．如图所示，传送带与水平面之间的夹角 \theta=30^o ，其上A、B两点间的距离 l=5m ，传送带在电动机的带动下以 v=1m/s 的速度匀速运动。现将一质量 m=10kg 的小物体（可视为质点）轻放在传送带的A点，已知小物体与传送之间的动摩擦因数 \mu=\frac{\sqrt{3}}{2} ，在传送带将小物体从A点传送到B点的过程中（取 g=10m/s^2 ），求：物体从A到B运动的时间？

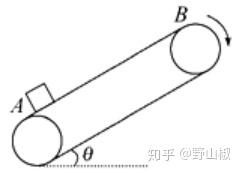
解析：因为滑块的初速度为0，所以滑块相对传送带向下运动，则滑块在传送带上运动时所受的滑动摩擦力向上

\mu mgcos\theta-mgsin\theta=ma

∴ a=2.5m/s^2

滑块与传送带共速的时间 t_1=\frac{v}{a}=\frac{1}{2.5}=0.4s

滑块与传送带共速时的位移 x_1=\frac{v+0}{2}\cdot t_1=\frac{1+0}{2}\times0.4=0.2m

∵ x_1<l

∴滑块与传送带共速的时候，滑块还在传送带上

∵ mgsin\theta <\mu mgcos\theta

∴滑块与传送带共速之后，滑块向上做匀速运动（因为共速之后，加速度方向与摩擦力方向相同，所以加速度不存在）

l-x_1=vt_2

∴ t_2=4.8s

∴滑块在传送带上总的运动时间 t=t_1+t_2=0.4+4.8=5.2s

传送带的动力学问题到这儿也就基本上结束了，不过在讲解传送带的能量问题之前，我们先解决一下相对位移\Delta x 、滑痕的长度d和摩擦生热Q的大小问题。

摩擦生热问题其实是属于能量问题，但是因为知识的结构性，所以我们把它和相对位移一起讲。

滑块与传送带的相对位移 \Delta x ：（设滑块的初速度为 v_1 ，传送带的速度为 v_2 ）

同向传送带：

\Delta x=\left| x_滑-x_传 \right|

异向传送带：

若 v_1>v_2 ： \Delta x= x_滑+x_传 ；

若 v_1\leq v_2 ： \Delta x= x_传 。

另外还有一种情况极其特殊，遇到的概率极其小，所以在这里就不讲了。用上面的内容求相对位移 \Delta x 已经完全够用了。

滑痕的长度d：
在不重复滑的情况下，滑痕的长度d就等于相对位移 \Delta x 的大小。
摩擦生热Q：
Q=f\cdot\Delta x


6．如图所示为一水平传送带装置示意图，绷紧的传送带始终保持恒定的速率v=4m/s运行，将滑块无初速度地放在左端点A处。传送带A、B间的距离为L=16m，滑块与传送带间的动摩擦因数 \mu=0.2 。则

（1）滑块在传送带上运动了多长时间？
（2）若滑块以初速度 v_0=10m/s 从A点进入传送带，则滑块在传送带上运动多少时间？
（3）若滑块和传送带相对滑动时会在传送带上留下滑痕，则在第（2）问的条件下滑痕的长度是多少？
解析：第(1)问和第(2)问的解析过程请观看前方第1题，这里为了节省篇幅，所以就省略了。
(3)滑块的对地位移 x_滑=L=16m
传送带的对地位移 x_传=vt=4\times2=8m
因为滑块与传送带的速度同向，并且没有重复滑动，所以
滑痕的长度d=\Delta x=x_滑-x_传=16-8=8m


7．如图，水平传送带以 v_1=4m/s 速度顺时针方向运行。现有一质量m=0.4kg的小物块（可视为质点），以 v_2=6m/s 水平速度向左滑上传送带。已知小物块与传送带的动摩擦因数μ= 0.5，滑动摩擦力等于最大静摩擦力，传送带两转轴间的距离 l=5m ，取 g=10m/s^2 ，sin 37°= 0.6，cos37°= 0.8。求：
（1）小物块从滑上传送带至离开传送带的过程中所经历的时间。
（2）小物块从滑上传送带至离开传送带的过程中相对传送带右端B点运动的最大距离。
（3）小物块从滑上传送带至离开传送带的过程中相对传送带运动的最大距离。

解析：第(1)问的解析过程请观看前方第2题，这里就不再多赘述了。
(2)这个问题问的是滑块在运动过程中相对传送带右端B点运动的最大距离。重点在右端B点，所以这个问问的是对地位移，不是相对位移。此时就需要用到一个小知识点了，就是速度为0时，对地位移最大；共速时，相对位移最大。
所以这个问问的就是当滑块向左做匀减速运动，当滑块速度减为0时的对地位移是多少。由第(1)问可知，滑块相对传送带右端B点的最大距离 d_{max}=x_1=3.6m
(3)这个问题问的是滑块在运动过程中相对传送带的最大距离，意思就是求的是相对位移 \Delta x 的最大值。由速度为0时，对地位移最大；共速时，相对位移最大。可知，当滑块与传送带共速时，相对位移最大。
由第一问的结果可知：当滑块与传送带共速时，
滑块的对地位移 x_滑=x_1-x_2=3.6-1.6=2m
传送带的对地位移 x_传=v_1(t_1+t_2)=4\times(1.2+0.8)=8m
因为是异向传送带，并且滑块的初速度大于传送带的速度，则
共速时滑块与传送带的相对位移为 \Delta x=x_滑+x_传=2+8=10m


从前面两个例题来看，给人的感觉就是好像这三个考点一点都不难，挺简单的。确实是这样子的，本来这些考点难度就不大。但是如果不知道下面的这种情况的话，那么就为以后考试丢分埋下了伏笔。大家当然不希望自己丢分，所以接下来的这个例题一定要好好地看看！


8．如图所示，倾角为 \theta=37^o ，长为 l=16m 的传送带，转动速度为v＝10 m/s，动摩擦因数μ＝0.5，在传送带顶端A处无初速度地释放一个质量为m＝1 kg的物体．已知sin 37°＝0.6，cos 37°＝0.8， g=10m/s^2 .求：
(1)传送带顺时针转动时，物体从顶端A滑到底端B的时间；
(2)传送带逆时针转动时，物体从顶端A滑到底端B的时间；
(3)在第（2）问的条件下，物体与传送带间的相对位移，滑痕的长度及产生的热量．

解析：第(1)问和第(2)问的解析过程请观看前方第3题，这里也就不再多赘述了。
(3)由于滑块从A滑到B，所以滑块的对地位移 x_滑=l=16m
传送带的对地位移 x_传=vt=10\times2=20m
因为是同向传送带，所以相对位移 \Delta x=x_传-x_滑=20-16=4m
滑痕的长度 d=\Delta x=4m
摩擦产生的热量 Q=f\cdot\Delta x=\mu mgcos\theta\cdot\Delta x=16J


注意：上面的解题过程，很多同学都会认为是正确的。其时除了相对位移之外，其他的全是错的，而这一点就是很多同学不清楚的地方。
因为这个题出现了之前的例题都没有出现的情况，就是滑块与传送带发生了重复滑的问题。所以导致了滑痕的长度不等于相对位移的大小，摩擦生热的计算也不应该直接用相对位移来算。
那么正确的解题过程又应该是什么样的呢？
我们从第(2)问的解题过程了解到，滑块与传送带之间的运动分为两段运动过程。第一段是共速之前，第二段是共速之后。
在滑块与传送带共速之前，滑块相对传送带向上运动。所以在第一段运动过程中，滑块与传送带的相对位移 \Delta x_1=x_{传1}-x_{滑1}=vt_1-x_1=10\times1-5=5m ，此时滑痕的长度已经等于5m，自然前面计算的4m肯定是错的。
而在滑块与传送带共速之后，滑块继续向下做匀加速运动，滑块相对传送带往下滑。所以在第二段运动过程中，滑块与传送带的相对位移 \Delta x_2=x_{滑2}-x_{传2}=(l-x_1)-vt_2=(16-5)-10\times1=1m。所以总的相对位移 \Delta x=\Delta x_1-\Delta x_2=5-1=4m ，而滑痕的长度d只能等于 \Delta x_1=5m ，因为共速之后是对原先的5m的上面重复滑了1m，重复滑的情况下，滑痕的长度不会变长。
虽然两次重复滑动，但是两次滑动都会产生热量。所以摩擦产生的热量应该把两次摩擦产生的热量都算进去。摩擦生热的大小 Q=f\cdot(\Delta x_1+\Delta x_2)=24J。
第(3)问的正确解法应该如下所示：
(3)由于滑块从A滑到B，所以滑块的对地位移 x_滑=l=16m
传送带的对地位移 x_传=vt=10\times2=20m
因为是同向传送带，所以相对位移 \Delta x=x_传-x_滑=20-16=4m
在共速之前： \Delta x_1=x_{传1}-x_{滑1}=vt_1-x_1=10\times1-5=5m
在共速之后： \Delta x_2=x_{滑2}-x_{传2}=(l-x_1)-vt_2=(16-5)-10\times1=1m
滑痕的长度 d=\Delta x_1=5m
摩擦产生的热量 Q=f\cdot(\Delta x_1+\Delta x_2)=\mu mgcos\theta\cdot(\Delta x_1+\Delta x_2)=24J


上面的例题才是这三个考点最核心的东西。只有把这个最核心的东西学明白，在考试中就算遇到了才不会怕。
接下来我们正式进入传送带的能量问题。

传送带的能量问题

摩擦力对滑块对的功：

• W_滑=f\cdot x_滑 ( x_滑 为滑块的对地位移)；
• 对滑块用动能定理。

因传送滑块电动机做的功等于消耗的电能：

• W_传=\Delta E_电=f\cdot x_传( x_传 为传送带的对地位移)；
• 能量守恒定律： \Delta E_电=\Delta E_k+\Delta E_p+Q 。( \Delta E_k 为滑块增加的动能， \Delta E_p 为滑块增加的重力势能，Q为摩擦产生的热量)

接下来我们就以一个例题来讲解一下，这几个公式的用法。

9．如图所示，传送带与水平面之间的夹角 \theta=30^o ，其上A、B两点间的距离 l=5m ，传送带在电动机的带动下以 v=1m/s 的速度匀速运动。现将一质量 m=10kg 的小物体（可视为质点）轻放在传送带的A点，已知小物体与传送之间的动摩擦因数 \mu=\frac{\sqrt{3}}{2} ，在传送带将小物体从A点传送到B点的过程中（取 g=10m/s^2 ），求：
（1）物体从A到B运动的时间？
（2）传送带对小物体做的功；
（3）电动机做的功．

解析：(1)因为滑块的初速度为0，所以滑块相对传送带向下运动，则滑块在传送带上运动时所受的滑动摩擦力向上
\mu mgcos\theta-mgsin\theta=ma
∴ a=2.5m/s^2
滑块与传送带共速的时间 t_1=\frac{v}{a}=\frac{1}{2.5}=0.4s
滑块与传送带共速时的位移 x_1=\frac{v+0}{2}\cdot t_1=\frac{1+0}{2}\times0.4=0.2m
∵ x_1<l
∴滑块与传送带共速的时候，滑块还在传送带上
∵ mgsin\theta <\mu mgcos\theta
∴滑块与传送带共速之后，滑块向上做匀速运动（因为共速之后，加速度方向与摩擦力方向相同，所以加速度不存在）
l-x_1=vt_2
∴ t_2=4.8s
∴滑块在传送带上总的运动时间 t=t_1+t_2=0.4+4.8=5.2s
(2)
第一种解法：基本公式法
从第(1)问可知：滑块在传送带上运动的过程中，共速之前滑块受到的是滑动摩擦力，方向向上；共速之后，滑块受到的是静摩擦力，方向也向上。
而滑块的运动方向也向上，所以滑块在整个运动过程中，摩擦力对滑块做的都是正功。
∴ W_滑=f_滑\cdot x_1+f_静\cdot(l-x_1)=\mu mgcos\theta\cdot x_1+mgsin\theta\cdot (l-x_1)=255J
第二种解法：动能定理
W_滑-mg\cdot lsin\theta=\frac{1}{2}mv^2-0
∴ W_滑=255J
(3)
第一种解法：基本公式法
电动机做的功就等于摩擦力对传送带做的功。
∴ W_传=f_滑\cdot vt_1+f_静\cdot vt_2=\mu mgcos\theta\cdot vt_1+mgsin\theta\cdot vt_2=270J
第二种解法：能量守恒定律
W_传=\Delta E_电=\Delta E_k+\Delta E_p+Q=\frac{1}{2}mv^2+mg\cdot lsin\theta
+\mu mgcos\theta\cdot(vt_1-x_1)=270J


传送带的动力学问题和能量问题中的两大特殊案例：

（1）每隔相同的时间T向传送带上静止释放一个工件，共速后每相邻的两个工件的距离为L，传送带的速度为v，则一定满足： L=vT 。

证明：设第一个工件在传送带上运动的时间为t，则第二个工件在传送带上运动的时间为t-T。

第一个工件在传送带上运动的位移 x_1=\frac{0+v}{2}\cdot t_1+v(t-t_1)

第二个工件在传送带上运动的位移x_2=\frac{0+v}{2}\cdot t_1+v(t-T-t_1)

当两个工件在传送带上都与传送带共速之后，两个工件之间的距离为L，则

L=x_1-x_2=vT 。

这个结论在条件满足的情况下都是可以直接用的，在做选择题的时候特别好用。

它满足的前提条件就是工件在传送带上必须先做匀加速运动，共速之后再做匀速运动。

（2）若满足①滑块的速度从0到共速②必须是水平传送带，则 Q=\frac{1}{2}mv^2 、 \Delta E_电=mv^2 。

证明：滑块的速度从0加速到共速，则滑块的位移 x_1=\frac{0+v}{2}\cdot t=\frac{vt}{2}

传送带的位移 x_2=vt

则 x_2=2x_1

在整个过程中对滑块用动能定理，得

f\cdot x_1=\frac{1}{2}mv^2-0

而摩擦产生的热量 Q=f\cdot\Delta x=f\cdot(x_2-x_1)=f\cdot x_1

所以摩擦产生的热量 Q=\frac{1}{2}mv^2

传送带因传送滑块多消耗的电能 \Delta E_电=\Delta E_k+Q=\frac{1}{2}mv^2+\frac{1}{2}mv^2=mv^2

可能会存在的疑问：

1.为什么滑块的速度必须从0加速到共速？

因为如果滑块的速度不是从0加速到共速的话，那么 x_2\ne 2x_1 ，这个时候摩擦产生的热量Q也就不等于 f\cdot x_1 ，结论不成立。

2.为什么必须是水平传送带，倾斜传送带为什么不行？

因为如果是倾斜传送带的话，对滑块用动能定理的时候就会出现重力做功

f\cdot x_1+mg\cdot lsin\theta =\frac{1}{2}mv^2-0，也无法得出上述结论。

10．如图所示，水平传送带以恒定速率传动．每隔相同时间T，在左端A点，轻轻放上一个完全相同的工件，已知工件与传送带之间的动摩擦因数为μ，工件质量为m．经测量，发现那些已经和传送带共速的工件之间的距离均为L．已知重力加速度为g，下列说法正确的是（ ）

A. 传送带的速度大小为 \frac{L}{T}

B. 工件在传送带上加速时间为 \frac{L}{2T\mu g}

C. 每个工件与传送带间因摩擦而产生的热量为 \frac{\mu mgL}{2}

D. 传送带因传送每一个工件而多消耗的能量为 \frac{mL^2}{T^2}

解析：这个题完全适用于上述结论，水平传送带，滑块的速度从0增加到共速，每隔相同时间T放一个完全相同的工件。

直接套用前面的结论，就可以得出传送带的速度 v=\frac{L}{T} ，而传送带因传送每一个工件多消耗的能量 \Delta E_电=mv^2=\frac{mL^2}{T^2}，所以选项A和选项D是正确的。

工件在传送带上的加速时间 t=\frac{v}{a}=\frac{v}{\mu g}=\frac{L}{T\mu g} ，所以选项B是错误的，多了一个数字2

每个工件与传送带间因摩擦而产生的热量 Q=f\cdot \Delta x=\mu mg\cdot\Delta x， 而相对位移 \Delta x=x_1=\frac{1}{2}vt （t为工件的速度从0加速到与传送带共速的时间），而 L=vT ，所以只有当 t=T 时，选项C才是正确的，所以这个题C选项错误。

经过分析，这个题的最终答案为AD。

传送带的能量问题到这里也就结束了，后面我会在新的一篇文章里面更新传送带的逻辑推理的问题，有兴趣的朋友可以关注我的新文章哈！