《算法导论》阅读总结

(原来知乎限制了导入文档大小为5MB)

写作目标：

1. 整体掌握《算法导论》所有内容，结构化知识网络；
2. 把重点知识讲得浅显易懂；
3. 提出一些独到的见解；
4. 能非常流畅地给别人讲解本书重点内容；

写作手法：

1. 头脑风暴，快速回顾，整体打个草稿；
2. 重新读一遍，细嚼慢咽；查阅资料；用python写算法；

相关资料：

1.MIT《算法导论》公开课：http://open.163.com/newview/movie/free?pid=M6UTT5U0I&mid=M6V2T1JGF

前言 题外话

个人感受。我是一个非科班出生的转行程序员，每次出去面试时最怕做笔试题，尤其是算法相关的题目，好多连名字都没听说过。以前听到别人说二叉树、堆排序、B+树、时间复杂度大O等，我都觉得高大上，觉得这些概念就是神一样的存在。我已经有三年半的工作经验了，而且自认为我是个勤奋而又有天赋的程序员，这三年来看了20本左右编程经典书籍，比如：《unix环境高级编程》、《windows核心编程》、《TCP/IP协议》、《GOF设计模式》、《深入linux内核架构》、《MYSQL技术内幕》、《系统架构》，自认为水平已经很牛逼，还常以高级工程师自居；然而一线IT公司面试笔试必考算法，我就心虚了，总感觉自己的完备的技术栈缺了点啥；今年我又准备跳槽，想去优秀的IT大公司，比如华为、海康威视、浙江大华、阿里巴巴、同花顺这些，目前唯一的短板也就是算法了。开始我准备去letcode、牛客网刷题，但是听说题目挺难的，需要很多时间；反过来想我还不如直接把算法基础和原理弄扎实，到时候随便你题目怎么变化，我都能解决，从原理入手这也是我学习的风格；很庆幸看了真本书，让我彻底搞明白了算法中的那些基础概念：时间复杂度、算法分析方法、算法的价值，还让我看清了“红黑树、快速排序、B树、贪心算法、动态规划、线性规划”这些曾经神秘的存在。在阅读之前，我在豆瓣刷了一下大家的评论，一致认为这本书挺难，是国内众多985/211算法首选教材。我认真看了序言和前言，本书部分内容是针对计算机本科研究生的；而且这是中科大、MIT必修课程；自己能顺利看完整本书，能坚持从序言看到附录，难得。总算也是补上了一个c++程序员最后的技能标签——算法基础。个人觉得，只要把这本书的内容吃透，能够实现书中的所有算法，以后去BAT面试就不用去letcode刷题了。

阅读方法。这本书很厚，电子书一共797页，所以应该稍微快速一点；但是这本书又很难，属于知识密集型书籍，所以也不能太快而错过很多知识点；对于读书的效率问题，建议顺带修炼一下阅读技巧《如何阅读一本书》。我是先从序言开始阅读，了解整本书的结构；全书内容分成七个部分，打了星号的章节是研究生的内容；另外了解到本书是MIT的计算机本科教材，让我对此书肃然起敬。然后我把整个目录抄了一遍，这种做法效果非常好，开始就对整本书有大概的了解，知道本书分成七个部分：基础知识、排序、数据结构、高级设计、高级数据结构、图算法、算法问题选编；结合对序言的阅读，就能知道整本书的结构，有哪些是重点，哪些是难点，有多少刚好是自己想要的知识点。一边读，一遍做笔记太重要了；我使用幕布（http://www.mubu.com）来做阅读笔记，它可以结构化文档，还可以生成思维导图，多终端同步，在好友之间分享，非常推荐；以前我是每读到一个自然段都会停下来思考，并做笔记，这样的吸收率确实挺高，但是速度太慢，有时候进度太慢也让自己感到灰心；现在我是每一个小节做一次笔记，总结重点和个人观点，就按照目录来组织笔记（不知道这样的做法是否合理，探索中） 。阅读完了之后一定要做整体总结，而且要认真做；一遍读完以为自己收货已经很大，其实知识点很杂乱，容易忘，也不方便使用；做个阅读总结，立马会让收获翻倍，散乱的知识能够有序组织起来，还有没搞懂的地方回头来看也能快速搞懂（否则不懂的永远也不会懂了，自己还不知道）。期间跳过了3个小节，有点愧疚，有时候确实读不下去了；有两章基本没看懂，连概念都没理清楚：17章 摊还分析、31章 数论算法，可能是自己的注意力不够集中，脑子里总有些思绪蹦出来，还有有时间压力，以后还要修炼阅读功力。

第一部分 基础知识

1.1 算法基础

这部分非常重要，同时也是全书最简单的章节。阅读这部分能够让我们搞懂那些高大上的算法符号，让我们知道怎么分析算法的好坏，还能见识到几个常见的算法。 作者说算法是一种技术，就像网络编程、图像处理、面向对象等技术一样，这让我很震惊，居然可以这样来看待算法。一个好的算法确实像升级了CPU一样，执行速度更快，能够解决问题；比如归并排序的时间复杂度是O(nlgn), 冒泡排序的时间复杂度是O(n^2)，如果需要排序10^9个数据，冒泡排序需要5.5个小时，归并排序仅需要26分钟，这效果就跟升级了CPU和内存一样；从这个角度上看算法确实就是一个很牛逼的技术，产生的价值很大，因此我们应该重视起来，并潜心修炼。改善程序的运行性能可以从升级硬件、精简代码、实现策略、换个算法角度入手。

1.2 算法的表示

以前我们公司有个刚毕业做算法的同学，对伪代码认识有偏差，可能是没读过这本书；他自己认为伪代码都已经写出来了，你们这些工程师咋还看不懂呢？结果他写的伪代码就是数学公式，还有步骤1/2/3/4，这估计只有自己以为很清晰了，别人都看不懂。作标准的伪代码，应该参照本书的这些表示格式，这在以后工程实践中非常重要，尤其是架构师和做算法的同学，写伪代码应该参考本书的格式。使用英文表达式表示逻辑，借用程序语言中的while/for关键字表示循环， if、else表示分支结构。按照本书的格式写出的伪代码，看起来就像是python代码。如下图：

1.3 算法符号

面试中经常会被问到，某某算法的时间复杂度是多少？我当年都不知道在问啥，亏自己自称高级工程师，其实这些都是算法分析中的基础中的基础问题。算法分析中每条执行指令消耗同等单位资源，而不管是执行的什么语句，比如整数加法、浮点除法、逻辑位运算执行都是消耗单位时间；而且把执行次数的规模作为最终衡量算法的性能指标，而忽略了每次执行指令的条数和额外的常数，比如执行指令总次数为cn+b，每次需要c条指令，预备和结束需要c条指令，然而我们直接说时间复杂度是O(n),而不是O(cn + b)；我们不需要精确求解执行执行次数，而只需要求出一个函数的界，比如冒泡排序算法指令执行次数为是cn^2 + bn + c，但是我们直接说冒泡排序的时间复杂度是O(n^2)，而不是O(cn^2 + bn + c)，感觉就是在偷懒，因为cn^2 + bn + c <= c1n^2(一定能够找到常数c1), 这样表述似乎很严谨，还很简洁，直接记为冒泡排序的时间复杂度是O(n^2)。其实它这样的思想是来源于高中数学中的界函数，T(n)表示精确的指令执行次数，Θ表示紧缺界、（大O）表示上界、（Ω）表示下界、（小写字母o）表示非紧确上界、（ω）表示非紧确下界。如下图：

Θ（n）函数线会一直紧贴着T（n），有可能低于T（n），也可能高于T（n），但一直都是挨着T（n）的；O(n)则会一直高于T（n），而且是挨着的，o(n)一直高于O（n）还高；Ω则一直低于T（n），ω(n)比Ω(n)更低；渐进函数、非紧确渐进函数都是为了简化描述——偷懒。

1.4 算法分析

算法涉及到三个关键点：解决问题、运行时间、运行空间。本书主要分析的是算法运行的时间，数据结构分析的时候会涉及到空间需求的分析；前面说到的那些渐进符号都是表示算法运行时间的函数。分析下面的代码：

INSERTION-SORT(A)         代价     次数
	For j = 2 to A.length      c1        n
		Key = A[j]         c2        n-1
		I = j – 1          c3        n-1
	While I > 0 and A[i] > key c4        ∑ti         (I 2n)
		A[i+1] = A[i]      c5        ∑(ti - 1)     (I 2n) 
		I = I – 1          c6        ∑(ti - 1)     (I 2n)
	A[I + 1] = key             c7         n – 1

精确运行时间：

T(n) = c1.n + c2(n - 1) + c3(n - 1) + c5.∑ti + c6.∑(ti - 1) + c7.∑(ti - 1) + c8(n - 1)

= a.n^2 + b.n + c

渐进运行时间：

紧确界：多项式中，增长率最快的就是最高次数项，因此T(n)的渐进函数一定是k.n^2,再把常数k省略不写，T(n) = Θ(n^2)。

紧确上界：运行时间cn^2 + bn + c <= cεn^2,因此T(n) = O(n^2);

紧缺下界：运行时间一定大于b.n,因此可以说T(n) = Ω(n);

非紧确上界：n^2 <= n^3,可以说T(n)的一个非紧确上界是n^3,即是T(n) = o(n^3)

非紧确下界：n > c （c 小于1）,可以说T(n)的一个非紧确下界是c，即T(n) = ω(c)

回头来看，发现算法分析就是统计出执行代码的总次数，然后使用渐进记号来简洁地描述这个执行时间。自此我们就把伪代码的表示，算法时间复杂度的分析，以及高大上的渐进符号(T(n)/Θ/O/Ω/o/ω)搞清楚了。

1.5 算法设计技术

插入排序使用的是增量方法，在排序子数组A[1..j-1]，然后将A[j]插入适当的位置，把比待插入元素大的元素往后挪一个位置，再把数组元素就从j-1增加到j个，当所有元素都插入新数组的时候整个数组就按照从大到小的顺序排好了。插入排序是不稳定的排序。增量算法的效果并不好，时间复杂度是O(n^2)；还有分治法，它的时间复杂度能达到O(nlgn)，是选择排序中渐进最优的排序;它的核心思想就是将一个大问题 ，递归分解成更小的子问题，然后解决子问题，再把子问题合并起来，就发现大问题已经被解决了；归并排序遵循如下模式：1.分解：分解待排序的n个元素递归为两个n/2个元素的子序列，2.解决，递归排序两个子序列；3.合并，递归合并已经排序的子序列。我们在描述一个算法的时间复杂度的时候常使用的O符号，它其实描述的是最坏情况；有时候我们也可以使用期望（也就是平均时间复杂度）来衡量算法好坏；由此看来算法的时间复杂度是依赖输入序列的特征的。比如在插入排序算法中，当输入序列已经从大到小排好序，运行时间就会发生最坏情况Θ(n^2)，而序列是从小到大，则可以达到最好的运行时间Θ(n)。为去掉对输入序列的依赖，我们可以使用随机策略，将输入序列先用随机算法把顺序打乱，这样就可以得到平均运行时间复杂度。随机算法的效果如下图：

第二部分 排序和顺序统计量

2.1 排序简介

排序算法看起来比较简单，实际上还是需要些技巧，面试中必会问到。大家都知道冒泡排序、插入排序、选择排序这些很简单的算法；如果是稍微高级点的堆排序、快速排序、桶排序就很难在面试临场自己写出来。所以这部分十分重要。在面试中最好不要说冒泡排序，这是c语言入门基础用的排序算法，算法复杂度Ω(n^2)，插入排序是O(n^2)；一说出来就知道你有多low了。

插入排序。代码如下：

效果如图所示：

最坏情况下，每次都要挪动前j个数，挪动总次数就是1+2+3+4+….+A.length -1 = (A.lenth – 1 + 1).A.lenth/2，光看这一个运行逻辑就需要A.lenth^2/2 此，因此运行时间是关于A.length的2次方多项式，时间复杂度就是Θ(n^2).冒泡排序法比插入排序更垃圾，任何情况都要执行Ω(n^2)次比较。

2.2 归并排序

插入排序，选择排序，没学过算法的同学，稍微想想也能做出来，但是归并排序就是体现学过的人与没学过的人的差距了，算法时间复杂度直接降低到O(nlgn),log是以2为底的对数。伪代码如下：

执行效果如下图：

每次将待处理数组分成两半，因此递归层数最多为lgn，lg以2为底；每层要处理的元素规模总数为n，会有n次if，n次复制，n+2次数据初始化，2次递归调用MEGER-SORT，总之每层总执行次数一定是关于n的一次函数cn+b；因此归并排序总的时间复杂度就是O(nlgn)。但是比较坑的是：每次重排都会开辟新的空间，来回两次复制数据；后面会使用原地址排序（快速排序、堆排序），看起来效率更高。

2.3 堆排序

堆排序算法结合了归并排序和插入排序的优点，归并排序时间复杂度是O(nlgn),插入排序可以进行原址排序；克服了归并排序和插入排序的缺点，归并排序处理每个子问题都需要开辟额外的空间，插入排序每次可能遍历向后挪动数据。堆相关的算法都是基于堆数据结构的，而堆数据结构必须满足数组下标号的特殊关系，二叉堆堆是一棵树+一个数组的结合，树的每个节点管理了数组下标号的值。一个堆数据结构必须有三个属性A.length/A.heap-size/A.array。下标号必须满足如下关系：

堆排序的代码如下：

堆排序没有使用额外的存储空间，直接使用原来的数组，操作数组下标完成排序，而且不用真正存储一棵树的结构。完全二插堆的高度是lgn，因此MAX-HEAPIFY(A, i)执行最多lgn次；BUILD-MAX-HEAP(A)最多执行A.length lg(A.length) / 2次；最后排序会遍历执行MAX-HEAPIFY(A) 一共A.length lg A.length，因此排序一共需要执行（3/2）A.length lg A.length，因为A.length == n,所以堆排序的时间复杂度是O(nlgn)。

2.4 快速排序

快速排序期望运行时间平均情况下可以与归并排序相等Θ(nlgn)，而最坏情况与插入排序运行时间相等Θ(n^2)。快速排序使用的是原址排序，而且Θ(nlgn)中隐藏的常数更小，因此在实际中有很好的使用价值。伪代码如下：

算法执行的效果如图：

无限制区域j to r – 1是for循环还没处理的区域；当for循环结束时，将只存在区域pi/ir – 1,然后将r的元素交换到i + 1的位置。

这种分治法的核心就是把数据操作规模变成一棵树，树的每层都是执行Θ(n)次操作，因此性能关键就是树高了；如果数组所有元素都未排序，每次平均划分点就在中间，树的高度就是lgn；如果所有元素都已经排序，每次划分点都在r – 1的位置，导致树高是n，时间复杂度就是Θ(n^2)。为了避免最坏情况的发生，可以使用随机选择主元来打乱排序，期望时间复杂度就可以达到Θ(nlgn)，但输入元素不能都相同。伪代码如下：

RANDOMIZED-QUICKSORT(A, p, r)
	if p < r
		q = RANDOMIZED-PARTITION(A, p ,r)   //计算划分点
		RANDMIZED-QUICKSORT(A, p, q - 1)    //递归处理左边子序列
		RANDMIZED-QUICKSORT(A, q + 1, r)    //递归处理右边子序列

RANDOMIZED-PARTION(A, p, r)
	I = RANDOM(p, r)                  //从p---r中随机选择一个下标号
	exchange A[r] with A[i]           //与最右边的元素交换
	return PARTION(A, p, r)           //计算划分点

2.5 希尔排序

虽然本书没有提到这个排序算法，我看网上一般都会提到；开始我以为类似桶排序，然而事实完全相反；不知道就是不知道，不要觉得好像是就满足了；我去网上查了一下：https://baike.baidu.com/item/希尔排序/3229428?fr=aladdin。原来希尔排序是对插入排序的一种改进，速度比插入排序快，比快排慢；由于它实现简单，性能好，因此一般在项目初期都可以使用这种排序方法。伪代码如下：

SHELL-SORT(A)
	d = n/2                                         //以输入规模一半作为初始步长
	while d > 0                                     //直到d/2 < 0为止
		for i = d to n – 1
			tmp = A[i]
			j = i
			while j >= d and A[j - d] > tmp  //把当前组中比temp大的后移d个位置
				A[j] = A[j - d]
				j = j – d
			A[j] = temp                      //将j放到当前组合适的位置
			d = d/2                          //递归减小步长

执行效果如图：

最多执行lgn趟，每趟执行次数变化规律为：n - n/2,n – n/22 ,n – n/23，时间复杂度是O(nlgn);看起来相对于插入排序的改善就是执行趟数少多了，相对于归并排序内存消耗少多了。希尔排序是不稳定排序。

2.6 线性时间排序

计数排序、计数排序和桶排序都属于线性时间排序，而前面介绍的归并排序、堆排序、选择排序都是基于元素之间的比较，这些比较排序的时间下界为Ω(nlgn)，归并排序和堆排序可以达到渐进最优，而快排可以的达到期望最优，但是基于比较的算法下界是Ω(nlgn)，最多能在系数上有改进。计数排序是通过计算来排序的，可以不受这个下界限制。

2.6.1 计数排序

从“计数排序”的名称上来看，这个算法的秘诀就是计数，它会统计出每个元素前面有多少个比自己小的元素，然后把自己放在那个位置。比如x前面有17个比自己小的元素，那么x就应该放在第18个位置。代码如下：

算法执行效果如下图：

只需要4个for循环，每个循环执行max(k, A.length)，当输入值范围k小于A.length时就时间复杂度就是Θ(n)，就算k值偏大，但总是一个常数，只是多消耗一些内存来计数。重点是计数排序属于稳定排序，这对于作为基数排序的子程序十分重要。稳定排序：具有相同大小的元素在排序前后，输入与输出数组中的相对次序相同，这对于携带卫星数据的输入十分重要。

2.6.2 基数排序

计数排序有个问题，当输入数范围很大的时候，计数数组对内存消耗非常恐怖。比如输入n=10个数，最大值为k=1000 000，为了排序十个数则需要k大小的数组来计数，得不偿失。使用基数排序，就可以把输入数按位拆分，对每个位依次排序，有点分治法的意思，它就自然排序好了。当然这个分治的基础要保证每个子问题排序稳定。代码如下：

排序效果如图：

对每个位排序整个数组，需要进行k次计数，n次赋值，需要Θ(n + k)时间复杂度（k可能比n大，因此k不能忽略）；一共需要d轮排序完成整个排序过程，因此时间复杂度是Θ(d(n + k))。

2.6.3 桶排序

以前听说hash排序，就会想到对输入数据取模运算；听到hash桶还不知道啥意思；尤其是散列碰撞就搞不清楚了；这里对这些概念解释得非常清晰。将输入数组A，取值范围是（c1，c2）；将这个范围平均分成m个区间[Ci, Cj]，每个区间区间就叫一个桶，这也是桶排序名称的来由；多个数可能会被映射到同一个桶（也就是一个区间）中，这就是散列碰撞；将映射到同一个桶中的多个元素用链表连起来，这样就可以解决散列碰撞。对于桶排序来说，待排序的数都映射到桶里面去后，还需要对同一个桶里面的数据进行再排序。伪代码如下：

排序效果：

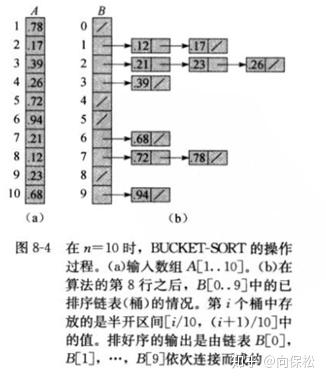
算法执行了三个for循环，每次执行次数是n；因为假设了输入序列均匀，所以对散列碰撞的数进行插入排序时一定是常数时间，因此可以说桶排序的时间复杂度是Θ(n)。值得注意的是计数排序和桶排序都对输入序列做了假设，计数排序需要待排序数范围很小，桶排序需要待排序数值分布均匀，因此这两种排序的应用场景有限。桶映射和解决散列映射的方法很有很多有趣的东西，会在第11章 散列表 深入讲解，值得期待。

面试中经常会被问到哪些排序是稳定的，需要了解一下：

https://www.cnblogs.com/codingmylife/archive/2012/10/21/2732980.html

第三部分 数据结构

编程中的数据结构，算法的数据结构，数学中的集合；作为后面高级算法的基础，前面的排序算法都使用数组搞定了；

对于程序员来说，一说到数据结构，就立马想到变量、结构体、对象、数组、标准容器这些（可能每本介绍语法的编程书籍都是这么说的）；但是算法导论讲的数据结构不是那些，而是栈、队列、链表、散列表、各种树，它与数学中的集合更类似，相当于c++ STL中的容器，那些容器都是基于本章的数据结构；数据结构是后面实现高级算法的基础，比如动态规划、贪心算法、图算法，因此本章十分重要，可能也是那些面试官想要的答案。前面讲的那些排序算法基本都是使用的数组，所以排序算法是非常基础的算法。这些数据结构都支持通用的操作：插入、修改、搜索、删除、获取最大最小值等，有点类似数据库的增删改查，谁叫它们（数据结构）是集合（容器）呢！数据结构的功能主要是来存取数据，而实现各种排序、求最优解等主要靠算法。

3.1 基本数据结构

栈、队列、链表以及对应的操作是高级数据结构的基础，也是程序员的数据结构基础

3.1.1 栈

栈是一个很常用的数据结构，主要是我们的函数嵌套调用就是栈的数据结构；栈的特点是先入后出FILO。但是从数据结构角度看，一定要与函数调用区别开，我曾经见过有程序员只晓得函数栈，这个概念已经被他僵化，再也看不到还有栈数据机构了，实际函数栈只是栈数据结构的一种实现而已。栈必须实现三个操作：STACK-EMPTY(S)/PUSH(S, x)/POP(S)，而且每个操作的时间复杂度是O(1)。最简单地可以使用一个数组来实现一个栈，代码如下:

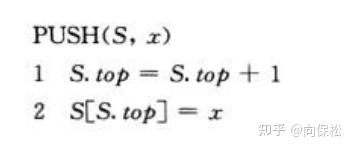
效果如图：

3.1.2 队列

队列与栈刚好对应，取出顺序是先入先出FIFO，也可以使用一个数组来实现。每个操作的时间复杂度都是O(1)。实现代码如下：

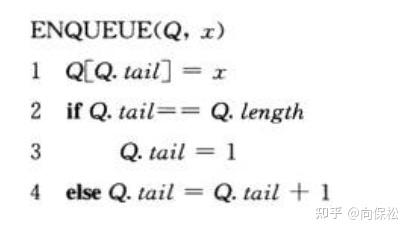
值得注意的是：可能DEQUEUE速度可能比ENQUEUE速度快，这里需要做安全性检测。

3.1.3 链表

链表是我们日常工作中用得最多的数据结构之一，因为他太简单了。从c++的角度来说，链表就是个结构体+两个指针属性的数据结构。链表的特点是增删数据都可以在常数时间内完成，而查询速度最坏需要Θ(n)。链表常用的操作实现如下：

链表的所有操作都是指针，对于没有指针的语言可以使用数组下标号实现prev[i]/key[j]/next[l]。链表看起来十分简单，也没什么特色，但是它是很多高级数据结构的基础，比如二叉树、N叉树、红黑树。链表中有三个关键属性：prev/key/next，而二叉树就是把prev/next修改为left/right，还增加一个指针parent，因此二叉树一共四个属性：parent、key、left、right。二叉树结构图如下：

使用链表扩展到二叉树的思路，K叉树可以增加K个成员，表示K个孩子；但是当孩子节点个数无限的时候，这样既浪费空间又无法满足需求。这些人想处了一种巧妙的方法：左孩子右兄弟的表示方法，就可以表示n叉树，最后节点属性是：left-child/right-sibling/key/parent，N叉树的结构图如下：

以前我一听说堆数据结构就会想到堆内存，然而堆内存是如何维护的，据说是使用的空闲链表；这咋一看怎么跟堆数据结构没有关系了？看到现在我似乎还是不明白堆数据结构是咋样的，但是在第六章用堆实现了一颗完全二叉树；用堆的最末节点+单数组就实现了堆的样子；那么那颗完全二叉树到底是堆，还是树；据说堆应该是可以实现随机存取的；堆数据结构到底长啥样？先把这个疑问留着吧。

3.2 散列表

散列表在关键字查询性能有非常出色的表现，时间复杂度是O(1);它的灵感来源于数组的寻址方式，数组任何元素访问A[i]都可以在O(1)时间内完成；但是当关键字范围远大于元素数目时，数组寻址方法就非常浪费空间，还有如果关键字是字符串就更不好处理；于是这些天才就想出了散列表这么个数据结构，他们将任何关键字（实数、字符串）映射成有限的自然数集{0, 1, 2, 3…N}；这样的操作既节约空间，又可以有接近数组查询的性能。散列还有一个问题，那就是散列碰撞；多个不同的关键字可能映射成同一个关键字；可以通过链表或者开放寻址的方法解决散列碰撞。使用双链表解决散列碰撞后，散列的常用操作伪代码如下：

数据结构图示如下：

在hash表中最关键的两个问题分别是：散列冲突和hash函数。散列冲突可以使用双链表、开放寻址、完全散列（又称多级散列）来解决，非常简单；hash函数是个很有学问的问题。常用的hash算法有除法hash和乘法hash。设计散列函数的核心就是让关键字尽量均匀分布到各个桶里面去。

除法hash：h(k) = k mod m。这里有个关键技巧就是对m的选择，尽量为一个素数，且这个素数不接近2^p。

乘法hash：1. 用关键字乘上一个常数A(0 < A < 1)，提取kA的小数部分；2.用m乘以这个值并向下取整。函数为：h(k) = m(kA mod 1)。

全域散列hash：除法散列和乘法散列虽然简单，但是最坏情况可能的导致所有元素都映射到一个桶中，全域散列可以解决这个问题。全域散列中全域的意思是函数簇是全域的。函数如下：hab(k) = ( (ak + b) mod p ) mod m,这里p是一个素数，m是映射关键字最大值，a、b是p域中的任何值，这样hab就是一个函数簇即全域的。素数a、b、p是编译器选择的，m会根据输入数量调整。对于a、b、p的关系需要结合31章 数论算法 来证明。

3.3 二叉搜索树

这种树对二叉树做了一些限制，x.key > x.left.key 且x < x.right.key。二叉搜索树支持的有SEARCH、MINIMUM、PREDECESSOR、SUCCESSOR、INSERT、DELETE等。二叉搜索树结构如下图：

各种操作的代码如下：

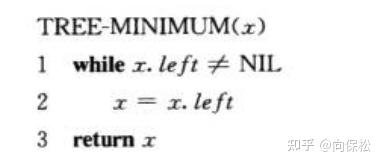
删除操作太复杂必须上个图：

二叉搜索树所有操作时间复杂度都依赖于树的高度h，输入数据随机均匀分布的情况下树的高度是lg(n)，这时候时间复杂度是O(lgn)。最坏情况树的高度可能是n，这时候各种操作都跟链表没区别。可以使用红黑树保证树高为lg(n)。

3.4 红黑树

红黑树是完全平衡搜索树（基于二叉搜索树）中的一种，它也是链表的一种变体，相对于二叉搜索树增加了一个属性color，这个属性可以设置为red或者black，因此红黑树一共有5个属性：color/key/left/right/p。红黑树必须满足5个要求，这是保证树高不会超过2lg(n + 1)近似平衡的根本原因，要求如下：

1. 每个节点要么是红色，要么是黑色；
2. 根节点是黑色；
3. 每个叶节点(NIL)是黑色；
4. 如果一个节点是红色，则它的两个子节点都是黑色；
5. 对每个节点，从该节点到所有后代的叶节点的简单路径上，均包含相同数目的黑色节点；

红黑树首先满足二叉搜索树的基本性质x.k > x.left.k and x.k < x.right.key，而且树高为O(lg)，因此红黑树上的各种操作SEARCH、PREDECESSOR、SUCCESSOR、MINIMUM、MAXIMUM、INSERT、DELETE的时间复杂度均为O(lgn)。但是对于INSERT、DELETE操作修改了红黑树中元素的指针，因此破坏了红黑树的基本性质，这需要一些操作恢复红黑树的性质。伪代码如下：

情况太复杂上图：

插入操作首先将节点添加到底部，并着色为红色；这有可能违反了红黑性质（父节点为红色，两个子节点必须为黑色）；从z开始沿树向上重新着色和旋转以恢复红黑性质。一共分为三种情况，在RB-COLOR-FIXUP中已经标出；情况1：如果父亲和叔叔都是红色，直接将其都染色成黑色(bh + 1)，这样就增加了这两条路径的黑高，为了保证每条路径的黑高相等，必须将祖父节点染色成红色(bh - 1)；应为爷爷变成红色，所以必须迭代检测爷爷节点的红黑性质；情况2：只有父亲节点是红色，而且自己还是个右子节点，那就把父节点左旋一下（这里为什么要这么做）；这样操作之后明显有连续两个节点是红色的；情况3：只有父节点是红色，而且自己是个左节点，直接把父亲染色成黑色，再把爷爷染成红色，这可能导致叔祖父黑高减少，因此必须右旋一下。整个操作过程都是向上操作，因此操作次数最多lgn，因此RB-INSERT(T, x)时间复杂度是O(lgn)。

RB-DELETE（T, z）

y = z

y original-color = y.color

if z.left == T.nil

x = z.right

RB-TRANSOLANT(T, z, z.right)

elseif z.right == T.nil

x = z.left

RB-TRANSLANT(T, z, z.left)

else

y = TREE-MINIMUM(z.right)

y-oringinal-color = y.color

x = y.right

if y.p == z

x.p = y

else

RB-TRANSPLANT(T, y, y.right)

y.right = z.right

y.righy.p = y

RB-TRANSPLANT(T, z, y)

y.left = z.left

y.left.p = y

y.color = z.color

if y-original-color == BLACK

RB-DELETE-FIXUP(T, x)

RB-TRNSLANT(T, u, v)

if u.p == T.nil

T.root = v

elseif u == u.p.left

u.p.left = v

else

u.p.right = v

v.p = u.p

RB-DELETE-FIXUP(T, x)

while x != T.root and x.color == BLACK

if x == x.p.left

w = x.p.right

if w.color == RED

w.color = BLACK //case 1

x.p.color = RED //case 1

LEFT-ROTATE(T, x.p) //case 1

w = x.p.right //case 1

if w.left.color == BLACK and w.right.color == BLACK

w.color = RED //case 2

x = x.p //case 2

else if w.right.color == BLACK

w.left.color == BLACK //case 3

w.color = RED //case 3

RIGHT-ROTATE(T, w) //case 3

w = x.p.right //case 3

else

w.color = x.p.color //case 4

x.p.color = BLACK //case 4

w.right.color = BLACK //case 4

LEFT-ROTATE(T, x.p) //case 4

x = T.root //case 4

else

w.color = x.p.color

x.p.color = BLACK

w.right.color = BLACK

LEFT-ROTATE(T, x.p)

x = T.root

x.color = BLACK

删除重新着色过程比插入过程还复杂，必须上图：

着色过程太复杂，暂时不做分析了，但愿面试中不要碰到。

3.7 散列表

第四部分 高级设计和分析技术

前面学习的都是基础知识。分析算法的时间复杂度是用的所有执行指令条数之和，这样只能对单个算法问题进行分析；但是有些问题需要多次不同操作杂糅在一起，比如vector的空间扩展和搜索，当空间足够的时候这些操作的时间复杂度都是O(1)，但是空间不够的时候需要重新申请一大块内存，而且还要把原始数据全部拷贝过去，看起来非常耗时，这场算法问题你无法用指令相加的方式来分析时间复杂度，只能把指令相加作为一个基础，这些复杂的算法分析可以使用本章的聚合分析、核算法、势能法进行分析。去年哈曼中国的时候被问到c++ vector的内存增长和减少方式，我居然一脸懵逼；如果能够用本书的知识给他们分析一遍，绝对会让面试官眼前一亮。前面居然用了一个部分4章来讲排序算法，然而它们都是针对一个特定的问题，只有第4章和第5章提出的分治策略、随机算法可以推广到其它问题上；这章使用了动态规划和贪心算法来求解所有最优问题，而且时间复杂度都是多项式时间，当然它们其实继承了分治策略的思想。

4.1 高级分析技术

摊还分析。书中的介绍顺序是先介绍动态规划和贪心算法，我觉得应该先介绍摊还分析，就像书的最开始是介绍了时间复杂度的分析一样，而且动态规划中海用了本章提到的聚合分析。因此我觉得还是从这个知识点学起比较好，另外本章并没有涉及到任何动态规划和贪心算法的知识。

前面的算法时间复杂度分析都是使用的最坏情况，但是这个最坏情况不是太精确；使用聚合分析可以得到更加紧缺的界。比如二进制递增计数问题，一个k位的二进制数，二进制的每个位用数组A来存放，代码如下：

INCREMENT(A)
	i = 0
	While i < A.length and A[i] == 1
		A[i] = 0
		i = i + 1
	if i < A.length
		A[i] = 1

从最坏的角度来分析，每次执行INCREMENT最多需要k= A.length次循环；执行n次INCREMENT调用一共需T(n) = O(kn)次调用，摊还代价就是T(n)/n = O(k)；而实际上每个位反转次数是有规律的，A[1]反转n/2,A[2]反转n/4,A[3]翻转n/8....A[n]翻转n/2^k，n次操作每个位一共翻转次数∑n/2^i = 2n = T(n)，摊还代价就是T(n)/n = O(1)；如果多次操作这个INCREMENT这个函数，实际代价是常数时间，远比使用最坏方法分析的O(k)小。由此可见聚合分析厉害了我的哥。最坏分析只看一次操作，聚合分析看平均代价，更有全局视角，更符合日常使用。

核分析。聚合分析给每个操作赋予相同的摊还代价，而核分析给不同的操作赋予不同的摊还代价。每个操作都有固定的实际代价(指令执行数量)a1，摊还代价p1可以用来支付实际代价，因此每次执行对应的操作之后剩余信用为p1 – a1；执行其它操作的时候，这个对象的信用就是p2 + p1 – a1 – a2；只要保证剩余信用大于0即可，不管你给每个操作多少摊还代价。以栈操作为例：

实际代价：PUSH = 1, POP = 1, MULTIPOP = min(k, s)

摊还代价：PUSH = 2, POP = 0, MULTIPOP = 0

执行n次PUSH后，栈中存储的摊还代价之和为2n = O(n)，n次POP和MULTIPOP摊还代价为：2n + 0n + 0n，因此n个PUSH、POP、MULTIPOP序列的操作总摊还代价就是2n。感觉这种方法科学性不够，分析难度很大，不知道怎么去给每个操作赋予多少摊还代价。

势能分析。它跟数据结构建立了一个映射关系，数据结构为Di，势能就为φ(Di)；而且这个值跟操作次数有关，比如栈PUSH n次，栈里面就存了n个对象，势能就变成n；势能分析很抽象，并没有像核分析那样说每个PUSH增加1个势能，一个POP降低一个势能那么直观。也就是说我们把视角从指令执行次数上移开，而关注指令执行的结果，n次PUSH操作就是存了n个对象，n个POP，或者n个MULTIPOP就是让存储数据量变为0了，总的来看它们就是一个生产者消费者模式，这样我们只看有效操作，不管这些操作怎么组合，只看结果还剩多少对象，我们就估计出总的摊还代价。每次操作之后的摊还代价等于实际代价+势能积累：Ci’ = Ci +φ(Di) -φ(Di-1)，总摊还代价为∑Ci’ = ∑Ci +φ(Di) - φ(D0)；因为φ(Di) - φ(D0) >= 0,所以∑Ci’ >= ∑Ci, 摊还代价∑Ci’就是实际代价的一个上界。我是概念懂了。

总的来说，摊还分析比最坏分析结果更加精确，而且可以分析多个组合操作的平均代价，只是分析方法更加复杂，需要观察规律，依赖操作结构。最坏情况分析适合的场景是对输入结果不确定，比如排序算法中不同输入可能导致不同的时间复杂度。

4.2 动态规划

我对动态规划、矩阵运算、线性规划、单纯形算法容易混淆；动态规划是求解单选型问题最优解；矩阵运算是求解一组方程的解；线性规划是根据一组不等式，求最大最小值问题；单纯形算法是求解线性规划问题的一种牛逼方法。哪些问题适合动态规划？答案是：最优子结构 + 子结构重叠。如果一个问题的最优解包含子问题的最优解，我们称这个问题具有最优子结构；子问题的空间应该足够小，即递归算法会反复求解相同的子问题，而不是一直产生新的子问题。应用动态规划需要4个步骤：

1.刻画一个最优解的结构特征；

2.递归地定义最优解的值；

3.求解最优解的值，通常采用自底向上的方法；

4.利用计算出的信息构造一个最优解；

应用动态规划解决钢条切割问题，问题描述如下：

（非动态规划）自顶向下递归调用的伪代码如下：

CUT-ROAD(p, n)
	if n == 0
		return 0
	q = -∞
	for i = 1 to n
		q = max(q, p[i] + CUT-ROAD(p, n - i))
	return q;

切割方案又2^(n - 1)，当n = 40时，需要运行几分钟才能求解；使用动态规划求解伪代码如下：

MEMOIZED-CUT-ROD(p ,n)                  //自顶向下递归切割
	let r[0..n] be a new array      //创建一个备忘录数组
	for i = 0 to n
		r[i] = -∞
	return MEMOIZED-CUT-ROD-AUX(p, n, r)

MEMOIZED-CUT-ROD-AUX(p, n, r)
	if r[n] >= 0                            //已经存在备忘录价格，直接返回
		return r[n]
	if n == 0
		q = 0
	else
		q = -∞
		for i = 1 to n                   //尝试所有子问题最优价格
			q = max(q, p[i] + MEMOIZED-CUT-ROD-AUX(p, n – i, r))
		r[n] = q                       //对计算结果做个备忘
	return q

BOTTOM-UP-CUT-ROD(p, n)                        //自底向上的备忘录
	let r[0..n]be a new array
	r[0] = 0
	for j = 1 to n
		q = -∞
		for i = 1 to j
			q = max(q, p[i] + r[j - i])
		r[j] = q
	return r[n]

BOTTOM-UP-CUT-ROD有两个for循环，时间复杂度为O(n^2)，相对于递归求解的时间复杂度O(2^(n - 1))改善很大。

4.3 贪心算法

任何贪心算法的问题都可以用动态规划求解，但是反过来不成立；他们都需要问题具有最优子结构特点。贪心算法求解更快，设计更加简单，因此能用贪心算法的地方尽量不用动态规划。动态规划的最优解依赖子问题的最优解，而贪心算法不依赖子问题的最优解，而是包含子问题的最优解；因此动态规划都是自底向上的求解，而且需要备忘录；贪心算法是自顶向上地求解，不需要备忘录。贪心算法设计步骤如下：

1. 确定问题的最优子结构；
2. 设计一个递归算法；
3. 证明我们如果做出了一个最优选择，则只剩下一个子问题；
4. 证明贪心选择总是安全的；
5. 将递归算法转为迭代算法；

使用贪心算法求解活动调度问题：

ACTIVITY-SELECTOR(s, f, 0, n)
	RECURSIVE-ACTVITY-SELECTOR(s, f, k, n)	      //递归选择最早开始活动
                m = k + 1                             //当前活动下标
		while m <= n and s[m] < f[k]          //选择出可以被调用的下一个活动
			m = m + 1
		if m <= n                  	      //还有活动可以调度
			return {Am}U RECURSIVE-ACTIVITY-SELECTOR(s, f, m, n)  //递归选最早开始活动
		else return ∅

这些活动必须先按照最早开始时间排序，然后使用贪心算法就可以得到最多活动调度数量。发现这个贪心算法中并没有使用备忘录，使用聚合分析，每个活动最多被选择一次，因此时间复杂度是O(n)。大名鼎鼎的赫夫曼编码居然是基于贪心算法的，赫夫曼编码在图像或者文本压缩领域地位非常重要，压缩比可以达到20%~90%。算法伪代码如下：

HUFFMAN(C)
	n = |C|                               //取得元素数量n
	Q = C                                 //开始把所有元素放到最小二叉树里面
	for i = 1 to n – 1                    //将每个元素都放到完全二叉树
		allocate a new node z
		z.left = x = EXTRACT-MIN(Q)   //取一个最小值作为左节点
		z.right = y = EXTACT-MIN(Q)   //再取一个最小值作为右节点
		z.freq = x.freq = y.freq      //新节点的频率为左右节点的和
		INSERT(Q, z)                  //将新节点放回去
	return EXTRACT-MIN(Q)                 //返回根节点

执行图示如下：

整个过程一个for循环，需要执行n – 1次，堆操作时间复杂度是O(lgn)，因此HUFFMAN编码为O(nlgn)。贪心算法问题其实是一个拟阵问题，有向无环图是一个拟阵，因此所有贪心问题可以转化为一个带权重的有向无环图求解最优解问题。

第五部分 高级数据结构

如果说第三部分 数据结构 是程序员的一次飞跃，从此揭开红黑树、散列表、二叉搜索树的面纱，知道了c++ vector、map、heap这些容器的实现原理；那么这个部分就是一次基因突变，看到计算机科学的冰山一角，算法可以这么快，快到突破比较排序的Ω(nlgn)和线性排序的Ω(n),从此认为数据库引擎的核心数据结构B树是那么简单。

5.1 B树

它是二叉树的一个变种，只不过它每个节点不是2个子节点，而是t个；它是众多平衡搜索树中的一种，专门针对磁盘IO而设计。在需要磁盘IO的场景中，算法的时间复杂度处理考虑指令执行次数，磁盘IO也对运行时间产生了重要影响；辅助设备相对于CPU和主存来说速度慢100 000倍。磁盘的结构如下：

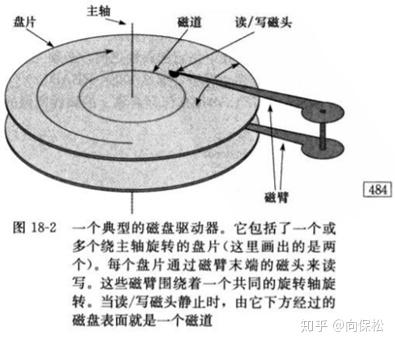
综上所述，磁盘读写的速度主要取决于读取次数；因此涉及到磁盘IO的算法，需要最小化读写次数；B树将每个节点的大小存储在一个磁盘页上，大小是2^11~2^14 byte，因此一个节点大概能存1000个关键字；B+树又是B树的一个变种，节点只存储关键字和指向卫星数据的指针，卫星数据保存在叶节点上。B树每个节点能存储t = 50~2000个关键字，而且是一颗完全平衡树，因此树高为O(lgn)，lg底数t很大，因此树高很小，在查找的时候只需要很少的磁盘读写，而且每个节点都在一个磁盘页上，在磁盘上的存储结构如下图：

一颗B树T是具有以下性质的有根树：

1. 每个节点x有如下属性：
1. x.n,当前存储在节点x的关键字个数
2. x.n个关键字x.key[i]本身x.key1, x.key2...x.keyn,以非降序存放，使得x.key1 <= x.key2 <= … <= x.keyn；
3. x.leaf,一个布尔值，如果x是叶节点，则为TRUE；如果x为内部节点，则为FALSE；

1. 每个内部节点x有x.n + 1个指向孩子的指针x.c[n + 1],叶节点没有孩子，所以它们的x.c[i]没有意义；
2. 关键字x.key[i]对各个子树的关键字范围加以分割，如果ki为存储在任意一个x.c[i]为根的子树中的关键字集合，那么k1 <= x.key1 <= key2 <= x.key2 <= … <= x.keyn <= kn+1;
3. 每个叶节点具有相同深度，即树的高度h；
4. 每个节点所包含的关键字个数有上界和下界。用一个被称为B树的最小度数的固定整数t >= 2来表示这些界；
1. 除了根节点以外的每个节点必须至少有t – 1个关键字。因此除了根节点以外的每个内部节点至少有t个孩子。如果树非空，根节点至少有一个关键字。
2. 每个节点最多包含2t – 1个关键字。因此一个内部节点至多有2t个孩子。当一个节点有2t – 1个孩子时，称该节点是满的。

B树支持的操作如下：

B-TREE-SEARCH(x, k)
	i = 1
	while i <= x.n and k > x.keyi      //找到关键字可能所在区间
		i = i + 1
	if i < x.n and k == x.keyi         //本节点找到关键字则返回节点和所在位置
		return (x, i)
	elseif x.leaf                      //叶节点都还没找到，说明没有该关键字
		return NIL
	else
		DISK-READ(x, ci)           //先从磁盘中读取该对应子节点到内存
		return B-TREE-SEARCH(x.ci, k)

B-TREE-CREATE(T)
	x = ALLOCATE-NOD()
	x.leaf = TRUE
	x.n = 0
	DISK-WRITE(x)                 //保存新节点到磁盘
	T.root = x

B-TREE-SPLIT-CHILD(x, i)
	z = ALLOCATE-NODE()            //分配一个新节点

	y = x.ci                       //取出当前节点的指针
	z.leaf = y.leaf                //继承节点属性
	z.n = t – 1                    //新节点的个数初始化为t - 1

	for j = 1 to t – 1             //把指向节点的关键字都拷贝到新节点上去，第一个不拷贝
		z.keyj = y.keyj + 1   
    
	if not y.leaf                  //如果不是叶节点，还要把对应关键字的节点指针给拷贝到新节点
		for j = i to t
			z.cj = y.cj+t
	y.n = t – 1                    //分裂节点的关键字数减半       
	for j = x.n downto i           //将i之后的指针依次后挪一个位置，类似插入排序
		x.cj+1 = x.cj
	x.ci+1 = z                     //新节点作为y的父节点的一个关键字，放到i + 1处

	for j = x.n downto i           //将关键字依次后挪一个位置
		x.keyj+1 = x.keyj
	x.keyi = y.keyi                //将待分裂处的关键字放到挪出来的那个父节点位置

	x.n = x.n + 1                  //父节点关键字+1

	DISK-WRITE(y)                  //更新分裂节点
	DISK-WRITE(z)                  //写入新节点
	DISK-WRITE(x)                  //更新父节点

操作过程如下图：

B-TREE-INSERT(T, k)
	r = T.root 
	if r.n == 2t – 1              //发现根节点已经满，预先分裂一波，只有这里增加树高
		s = ALLOCATE-NODE()
		T.root = s
		s.leaf = FALSE
		s.n = 0
		s.c1 = r              //每个s.c1都指向父节点？
		B-TREE-SPLIT-CHILD(s, 1)
		B-TREE-INSERT-NONFULL(s, k)
	else
		B-TREE-INSERT-NONFULL(r, k)

B-TREE-INSERT-NONFULL(x.ci, k)
	i = x.n
	if x.leaf                           //是叶节点就插入到合适位置, 只有叶节点接受插入
		while i >= 1 and k < x.keyi
			x.keyi+1 = x.keyi
			i = i – 1
		x.keyi+1 = k
		x.n = x.n + 1
		DISK-WRITE(x)                //更新节点
	else 
                while i >= and k < x.keyi    //找到对应的指针
			i = i – 1
		i = i + 1
		DISK-READ(x.ci)               //读取对应的节点
		if x.ci.n == 2t – 1           //发现节点已经满了就分裂
			B-TREE-SPLIT-CHILD(x, i)
			if k > x.keyi
				i = i + 1
		B-TREE-INSERT-NONFULL(x.ci, k)  //递归插入

整个操作过程如下图：

5.2 斐波那契堆

斐波那契数是我们熟悉的概念，但是斐波那契堆名称的由来仅仅是因为斐波那契堆节点数的一个下界是斐波那契数。斐波那契堆为什么在高级数据结构中呢？因为它有几个操作都能在常数时间内完成，在图算法中有很核心的地位，性能对比如下图：

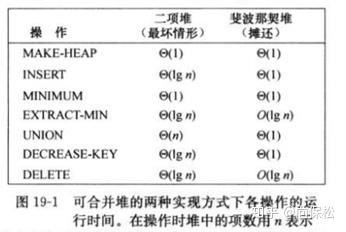
一个斐波那契堆是一系列具有最小堆序的有根树集合。每棵树均遵循最小堆性质：每个节点的关键字大于等于它父节点的关键字。如下图：

斐波那契堆尽可能地将一些可合并堆的操作延后，这就是这些操作时间复是O(1)的秘密；只有EXTRACT-MIN操作，移除堆的最小节点后，才会重新平衡整个堆。各种操作伪代码如下：

FIN-HEAP-INSERT(H, x)
	x.degree = 0
	x.p = NIL
	x.child = NIL
	x.min = FALSE
	if H.min = NIL                           //第一个节点，根指向这个节点
		create a root list for H containing just x
		H.min = x
	else
		insert x into H’s root list              //直接放在根链上
		if x.key < H.min.key                  //如果比最小值小，则更新最小值
			H.min = x
	H.n = H.n + 1                            //堆数量 +1

FIB-HEAP-UNION(H1, H2)
	H = MAKE-FIB-HEAP()
	H.min = H1.min
	concatenate the root list of H2 with the root list of H
	if (H1.min == NIL) or (H2.min != NIL and H2.min.key < H1.min.key)
		H.min = H2.min
	H.n = H1.n + H2.n
	return H

FIB-HEAP-EXTRACT-MIN(H)   //删除最小节点
	z = H.min
	if z != NIL
		for each child x of z
			add x to the root list of H
			x.p = NIL
	remove z from the root list of H
	if z == z.right
		H.min = NIL
	else
		H.min = z.right
CONSOLIDATE(H)
	H.n = H.n – 1
return z

CONSOLIDATE(H)
	let A[0..D(H.n)] be a new array
	for I = 0 to D(H.n)
		A[i] = NIL
	for each node w in the root list of H
		x = w
		d = x.degree
		while A[d] != NIL               //如果这个度数有堆了，就把新的链拼接上来
			y = A[d]
			if x.key > y.key             //更新合成堆的最小值
				exchange x with y
			FIB-HEAP-LINK(H, y, x)      //连接两个最小堆
			A[d] = NIL                //连接后，堆的度+1，原堆删除
			d = d + 1
		A[d] = x                      //把堆放到对应的度位置
	H.min = NIL
	for I = 0 to D(H.n)
		if A[i] != NIL
			if H.min == NIL             //第一次重新创建一个根链，第一个元素是A[i]
				create a root list for H containing just A[i]
				H.min = A[i]         //最小节点为A[i]
			else
				insert A[i] into H’s root list     //插入根链
					if A[i].key < H.min.key     //根据情况更新最小节点
						H.min < A[i]

FIB-HEAP-LINK(H, y, x)
	remove y from the root list of H            //从根链删除y
	make y a child of x, incrementing x.degree   //将y添加为x的一个子节点，度+1
	y.mark = FALSE

经过操作之后，又重新获得了最小值；而且根链的个数不会超过最大度数，因为根链上新的节点都是从度数组拿出来的，而且每个堆的度都不相同；整个操作过程时间复杂度是O(lgn)。

操作过程如下图：

FIB-HEAP-DECREASE-KEY(H, x, k)
	if K < x.key
		error “new key is greater than current key”
	x.key = k
	y = x.p
	if y != NIL and x.key < y.key
		CUT(H, x, y)
		CASCADING-CUT(H, y)
	if x.key < H.min.key
	H.min < x

CUT(H, x, y)
	remove x from the child list of y, decrementing y.degree  //把x从y剪切到根链上，y 度-1
	and x to the root list of H             //度数是剪切一次-1，链接一次+1，与树高无关
	x.p = NIL
	x.mark = FALSE

CASCADING-CUT(H, y)
	z = y.p
	if z != NIL
		if y.mark == FALSE              //第一次失去孩子标记一下
			y.mark = TRUE
		else                         //第二次失去孩子，直接剪切到根连上去
			CUT(H, y, z)
			CASCADING-CUT(H, z)       //递归剪切

FIB-HEAP-DELETE(H, x)
	FIB-HEAP-DECRESE-KEY(H, x, -∞)
	FIB-HEAP-EXTRACT-MIN(H)

删除操作直接复用减值和删除最小值，避免代码冗余，优秀！

5.3 van Emde Boas树

这是目前动态集合操作最快的数据结构，时间复杂度可以达到lglgu

。可以用在优先队列上，比二叉堆、红黑树、斐波那契堆都要好。唯一的缺点就是数据结构稍微有点复杂，包好的属性有T.vEB(size)/T.u/T.min/T.max/T.summary[size1/2]/T.cluster[size1/2]。另外这个数据只能位来表示，每个数组里面的值只能位0/1，不能是十进制值；而且是一个递归数据结构，sizei = sizei-1(1/2)。van Emde Boas树结构的灵感来源于数组+二叉树，数组的随机存取时间复杂度是O(1),然而MAX、MINIMUM、SUCCESSOR这些的时间复杂度是O(n),然后那些天才灵机一动就把位数组与二叉树做了一个叠加，效果如下：

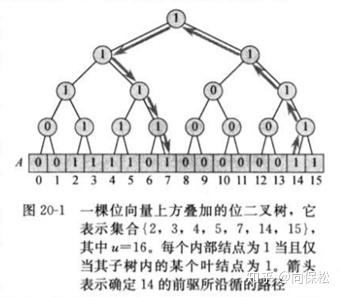
这种方法仅仅比红黑树好一点，MEMBER操作时间复杂度是O(1)，而红黑树需要O（lgn）。为什么红黑树操作慢了，因为树高太高为lgn，于是可以通过叠加一个恒定高度的树进一步降低时间复杂度，如下图：

改进后的对于MAX、MINIMUM、SUCCESSOR、DELETE的操作都变成O(u1/2)，似乎时间复杂度反而没有红黑树优秀了，然而还是比数组好不少。但是这是van Emde Boas原型树的灵感来源。我们把summary数组里面的值单独拿出来又作为元素值的高位x/u1/2，增加一个cluster数组数组存储指向x%u1/2,还使用一个属性存u，修改后的结构如下图：

这个数据结构基本达到目标，动态集合的各种时间复杂度达到O(lglgu)。伪代码如下：

PROTO-vEB-MEMBER(V, x)  //判断值x是否存在
	if V.u == 2
		return V.A[x]     //1 存在， 0 不存在
	else
		return PROTO-vEB-MEMBER(V.cluster[high(x), low(x)])

PROTO-vEB-MINIMUM(V)  //查找最小值
	if V.u == 2
		if V.A[0] = = 1    //第一个有值就是0
			return 0
		elseif V.A[1] == 1    //第二个有值就是1
			return 1
		else
			return NIL   //两个位0元素不存在
	else
		min-cluster = PROTO-vEB-MINIMUM(V.summary)  //获取x/u1/2最小
		if min-cluster == NIL
			return NIL
		else
			offset = PROTO-vEB-MINIMUM(V.cluster[min-cluster])  //获得x%u1/2的最小值
			return index(min-cluster, offset)        //min-cluster*u1/2 + offset

PROTO-vEB-SUCCESSOR(V, x)  //获得后继元素值
	if V.u == 2             
		if x == 0 and V.A[1] == 1  //看该元素的后面有没元素，有则返回1
			return 1
		else                  //该节点后面没有有效值了就返回NIL
			return NIL
	else
		offset = PROTO-vEB-SUCCESSOR(V.cluster[high(x)], low(x))  //
		if offset != NIL						
			return index(high(x), offset)     //这样计算出来的结构实际就比x大1
		else
			succ-cluster = PROTO-vEB-SUCCESSOR(V.summary, high(x)) //找x/u1/2中的后一个
			if succ-cluster == NIL
				return NIL
			else
				offset = PROTO-vEB-MINIMU(V.cluster[succ-cluster])//获得x%u1/2的最小值
				return index(succ-cluster, offset)

PROTO-vEB-INSERT(V, x)
	if V.u == 2
		V.A[x] = 1
	else
		PROTO-vEB-INSERT(V.susmary, high(x))

从上面的代码中，发现proto-vEB结构有很多缺陷，大多数操作都需要多次递归。为了克服最后的缺陷，van Emde Boas树终于诞生了。就一个改进：将max和min直接作为每个proto-vEB的属性。这样MAXMUM、MINIMUM操作就不用递归了，可以在O(1)时间内完成；SUCCESOR可以避免一个判断值x的后继是否在高位的递归调用。数据结构如下图：

各种动态集合操作的伪代码操作如下：

high(x) = x/u1/2

low(x) = x mod u1/2

index(x, y) = x u1/2 + y

vEB-TREE-MINIMUM(V)
	return V.min

vEB-TREE-MAXIMUM(V)
	return V.max

vEB-TREE-MEMBER(V, x)
	if x == V.min or x == V.man
		return TRUE
	elseif V.u == 2
		return FALSE
	else
		return vEB-TREE-MEMBER(V.cluster[high(x)], low(x))

vEB-TREE-SUCCESOR(V, x)
	if V.u == 2
		if x == 0 and V.man == 1  //
			return 1
		else
			return NIL
	elseif V.min != NIL and x < V.min
		return V.min
	else
		max-low = vEB-TREE-MAXIMUM(V.cluster[high(x)])
		if max-low != NIL and low(x) < max-low  //后继在同一个簇中的后面一个
			offset = EB-TREE-SUCCESSOR(V.cluster[high(x)], low(x))
			return index(high(x), offset)
		else
			succ-cluster = vEB-TREE-SUCCESSOR(V.summary, high(x)) //查 x/u1/2中下一个值
			if succ-cluster == NIL
				return NIL
			else
				offset = vEB-TREE-MINIMUM(V.cluster[succ-cluster])//查x/u1/2簇中最小值
				return index(succ-cluster, offset)

vEB-TREE-PREDECESSOR(V, x)
	if V.u == 2
		if x == 1 and V.min == 0  //在同一个簇中有值
			return 0
		else
			return NIL
	elseif V.max != NIL and x > V.max //比max还大，那就是max了
		return V.max
	else
		min-low = vEB-TREE-MINIMUM(V.cluster[high(x)])
		if min-low != NIL and low(x) > min-low   //在同一个簇中
			offset = vEB-TREE-PREDECESSOR(V.cluster[high(x)], low(x))
			return index(high(x), offset)
		else
			pred-cluster = vEB-TREE-PREDECESSOR(V.sumary, high(x))
			return index(pred-cluster, offset)

vEB-EMPTY-TREE-INSERT(V, x)
	V.min = x
	V.max = x

vEB-TREE-INSERT(V, x)
	if V.min == NIL
		vEB-EMPTY-INSERT(V, x)
	elseif x < V.min
		exchange x with V.min
	if V.u > 2
		if eRB-TREE-MINIMUM(V.cluster[high(x)]) == NIL
			vEB-TREE-INSERT(V.summary, high(x))
			vEB-EMPTY-TREE-INSERT(V.cluster[high(x)], low(x))
		else
			vEB-TREE-INERT(V.cluster[high(x)], low(x))
		if x > V.max
			V.max = x

vEB-TREE-DELETE(V, x)
	if V.min == V.max
		V.min = NIL
		V.min = NIL
	elseif V.u == 2
		if x == 0
			V.min = 1
		else
			V.min = 0
			V.max = V.min
	elseif x == V.min
		first-cluster = vEB-TREE-MINIMUM(V.summary)
		x = index(first-cluster, vEB-TREE-MINIMUM(V.cluster[first-cluster]))
		V.min = x
		vEB-TREE-DELETE(V.cluster[high(x)], low(x))
		if vEB-TREE-MINIMUM(V.cluster[high(x)]) == NIL
			vEB-TREE-DELETE(V.susmary, high(x))
			if x == V.max
				summary = vEB-TREE-MAXIMU(V.summary)
				if susmary-max == NIL
					V.max = V.min
				else
				 V.max=index(summary-max,vEB-TREE-MAXIMUM(V.cluster[summary-max]) 
			elseif x == V.max
				V.max = index(high(x)), vEB-TREE-MAXIMUM(V.cluster[high(x)])

van Emde Boas树的核心思想就是就是把x/n1/2, x%n1/2递归处理，这个数据结构是递归格式，导致算法也是递归格式。从数组+二叉树的思想可以看出：把这些基础数据结构灵活地结合可以创造出更好的数据结构或者算法。我自己也还不是很懂，先把原理图和伪代码记录下来，以备需要的时候复习。

总结

后面还有两个部分的知识未做总结，是关于图算法和算法选编的；其中算法选编中的多线程算法和数论算法非常有价值；在面试或者平时工程中多线程用得很多，能够从算法的角度进行思考就比码农高一个思维层次；还有数论是加密解密、数字签名的理论基础，公钥私钥的概念在工程中也用得非常多；但是由于时间关系，这些不能全部总结了；等有空再好好研究一下，算留有一个小小的缺憾。

不过熟练掌握前面五个部分的内容，算是进入了算法的世界，从此拥有了算法的基因，看到计算机科学的一角——动手前先证明可行性。算法选编主要涉及到计算机科学研究方面的东西，理论性非常强，也很抽象。

这段时间我读了《深入linux内核架构》，这本书1000页，像本字典；开始看也很难，不过只要仔细跟着作者思路走，再配合源代码，平时工作中也挺高过相关概念，整体读下来虽然有些卡壳，但是基本都能理解到，讲得出来。我还读了《系统架构》，这本书是非常抽象的文科书籍，最后还涉及到人工智能的一些思想，不过只要认真做笔记，都能全部理解。只有这本书，我认真做了笔记，还有30%没看懂；有很多概念都是全新的，有很多证明就是在做数学推理；不过总算花半个月时间看完，一周总结完，连做梦自己的学习成绩都变好了（哈哈哈，这可能是智商在成长的表现）——值。我越来越坚信：有效地刻意练习，能力就会从骨子里慢慢增长，直到有一天来无影去无踪。