进化策略及其在深度学习中的应用

中国科学院大学计算机软件与理论博士

进化策略及其在深度学习中的应用

本文翻译自：https://lilianweng.github.io/lil-log/2019/09/05/evolution-strategies.html,这篇博文很早就看过，但是每次都是似懂非懂，各种数学公式，虽然我做这个方向的研究很久，但是仍然不能全懂。这个端午，闲来无事，便萌生了翻译的念头，在此分享给各位对这个方向感兴趣的同学们。进化计算近年来的应用领域也一直被拓展，在很多领域展现了很好的性能，是个不错的研究方向。当研究到Fisher信息矩阵时竟发现与几何流形竟也有一定的相关性。深知知识的相通性，学海无涯，希望能再接再厉，对这一领域探知一二。

在学习最优模型参数时，梯度下降不是唯一的选择。在我们不知道目标函数的精确解析形式或不能直接计算梯度的情况下，进化策略(ES)是有效的。这篇文章深入探讨了几个经典的ES方法，以及如何在深度强化学习中使用ES。

随机梯度下降是优化深度学习模型的普遍选择。然而，这并不是唯一的选择。在黑盒优化算法中,可以评估目标函数f(x):ℝn→ℝ,即使你不知道目标函数精确的解析形式,因此无需计算梯度或海赛矩阵。黑箱优化方法的实例有模拟退火法、爬坡法和 Nelder-Mead method等一系列算法。

进化策略(ES)是一种黑箱优化算法，诞生于进化算法(EA)家族。这篇文章将深入介绍一些经典的ES方法，并介绍ES如何在深度强化学习中发挥作用的一些应用。

什么是进化策略

进化策略(ES)属于进化算法的大家庭。ES的优化目标是实数的向量,x∈ℝn。

进化算法是一种基于种群划分的优化算法，其灵感来自自然选择。自然选择认为，具有有利于生存的特性的个体可以世代生存，并将好的特性传给下一代。进化是在选择过程中逐渐发生的，进化使种群生长得能更好地适应环境。

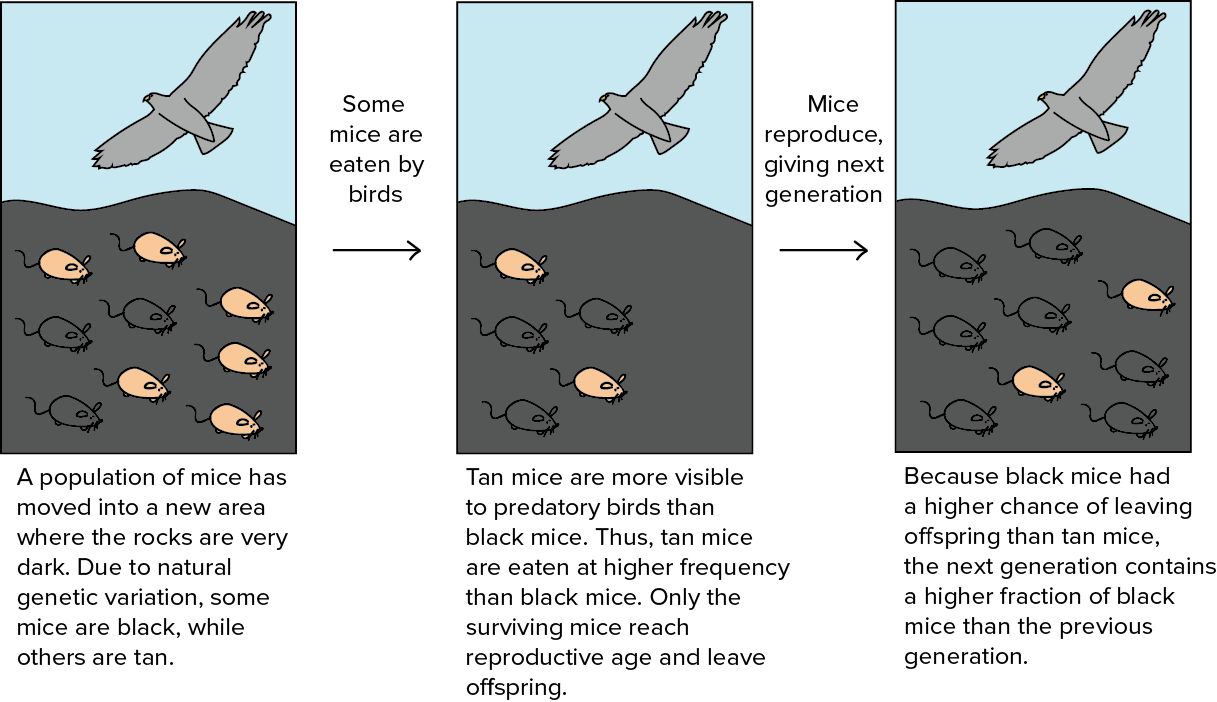
进化算法作为一种通用的优化方案，可以归纳为以下格式:

假设我们想优化一个函数f(x)但f(x)的梯度难以求解。只能得到在特定x下f(x)的确定值。

我们认为随机变量 x 的概率分布 p_θ(x) 是函数 f (x) 优化问题的一个较优的解，θ 是分布 p_θ(x) 的参数。j我们最终的目标是找到 θ 的最优设置。

在给定固定分布形式（例如，高斯分布）的情况下，参数 θ 包含了最优解的知识，在一代与一代间进行迭代更新。

初始化参数θ，我们可以连续地更新θ通过以下三步循环：

产生初始采样种群 D=\left\{\left(x_{i}, f\left(x_{i}\right)\right\}\right.，x_{i} \sim p_{\theta}(x).
评估采样种群的”适应度“值。
选择最优子集来更新参数θ，最优子集的选择通常是根据适应度值或者是排序。

简单高斯进化策略

简单高斯进化策略是进化策略的最基础和最经典的版本。它将p_{\theta}(x) 建模为一个n维的各向同性的高斯分布，在高斯分布中 θ 指的是均值 \mu 和标准差\sigma

\theta=(\mu, \sigma), p_{\theta}(x) \sim \mathcal{N}\left(\mu, \sigma^{2} I \sim \mu+\sigma \mathcal{N}(0, I)\right. \\

简单高斯进化策略的流程如下，给定x \in \mathcal{R}^{n} ：

初始化参数 \theta = \theta_{0},计数器 t = 0
从高斯分布中采样种群大小为\Lambda的后代种群：

D^{(t+1)}=\left\{x_{i}^{(t+1)} \mid x_{i}^{(t+1)}=\mu^{(t)}+\sigma^{(t)} y_{i}^{(t+1)} \text { where } y_{i}^{(t+1)} \sim \mathcal{N}(x \mid 0, \mathbf{I}), i=1, \ldots, \Lambda\right\} \\

选择出使得 f (x_i) 最优的 λ 个样本组成的子集，该子集被称为「精英集」。为了不失一般性，我们可以考虑 D(t+1) 中适应度排名靠前的 k 个样本，将它们放入「精英集」。我们可以将其标注为：

D_{\text {elite }}^{(t+1)}=\left\{x_{i}^{(t+1)} \mid x_{i}^{(t+1)} \in D^{(t+1)}, i=1, \ldots, \lambda, \lambda \leq \Lambda\right\} \\

接着，我们使用「精英集」为下一代种群估计新的均值和标准差：

\mu^{(t+1)}=\operatorname{avg}\left(D_{\mathrm{elite}}^{(t+1)}\right)=\frac{1}{\lambda} \sum_{i=1}^{\lambda} x_{i}^{(t+1)} \\\sigma^{(t+1)^{2}}=\operatorname{var}\left(D_{\mathrm{elite}}^{(t+1)}\right)=\frac{1}{\lambda} \sum_{i=1}^{\lambda}\left(x_{i}^{(t+1)}-\mu^{(t)}\right)^{2} \\

重复（2）-（4）步直到结果足够好。

协方差自适应进化策略

标准差 σ 决定了探索的程度：当 σ 越大时，我们就可以在更大的搜索空间中对后代种群进行采样。在简单高斯演化策略中，σ(t+1) 与 σ(t) 密切相关，因此算法不能在需要时（即置信度改变时）迅速调整探索空间。

「协方差矩阵自适应演化策略」（CMA-ES）通过使用协方差矩阵 C 跟踪分布上得到的样本两两之间的依赖关系，解决了这一问题。新的分布参数变为了：

\theta=(\mu, \sigma, C), p_{\theta}(x) \sim \mathcal{N}\left(\mu, \sigma^{2} C\right) \sim \mu+\sigma \mathcal{N}(0, C) \\

其中，σ 控制分布的整体尺度，我们通常称之为「步长」。

在我们深入研究 CMA-ES 中的参数更新方法前，不妨先回顾一下多元高斯分布中协方差矩阵的工作原理。作为一个对称阵，协方差矩阵 C 有下列良好的性质：

C 始终是对角阵
C 始终是半正定矩阵
所有的特征值都是非负实数
所有特征值都是正交的
C 的特征向量可以组成 Rn 的一个标准正交基

令矩阵 C 有一个特征向量 B=\left[b_{1}, \dots, b_{n}\right] 组成的标准正交基，相应的特征值分别为 \lambda_{1}^{2}, \ldots, \lambda_{n}^{2}。令 D=diag (λ1,…,λn).

C=B^{\top} D^{2} B=\left[\begin{array}{cccc}\mid & \mid & & \mid \\ b_{1} & b_{2} & \dots & b_{n} \\ \mid & \mid & & \mid\end{array}\right]\left[\begin{array}{cccc}\lambda_{1}^{2} & 0 & \dots & 0 \\ 0 & \lambda_{2}^{2} & \dots & 0 \\ \vdots & \dots & \ddots & \vdots \\ 0 & \dots & 0 & \lambda_{n}^{2}\end{array}\right]\left[\begin{array}{ccc}- & b_{1} & - \\ - & b_{2} & - \\ & \dots & \\ - & b_{n} & -\end{array}\right] \\

C 的平方根为：

C^{\frac{1}{2}}=B^{\top} D B \\

更新均值

\mu^{(t+1)}=\mu^{(t)}+\alpha_{\mu} \frac{1}{\lambda} \sum_{i=1}^{\lambda}\left(x_{i}^{(t+1)}-\mu^{(t)}\right) \\

CMA-ES 使用 α_{μ}≤1 的学习率控制均值 μ 更新的速度。通常情况下，该学习率被设置为1，从而使上述等式与简单高斯演化策略中的均值更新方法相同.

控制步长

采样过程可以与均值和标准差的更新解耦：

x_{i}^{(t+1)}=\mu^{(t)}+\sigma^{(t)} y_{i}^{(t+1)}, \text { where } y_{i}^{(t+1)}=\frac{x_{i}^{(t+1)}-\mu^{(t)}}{\sigma^{(t)}} \sim \mathcal{N}(0, C) \\

参数 σ 控制着分布的整体尺度。它是从协方差矩阵中分离出来的，所以我们可以比改变完整的协方差更快地改变步长。步长较大会导致参数更新较快。为了评估当前的步长是否合适，CMA-ES 通过将连续的移动步长序列相加\frac{1}{\lambda} \sum_{i}^{\lambda} y_{i}^{(j)}, j=1, \ldots,t构建了一个演化路径（evolution path）p_σ。通过比较该路径与随机选择（意味着每一步之间是不相关的）状态下期望会生成的路径长度，我们可以相应地调整 σ（详见下图）。

每次演化路径都会以同代中的平均移动步长 y_i 进行更新。

\begin{array}{l}\frac{1}{\lambda} \sum_{i=1}^{\lambda} y_{i}^{(t+1)}=\frac{1}{\lambda} \frac{\sum_{i=1}^{\lambda} x_{i}^{(t+1)}-\lambda \mu^{(t)}}{\sigma^{(t)}}=\frac{\mu^{(t+1)}-\mu^{(t)}}{\sigma^{(t)}} \\ \frac{1}{\lambda} \sum_{i=1}^{\lambda} y_{i}^{(t+1)} \sim \frac{1}{\lambda} \mathcal{N}\left(0, \lambda C^{(t)}\right) \sim \frac{1}{\sqrt{\lambda}} C^{(t)^{\frac{1}{2}}} \mathcal{N}(0, I) \\ \text { Thus } \sqrt{\lambda} C^{(t)^{-\frac{1}{2}} \frac{\mu^{(t+1)}-\mu^{(t)}}{\sigma^{(t)}}} \sim \mathcal{N}(0, I)\end{array} \\

通过与 C^{-1/2} 相乘，我们将演化路径转化为与其方向相独立的形式。

C^{(t)-\frac{1}{2}}=B^{(t)^{\top}} D^{(t)^{-\frac{1}{2}}} B^{(t)} 的工作原理如下：

B(t) 包含 C 的特征向量的行向量。它将原始空间投影到了正交的主轴上。
D^{(t)^{-\frac{1}{2}}}=\operatorname{diag}\left(\frac{1}{\lambda_{1}}, \ldots, \frac{1}{\lambda_{n}}\right) 将各主轴的长度放缩到相等的状态。
{B^{(t)}}^T 将空间转换回原始坐标系.

为了给最近几代的种群赋予更高的权重，我们使用了「Polyak 平均」算法（平均优化算法在参数空间访问轨迹中的几个点），以学习率 α_σ 更新演化路径。同时，我们平衡了权重，从而使 p_σ 在更新前和更新后都为服从 N (0,I) 的共轭分布（更新前后的先验分布和后验分布类型相同）。

\begin{aligned} p_{\sigma}^{(t+1)} &=\left(1-\alpha_{\sigma}\right) p_{\sigma}^{(t)}+\sqrt{1-\left(1-\alpha_{\sigma}\right)^{2}} \sqrt{\lambda} C^{(t)^{-\frac{1}{2}} \frac{\mu^{(t+1)}-\mu^{(t)}}{\sigma^{(t)}}} \\ &=\left(1-\alpha_{\sigma}\right) p_{\sigma}^{(t)}+\sqrt{c_{\sigma}\left(2-\alpha_{\sigma}\right) \lambda} C^{(t)^{-\frac{1}{2}}} \frac{\mu^{(t+1)}-\mu^{(t)}}{\sigma^{(t)}} \end{aligned} \\

随机选择得到的 p_σ 的期望长度为 E‖N (0,I)‖，该值是服从 N (0,I) 的随机变量的 L2 范数的数学期望。按照图 2 中的思路，我们将根据 ‖pσ(t+1)‖/E‖N (0,I)‖ 的比值调整步长：

\begin{aligned} \ln \sigma^{(t+1)} &=\ln \sigma^{(t)}+\frac{\alpha_{\sigma}}{d_{\sigma}}\left(\frac{\left\|p_{\sigma}^{(t+1)}\right\|}{\mathbb{E}\|\mathcal{N}(0, I)\|}-1\right) \\ \sigma^{(t+1)} &=\sigma^{(t)} \exp \left(\frac{\alpha_{\sigma}}{d_{\sigma}}\left(\frac{\left\|p_{\sigma}^{(t+1)}\right\|}{\mathbb{E}\|\mathcal{N}(0, I)\|}-1\right)\right) \end{aligned} \\

其中，dσ≈1 是一个衰减参数，用于放缩 lnσ 被改变的速度。

自适应协方差矩阵

我们可以使用精英样本的 yi 从头开始估计协方差矩阵（y_i∼N(0,C)）

C_{\lambda}^{(t+1)}=\frac{1}{\lambda} \sum_{i=1}^{\lambda} y_{i}^{(t+1)} y_{i}^{(t+1)^{\top}}=\frac{1}{\lambda \sigma^{(t)^{2}}} \sum_{i=1}^{\lambda}\left(x_{i}^{(t+1)}-\mu^{(t)}\right)\left(x_{i}^{(t+1)}-\mu^{(t)}\right)^{\top} \\

只有当我们选择出的种群足够大，上述估计才可靠。然而，在每一代中，我们确实希望使用较小的样本种群进行快速的迭代。这就是 CMA-ES 发明了一种更加可靠，但同时也更加复杂的方式去更新 C 的原因。它包含两种独立的演化路径：

秩 min (λ, n) 更新：使用 {C_λ} 中的历史，在每一代中都是从头开始估计的。
秩 1 更新：根据历史估计移动步长 y_i 以及符号信息

第一条路径根据 {C_λ} 的全部历史考虑 C 的估计。例如，如果我们拥有很多代种群的经验，C^{(t+1)} \approx \operatorname{avg}\left(C_{\lambda}^{(i)} ; i=1, \ldots, t\right) 就是一种很好的估计方式。类似于 p_σ，我们也可以使用「polyak」平均，并且通过学习率引入历史信息：

C^{(t+1)}=\left(1-\alpha_{c \lambda}\right) C^{(t)}+\alpha_{c \lambda} C_{\lambda}^{(t+1)}=\left(1-\alpha_{c \lambda}\right) C^{(t)}+\alpha_{c \lambda} \frac{1}{\lambda} \sum_{i=1}^{\lambda} y_{i}^{(t+1)} y_{i}^{(t+1)^{\top}} \\

通常我们选择的学习率为：\alpha_{c \lambda} \approx \min \left(1, \lambda / n^{2}\right).

第二条路径试图解决 y_{i} y_{i}^{\top}=\left(-y_{i}\right)\left(-y_{i}\right)^{\top} 丢失符号信息的问题。与我们调整步长 σ 的方法相类似，我们使用了一个演化路径 p_c 来记录符号信息，p_c 仍然是种群更新前后都服从于 N (0,C) 的共轭分布。

我们可以认为 p_c 是另一种计算 avg_i(y_i) 的（请注意它们都服从于 N (0,C)），此时我们使用了完整的历史信息，并且能够保留符号信息。请注意，在上一节中，我们已经知道了\sqrt{k} \frac{\mu^{(++1)}-\mu^{(t)}}{\sigma^{()}} \sim \mathcal{N}(0, C).

p_c 的计算方法如下：

\begin{aligned} p_{c}^{(t+1)} &=\left(1-\alpha_{c p}\right) p_{c}^{(t)}+\sqrt{1-\left(1-\alpha_{c p}\right)^{2}} \sqrt{\lambda} \frac{\mu^{(t+1)}-\mu^{(t)}}{\sigma^{(t)}} \\ &=\left(1-\alpha_{c p}\right) p_{c}^{(t)}+\sqrt{\alpha_{c p}\left(2-\alpha_{c p}\right) \lambda} \frac{\mu^{(t+1)}-\mu^{(t)}}{\sigma^{(t)}} \end{aligned} \\

接下来，通过p_c来更新协方差矩阵：

C^{(t+1)}=\left(1-\alpha_{c 1}\right) C^{(t)}+\alpha_{c 1} p_{c}^{(t+1)} p_{c}^{(t+1)^{\top}} \\

当 k 较小时，秩 1 更新方法相较于秩 min (λ, n) 更新有很大的性能提升。这是因为我们在这里利用了移动步长的符号信息和连续步骤之间的相关性，而且这些信息可以随着种群的更新被一代一代传递下去。

最后，我们将两种方法结合起来：

C^{(t+1)}=\left(1-\alpha_{c \lambda}-\alpha_{c 1}\right) C^{(t)}+\alpha_{c 1} \underbrace{p_{c}^{(t+1)} p_{c}^{(t+1)^{\top}}}_{\text {rank-one update }}+\alpha_{c \lambda} \underbrace{\frac{1}{\lambda} \sum_{i=1}^{\lambda} y_{i}^{(t+1)} y_{i}^{(t+1)^{\top}}}_{\text {rank-min(lambda, n) update }} \\

在上面所有的例子中，我们认为每个优秀的样本对于权重的贡献是相等的，都为 1/λ。该过程可以很容易地被扩展至根据具体表现为抽样得到的样本赋予不同权重 w_1,…,w_λ 的情况。

The CMA Evolution Strategy: A Tutorial

自然演化策略

自然演化策略（Wierstra 等人于 2008 年发表的 NES）在参数的搜索分布上进行优化，并将分布朝着自然梯度所指向的高适应度方向移动。

自然梯度

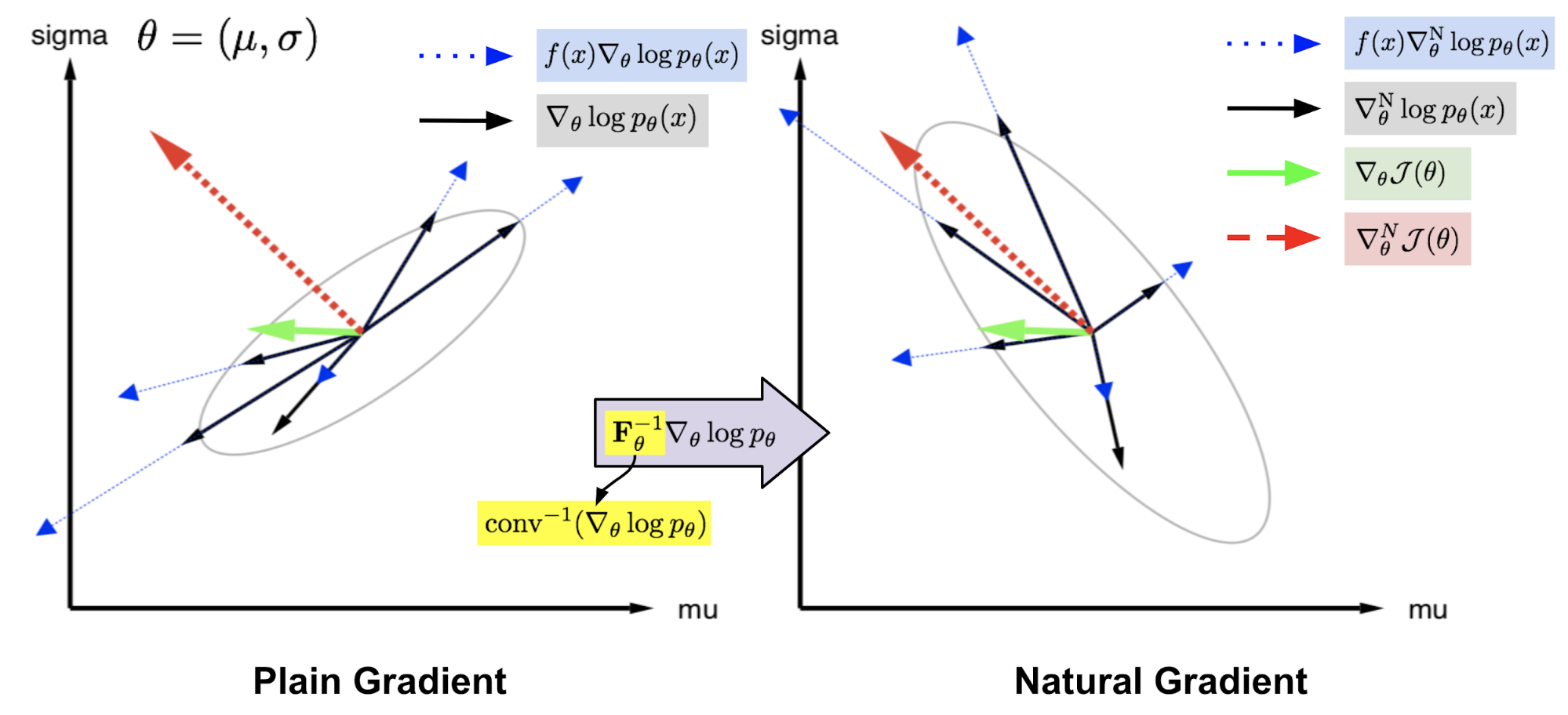
给定一个参数为 θ 的目标函数 J (θ)，我们的目标是找到最优的 θ，从而最大化目标函数的值。朴素梯度会以当前的 θ 为起点，在很小的一段欧氏距离内找到最「陡峭」的方向，同时我们会对参数空间施加一些距离的限制。换而言之，我们在 θ 的绝对值发生微小变化的情况下计算出朴素梯度。优化步骤如下：

d^{*}=\underset{\|d\|=\epsilon}{\operatorname{argmax}} \mathcal{J}(\theta+d), \text { where } \epsilon \rightarrow 0 \\

不同的是，自然梯度用到了参数为 θ, p_θ(x)（在 NES 的原始论文中被称为「搜索分布」）的概率分布空间。它在分布空间中的一小步内寻找最「陡峭」（变化最快）的方向，其中距离由 KL 散度来度量。在这种限制条件下，我们保证了每一步更新都是沿着分布的流形以恒定的速率移动，不会因为其曲率而减速。

d_{\mathrm{N}}^{*}=\underset{\mathrm{KL}\left[p_{\theta} \| p_{\theta+d}\right]=\epsilon}{\operatorname{argmax}} \mathcal{J}(\theta+d) \\

使用 Fisher 信息矩阵进行估计

但是如何精确地计算\mathrm{KL}\left[p_{\theta} \| p_{\theta+\Delta \theta}\right]? 通过推导log P_{\theta + d} 在 \theta 处的Taylor展开得到：

\begin{array}{l}\mathrm{KL}\left[p_{\theta} \| p_{\theta+d}\right] \\ =\mathbb{E}_{x \sim p_{\theta}}\left[\log p_{\theta}(x)-\log p_{\theta+d}(x)\right] \\ \approx \mathbb{E}_{x \sim p_{\theta}}\left[\log p_{\theta}(x)-\left(\log p_{\theta}(x)+\nabla_{\theta} \log p_{\theta}(x) d+\frac{1}{2} d^{\top} \nabla_{\theta}^{2} \log p_{\theta}(x) d\right)\right] \quad ; \text { Taylor expand } \log p_{\theta+d} \\ \approx-\mathbb{E}_{x}\left[\nabla_{\theta} \log p_{\theta}(x)\right] d-\frac{1}{2} d^{\top} \mathbb{E}_{x}\left[\nabla_{\theta}^{2} \log p_{\theta}(x)\right] d\end{array} \\

其中：

\begin{aligned} \mathbb{E}_{x}\left[\nabla_{\theta} \log p_{\theta}\right] d &=\int_{x \sim p_{\theta}} p_{\theta}(x) \nabla_{\theta} \log p_{\theta}(x) \\ &=\int_{x \sim p_{\theta}} p_{\theta}(x) \frac{1}{p_{\theta}(x)} \nabla_{\theta} p_{\theta}(x) \\ &=\nabla_{\theta}\left(\int_{x} p_{\theta}(x)\right) \\ &=\nabla_{\theta}(1)=0 \end{aligned} \\

最终，我们得到：

\mathrm{KL}\left[p_{\theta} \| p_{\theta+d}\right]=-\frac{1}{2} d^{\top} \mathbf{F}_{\theta} d, \text { where } \mathbf{F}_{\theta}=\mathbb{E}_{x}\left[\left(\nabla_{\theta} \log p_{\theta}\right)\left(\nabla_{\theta} \log p_{\theta}\right)^{\top}\right] \\

其中，Fθ 被称为 Fisher 信息矩阵。由于 E[∇θlogpθ]=0，所以 Fθ 也是 ∇θlogpθ 的协方差矩阵：

针对以下的优化问题：

\max \mathcal{J}(\theta+d) \approx \max \left(\mathcal{J}(\theta)+\nabla_{\theta} \mathcal{J}(\theta)^{\top} d\right) \quad \text { s.t. } \mathrm{KL}\left[p_{\theta} \| p_{\theta+d}\right]-\epsilon=0 \\

我们可以通过拉格朗日乘子法找到上述问题的解：

\begin{aligned} \mathcal{L}(\theta, d, \beta) &=\mathcal{J}(\theta)+\nabla_{\theta} \mathcal{J}(\theta)^{\top} d-\beta\left(\frac{1}{2} d^{\top} \mathbf{F}_{\theta} d+\epsilon\right)=0 \text { s.t. } \beta>0 \\ \nabla_{d} \mathcal{L}(\theta, d, \beta) &=\nabla_{\theta} \mathcal{J}(\theta)-\beta \mathbf{F}_{\theta} d=0 \\ \text { Thus } d_{\mathrm{N}}^{*} &=\nabla_{\theta}^{\mathrm{N}} \mathcal{J}(\theta)=\mathbf{F}_{\theta}^{-1} \nabla_{\theta} \mathcal{J}(\theta) \end{aligned} \\

其中 {d_N}^∗仅仅提取了忽略标量 β^{−1} 的情况下，在 θ 上最优移动步长的方向。

NES算法

我们将与一个样本相关联的适应度标记为 f (x)，关于 x 的搜索分布的参数为 θ。我们希望 NES 能够优化参数 θ，从而得到最大的期望适应度：

\mathcal{J}(\theta)=\mathbb{E}_{x \sim p_{\theta}(x)}[f(x)]=\int_{x} f(x) p_{\theta}(x) d x \\

在这里，我们使用与蒙特卡洛策略梯度强化中相同的似然计算技巧：

\begin{aligned} \nabla_{\theta} \mathcal{J}(\theta) &=\nabla_{\theta} \int_{x} f(x) p_{\theta}(x) d x \\ &=\int_{x} f(x) \frac{p_{\theta}(x)}{p_{\theta}(x)} \nabla_{\theta} p_{\theta}(x) d x \\ &=\int_{x} f(x) p_{\theta}(x) \nabla_{\theta} \log p_{\theta}(x) d x \\ &=\mathbb{E}_{x \sim p_{\theta}}\left[f(x) \nabla_{\theta} \log p_{\theta}(x)\right] \end{aligned} \\

除了自然梯度，NES 还采用了一些重要的启发式方法让算法的性能更加鲁棒。

NES 应用了基于排序的适应度塑造（Rank-Based Fitness Shaping）算法，即使用适应度值单调递增的排序结果，而不是直接使用 f (x)。它也可以是对「效用函数」进行排序的函数，我们将其视为 NES 的一个自由参数。
NES 采用了适应性采样（Adaptation Sampling）在运行时调整超参数。当进行 θ→θ′ 的变换时，使用曼 - 惠特尼 U 检验（[Mann-Whitney U-test]）对比从分布 p_θ 上采样得到的样本以及从分布 p_{θ′} 上采样得到的样本。如果出现正或负符号，则目标超参数将减少或增加一个乘法常数。请注意，样本 x′_{i}∼p_{θ′}(x) 的得分使用了重要性采样权重 w′_i=p_θ(x)/p_θ′(x)。

应用：深度强化学习中的演化策略

OpenAi用于强化学习的演化策略

将演化算法应用于强化学习的想法可以追溯到很久以前的论文「Evolutionary Algorithms for Reinforcement Learning」（论文地址：https://arxiv.org/abs/1106.0221），但是由于计算上的限制，这种尝试仅仅止步于「表格式」强化学习（例如，Q-learning）。

受到 NES 的启发，OpenAI 的研究人员（详见 Salimans 等人于 2017 年发表的论文「Evolution Strategies as a Scalable Alternative to Reinforcement Learning」，论文链接：https://arxiv.org/abs/1703.03864）提出使用 NES 作为一种非梯度黑盒优化器，从而寻找能够最大化返回函数 F (θ) 的最优策略参数 θ。

这里的关键是，为模型参数 θ 加入高斯噪声 ε，并使用似然技巧将其写作高斯概率密度函数的梯度。最终，只剩下噪声项作为衡量性能的加权标量。

假设当前的参数值为 \hat{\theta}（区别于随机变量 θ）。我们将 θ 的搜索分布设计为一个各向同性的多元高斯分布，其均值为 \hat{\theta}，协方差矩阵为 σ^2I

\theta \sim \mathcal{N}\left(\hat{\theta}, \sigma^{2} I\right) \text { equivalent to } \theta=\hat{\theta}+\sigma \epsilon, \epsilon \sim \mathcal{N}(0, I) \\

θ 更新的梯度为：

\begin{array}{l}\nabla_{\theta} \mathbb{E}_{\theta \sim \mathcal{N}\left(\hat{\theta}, \sigma^{2} I\right)} F(\theta) \\ =\nabla_{\theta} \mathbb{E}_{\epsilon \sim \mathcal{N}(0, I)} F(\hat{\theta}+\sigma \epsilon) \\ =\nabla_{\theta} \int_{\epsilon} p(\epsilon) F(\hat{\theta}+\sigma \epsilon) d \epsilon \\ =\int_{\epsilon} p(\epsilon) \nabla_{\epsilon} \log p(\epsilon) \nabla_{\theta} \epsilon F(\hat{\theta}+\sigma \epsilon) d \epsilon \\ =\mathbb{E}_{\epsilon \sim \mathcal{N}(0, I)}\left[\nabla_{\epsilon}\left(-\frac{1}{2} \epsilon^{\top} \epsilon\right) \nabla_{\theta}\left(\frac{\theta-\hat{\theta}}{\sigma}\right) F(\hat{\theta}+\sigma \epsilon)\right] \\ =\mathbb{E}_{\epsilon \sim \mathcal{N}(0, I)}\left[(-\epsilon)\left(\frac{1}{\sigma}\right) F(\hat{\theta}+\sigma \epsilon)\right] \\ =\frac{1}{\sigma} \mathbb{E}_{\epsilon \sim \mathcal{N}(0, I)}[\epsilon F(\hat{\theta}+\sigma \epsilon)]\end{array} \quad \text { , Gaussian } p(\epsilon)=(2 \pi)^{-\frac{n}{2}} \exp \left(-\frac{1}{2} \epsilon^{\top} \epsilon\right) \\

其中 \int_{\epsilon} p(\epsilon) \nabla_{\epsilon} \log p(\epsilon) \nabla_{\theta} \epsilon F(\hat{\theta}+\sigma \epsilon) d \epsilon 是所用到的似然计算技巧。

在每一代中，我们可以采样得到许多 εi，i=1,…,n，然后并行地估计其适应度。一种优雅的设计方式是，无需共享大型模型参数。只需要在各个工作线程之间传递随机种子，就足以事主线程节点进行参数更新。随后，这种方法又被拓展成了以自适应的方试学习损失函数。

Evolution Strategies as a Scalable Alternative to Reinforcement Learning

为了使算法的性能更加鲁棒，OpenAI ES 采用了虚拟批量归一化（Virtual BN，用于计算固定统计量的 mini-batch 上的批量归一化方法），镜面采样（Mirror Sampling，采样一对 (−ϵ,ϵ) 用于估计），以及适应度塑造（Fitness Shaping）技巧。

使用演化策略进行探索

在强化学习领域，「探索与利用」是一个很重要的课题。上述演化策略中的优化方向仅仅是从累积返回函数 F (θ) 中提取到的。在不进行显式探索的情况下，智能体可能会陷入局部最优点。

新颖性搜索（Novelty-Search）演化策略（NS-ES，详见 Conti 等人于 2018 年发表的论文「Improving Exploration in Evolution Strategies for Deep Reinforcement Learning via a Population of Novelty-Seeking Agents」）通过朝着最大化「新颖性得分」的方向更新参数来促进探索。

「新颖性得分」取决于一个针对于特定领域的行为特征函数 b (π_θ)。对 b (π_θ) 的选择取决于特定的任务，并且似乎具有一定的随机性。例如，在论文里提到的人形机器人移动任务中，b (π_θ) 是智能体最终的位置 (x,y)。

将每个策略的 b (π_θ) 加入一个存档集合 \mathcal{A}。
通过 b (π_θ) 和 \mathcal{A} 中所有其它实体之间的 K 最近邻得分衡量策略 π_θ 的新颖性。（文档集合的用例与「情节记忆」很相似）

N(\theta, \mathcal{A})=\frac{1}{\lambda} \sum_{i=1}^{\lambda}\left\|b\left(\pi_{\theta}\right), b_{i}^{\mathrm{knn}}\right\|_{2}, \text { where } b_{i}^{\mathrm{knn}} \in \mathrm{kNN}\left(b\left(\pi_{\theta}\right), \mathcal{A}\right) \\

在这里，演化策略优化步骤依赖于新颖性得分而不是适应度：

\nabla_{\theta} \mathbb{E}_{\theta \sim \mathcal{N}\left(\hat{\theta}, \sigma^{2} I\right)} N(\theta, \mathcal{A})=\frac{1}{\sigma} \mathbb{E}_{\epsilon \sim \mathcal{N}(0, I)}[\epsilon N(\hat{\theta}+\sigma \epsilon, \mathcal{A})] \\

NS-ES 维护了一个由 M 个独立训练的智能体组成的集合（「元 - 种群」），\mathcal{M}={θ_1,…,θ_M}。然后选择其中的一个智能体，将其按照与新颖性得分成正比的程度演化。最终，我们选择出最佳策略。这个过程相当于集成，在 SVPG 中也可以看到相同的思想。

\begin{aligned} m & \leftarrow \operatorname{pick} i=1, \ldots, M \text { according to probability } \frac{N\left(\theta_{i}, \mathcal{A}\right)}{\sum_{j=1}^{M} N\left(\theta_{j}, \mathcal{A}\right)} \\ \theta_{m}^{(t+1)} & \leftarrow \theta_{m}^{(t)}+\alpha \frac{1}{\sigma} \sum_{i=1}^{N} \epsilon_{i} N\left(\theta_{m}^{(t)}+\epsilon_{i}, \mathcal{A}\right) \text { where } \epsilon_{i} \sim \mathcal{N}(0, I) \end{aligned} \\

其中，N 是高斯扰动噪声向量的数量，α 是学习率。

NS-ES 完全舍弃了奖励函数，仅仅针对新颖性进行优化，从而避免陷入极具迷惑性的局部最优点。为了将适应度重新考虑到公式中，研究人员又提出了两种变体。

NSR-ES

\theta_{m}^{(t+1)} \leftarrow \theta_{m}^{(t)}+\alpha \frac{1}{\sigma} \sum_{i=1}^{N} \epsilon_{i} \frac{N\left(\theta_{m}^{(t)}+\epsilon_{i}, \mathcal{A}\right)+F\left(\theta_{m}^{(t)}+\epsilon_{i}\right)}{2} \\

NSRAdapt-ES (NSRA-ES)

自适应的权重参数初始值为 w=1.0。如果算法的性能经过了很多代之后没有变化，我们就开始降低 w。然后，当性能开始提升时，我们停止降低 w，反而增大 w。这样一来，当性能停止提升时，模型更偏向于提升适应度，而不是新颖性。

\theta_{m}^{(t+1)} \leftarrow \theta_{m}^{(t)}+\alpha \frac{1}{\sigma} \sum_{i=1}^{N} \epsilon_{i}\left(w N\left(\theta_{m}^{(t)}+\epsilon_{i}, \mathcal{A}\right)+(1-w) F\left(\theta_{m}^{(t)}+\epsilon_{i}\right)\right) \\

Improving Exploration in Evolution Strategies for Deep Reinforcement Learning via a Population of Novelty-Seeking Agents

CEM-RL

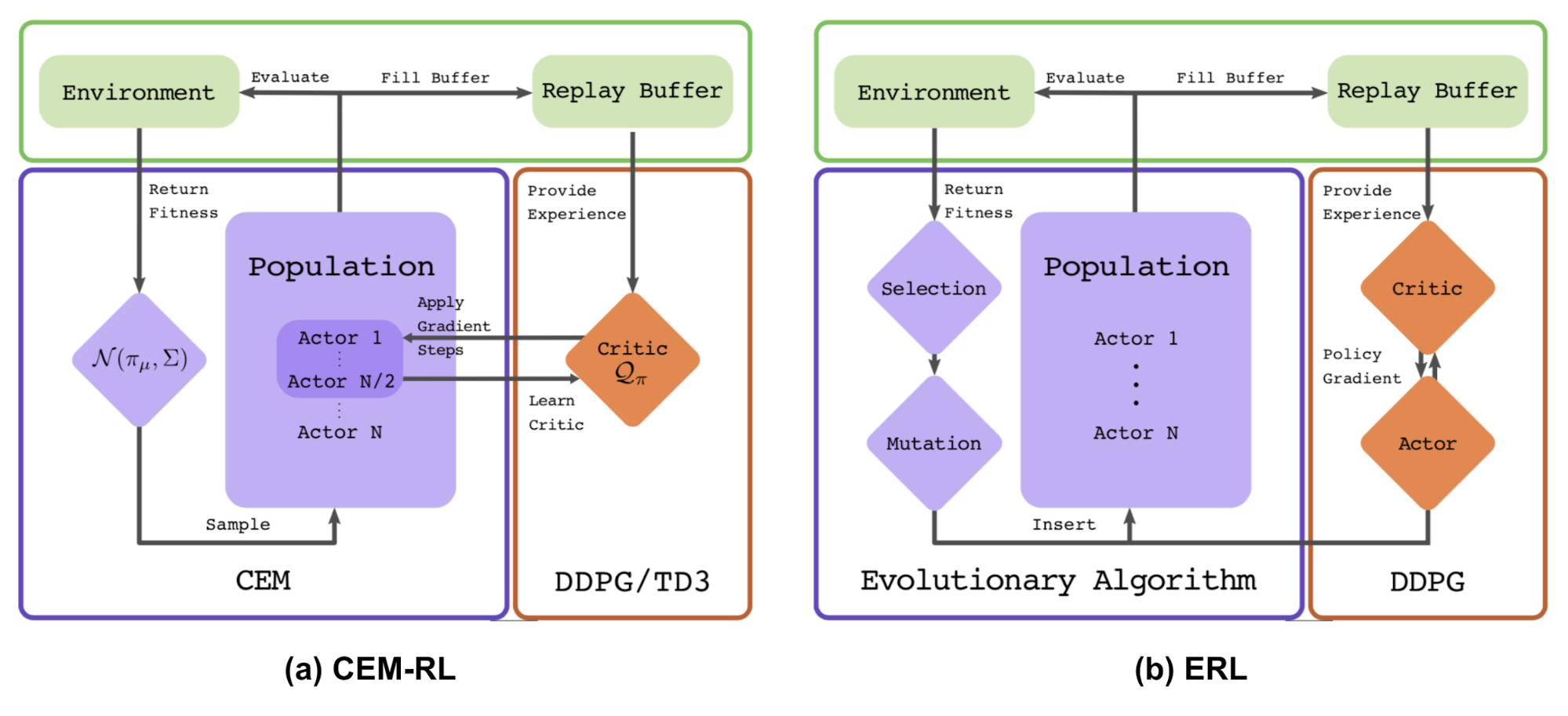
CEM-RL 方法结合了交叉熵方法（CEM）和 DDPG 或 TD3。

在这里，CEM 的工作原理与上面介绍的简单高斯演化策略基本相同，因此可以使用 CMA-ES 替换相同的函数。CEM-RL 是基于演化强化学习（ERL，详见 Khadka 和 Tumer 等人于 2018 年发表的论文Evolution-Guided Policy Gradient in Reinforcement Learning）的框架构建的，它使用标准的演化算法选择并演化「Actor」的种群。随后，在这个过程中生成的首次展示经验也会被加入到经验回放池中，用于训练强化学习的「Actor」网络和「Critic」网络。

工作流程：

π_μ 为 CEM 种群的「Actor」平均值，使用随机的「Actor」网络对其进行初始化。
「Critic」网络 Q 也将被初始化，通过 DDPG/TD3 算法对其进行更新。
重复以下步骤直到满足要求：

在分布 N (π_μ,Σ) 上采样得到一个「Actor」的种群。
评估一半「Actor」的种群。将适应度得分用作累积奖励 R，并将其加入到经验回放池中。
将另一半「Actor」种群与「Critic」一同更新。
使用性能最佳的优秀样本计算出新的π_mu 和 Σ。也可以使用 CMA-ES 进行参数更新。

拓展：深度学习中的演化算法

演化算法已经被应用于各种各样的深度学习问题中。「POET」（详见 Wang 等人于 2019 年发表的论文「Paired Open-Ended Trailblazer (POET): Endlessly Generating Increasingly Complex and Diverse Learning Environments and Their Solutions」）就是一种基于演化算法的框架，它试图在解决问题的同时生成各种各样不同的任务。

另一个例子则是演化强化学习（ERL)。

下面，我将更详细地介绍两个应用实例：基于种群的训练（PBT），以及权重未知的神经网络（WANN）

1、超参数调优：PBT

Population Based Training of Neural Networks

基于种群的训练（PBT，详见 Jaderberg 等人于 2017 年发表的论文「Population Based Training of Neural Networks」）将演化算法应用到了超参数调优问题中。它同时训练了一个模型的种群以及相应的超参数，从而得到最优的性能。

PBT 过程起初拥有一组随机的候选解，它们包含一对模型权重的初始值和超参数 {(θ_i,h_i)∣i=1,…,N}。我们会并行训练每个样本，然后周期性地异步评估其自身的性能。当一个成员准备好后（即该成员进行了足够的梯度更新步骤，或当性能已经足够好），就有机会通过与整个种群进行对比进行更新：

「exploit ()」：当模型性能欠佳时，可以用性能更好的模型的权重来替代当前模型的权重。
「explore ()」：如果模型权重被重写，「explore」步骤会使用随机噪声扰动超参数。

在这个过程中，只有性能良好的模型和超参数对会存活下来，并继续演化，从而更好地利用计算资源。

网络拓扑优化：WANN

权重未知的神经网络（WANN，详见 Gaier 和 Ha 等人于 2019 年发表的论文「Weight Agnostic Neural Networks」）在不训练网络权重的情况下，通过搜索最小的网络拓扑来获得最优性能。

由于不需要考虑网络权值的最佳配置，WANN 更加强调网络架构本身，这使得它的重点与神经网络架构搜索（NAS）不同。WANN 在演化网络拓扑的时候深深地受到了一种经典的遗传算法「NEAT」（增广拓扑的神经演化，详见 Stanley 和 Miikkulainen 等人于 2002 年发表的论文「Efficient Reinforcement Learning through Evolving Neural Network Topologies」）的启发。

WANN 的工作流程看上去与标准的遗传算法基本一致：

初始化：创建一个最小网络的种群。
评估：使用共享的权重值进行测试。
排序和选择：根据性能和复杂度排序。
变异：通过改变最佳的网路来创建新的种群。

在「评估」阶段，我们将所有网络权重设置成相同的值。这样一来，WANN 实际上是在寻找可以用最小描述长度来描述的网络。在「选择」阶段，我们同时考虑网络连接和模型性能。

WANN 的结果是同时使用随机权重和共享权重（单一权重）评估得到的。有趣的是，即使在对所有权重执行权重共享并对于这单个参数进行调优的时候，WANN 也可以发现实现非常出色的性能的拓扑。

参考文献

[1] Nikolaus Hansen. “The CMA Evolution Strategy: A Tutorial” arXiv preprint arXiv:1604.00772 (2016).

[2] Marc Toussaint. Slides: “Introduction to Optimization”

[3] David Ha. “A Visual Guide to Evolution Strategies” blog.otoro.net. Oct 2017.

[4] Daan Wierstra, et al. “Natural evolution strategies.” IEEE World Congress on Computational Intelligence, 2008.

[5] Agustinus Kristiadi. “Natural Gradient Descent” Mar 2018.

[6] Razvan Pascanu & Yoshua Bengio. “Revisiting Natural Gradient for Deep Networks.” arXiv preprint arXiv:1301.3584 (2013).

[7] Tim Salimans, et al. “Evolution strategies as a scalable alternative to reinforcement learning.” arXiv preprint arXiv:1703.03864 (2017).

[8] Edoardo Conti, et al. “Improving exploration in evolution strategies for deep reinforcement learning via a population of novelty-seeking agents.” NIPS. 2018.

[9] Aloïs Pourchot & Olivier Sigaud. “CEM-RL: Combining evolutionary and gradient-based methods for policy search.” ICLR 2019.

[10] Shauharda Khadka & Kagan Tumer. “Evolution-guided policy gradient in reinforcement learning.” NIPS 2018.

[11] Max Jaderberg, et al. “Population based training of neural networks.” arXiv preprint arXiv:1711.09846 (2017).

[12] Adam Gaier & David Ha. “Weight Agnostic Neural Networks.” arXiv preprint arXiv:1906.04358 (2019).

发布于 2020-06-27 10:43

深度学习（Deep Learning）

自然进化

强化学习 (Reinforcement Learning)

进化策略及其在深度学习中的应用