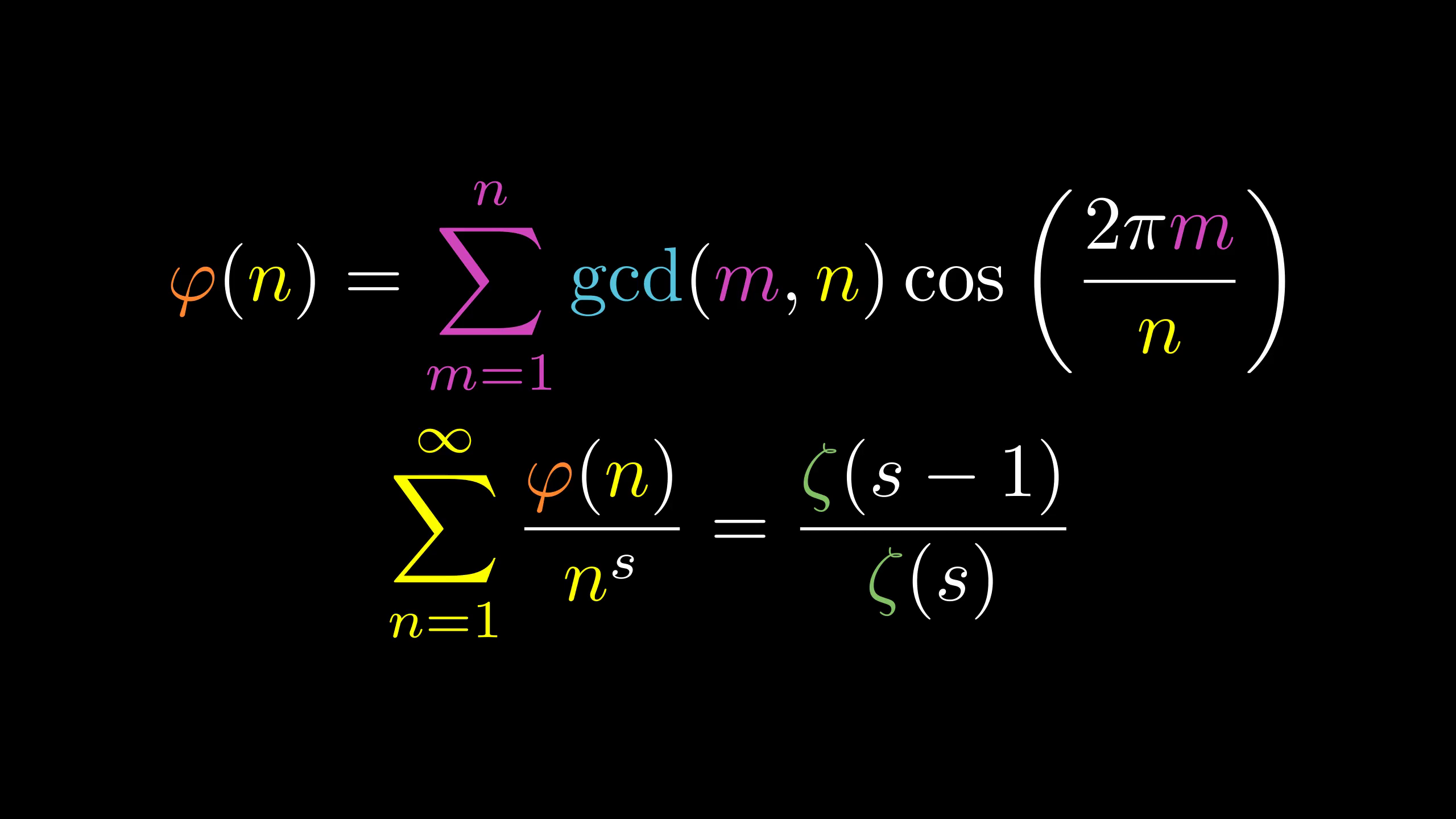当数论遇上分析——拉马努金和与欧拉函数的故事
从DFT到拉马努金和
定义数论函数 f:\mathbb Z^+\mapsto\mathbb C,n\mapsto f(n) ,设其离散Fourier变换为F(n,k),则有:
F(n,k)=\sum_{m=1}^nf(\gcd(m,n))e^{-2\pi ikm/n}
光留着这个表达式也不是个滋味儿,我们不妨利用gcd重排一下求和:
事实上,所有满足 \gcd(m,n)=d 的m都满足 m=jd 且 1\le j\le n/d,\gcd(j,n/d)=1 。而又因为 d|n ,我们的求和式可以被改写成:
F(n,k)=\sum_{d|n}f(d)\sum_{j=1,\gcd(j,n/d)=1}^{n/d}e^{-2\pi ikjd/n }
现在定义函数 c_n(k)\equiv\sum_{j=1,\gcd(j,n)=1}^ne^{-2\pi ijk/n} ,则原式等于:
F(n,k)=\sum_{d|n}f(d)c_{n/d}(k)\equiv(f*c_\bullet(k))(n)\tag1
所以其实这种特殊的DFT可以被转化为Dirichlet卷积。而 c_n(k) 被称为拉马努金和(Ramanujan sum)。
拉马努金和的性质
1、对称性: c_n(k)=c_n(-k)
证明:事实上根据 \forall h\in\mathbb Z,e^{2\pi ih}=1 有:
c_n(k)=e^{2\pi ik}g_k(n)=\sum_{j=1,\gcd(j,n)=1}^ne^{2\pi i(n-j)k/n}
现在我们更改求和顺序 j\mapsto n-j ,得:
c_n(k)=\sum_{j=0,\gcd(n-j,n)=1}^{n-1}e^{2\pi jk/n}
由于 \gcd(n,n)=\gcd(0,n)=n\ne1 ,j的范围可以改为 1\le j\le n ,又因为 \gcd(n-j,n)=\gcd(j,n) ,我们有:
c_n(k)=\sum_{j=1,\gcd(j,n)=1}^n e^{-2\pi ij(-k)/n}=c_n(-k)
证毕
由拉马努金和的对称性可知 \Im(g_k(n))\equiv0 ,因此可以改写成 c_n(k)=\sum_{j=1,\gcd(j,n)=1}^n\cos\left(2\pi jk\over n\right)
2、 c_n(k)=\sum_{d|\gcd(k,n)}\mu\left(\frac nd\right)d
证明:根据莫比乌斯反演公式,有 \sum_{d|n}\mu(d)=(1*\mu)(n)=[n=1] [1],因此有:
\begin{aligned} c_n(k) &=\sum_{j=1}^n e^{2\pi ijk/n}[\gcd(j,n)=1]=\sum_{j=1}^n\sum_{d|\gcd(j,n)}\mu(d)e^{2\pi ijk/n}=\sum_{j=1}^n\sum_{d|\gcd(j,n)}\mu(d)e^{2\pi i(j/d)k/(n/d)} \end{aligned}
由 d|\gcd(j,n) 可知 j/d,n/d\in\mathbb Z 。因此令 h=j/d 可得:
c_n(k)=\sum_{d|\gcd(hd,n)}\sum_{h=1}^{n/d}\mu(d)e^{2\pi ihk/(n/d)}=\sum_{d|n}\mu(d)\sum_{h=1}^{n/d}e^{2\pi ihk/(n/d)}\tag a
为了解决最后一个求和式,我们要研究一下求和式 \sum_{h=1}^me^{2\pi iht/m} 的性质:
当 m|t 时原式为 \sum_{h=1}^m1=m ,而当 m\nmid t 时根据 \sum_{h=1}^mw^h=w\cdot{w^m-1\over w-1} 有:
\sum_{h=1}^me^{2\pi iht/m}=e^{2\pi it/m}{e^{2\pi it}-1\over e^{2\pi it/m}-1}=0
因此 \sum_{h=1}^me^{2\pi iht/m}=m[m|t] ,代入回(a)式可得:
c_n(k)=\sum_{d|n}\mu(d)(n/d)[(n/d)|k]=\sum_{d|n}\mu\left(\frac nd\right)d[d|k]=\sum_{d|n\wedge d|k}\mu\left(\frac nd\right)d
根据最大公因数的定义,可知 d|n\wedge d|k\iff d|\gcd(k,n) ,于是:
c_n(k)=\sum_{d|\gcd(k,n)}\mu\left(\frac nd\right)d
证毕
这个结果的一个显然推论是 c_n(1)=\mu(n) ,于是:
\mu(n)=\sum_{j=1,\gcd(j,n)=1}^n\cos\left(2\pi j\over n\right)\tag2
事实上拉马努金和也可以帮助我们研究欧拉函数的性质
3、 c_n(0)=\varphi(n)
证明:由 c_n(0)=\sum_{j=1,\gcd(j,n)=1}^n1 可知 c_n(0) 刚好计算的是n以内与n互素数的数量,即 \varphi(n)
因为 \gcd(0,n)=\gcd(n,n)=1 ,所以根据性质2有 c_n(0)=\sum_{d|n}\mu\left(\frac nd\right)d 。又根据 c_n(0)=\varphi(n) 可知 \varphi(n)=\sum_{d|n}\mu\left(\frac nd\right)d 。
欧拉函数与Fourier变换
现在设 \operatorname{id}(n)\equiv n 则有 \varphi(n)=(\operatorname{id}*\mu)(n) 事实上根据(1)式和 c_n(1)=\mu(n) ,有:
\varphi(n)=\sum_{m=1}^n\operatorname{id}(\gcd(m,n))e^{-2\pi im/n}=\sum_{m=1}^n\gcd(m,n)\cos\left(2\pi m\over n\right)\tag3
这个公式允许我们在不对n进行分解的情况下计算 \varphi(n) 。
欧拉函数与Zeta函数
根据Dirichlet级数的性质 \sum_{n=1}^\infty{a(n)\over n^s}\sum_{k=1}^\infty{b(k)\over k^s}=\sum_{n=1}^\infty{(a*b)(n)\over n^s} ,有:
\sum_{n=1}^\infty{\varphi(n)\over n^s}=\sum_{n=1}^\infty{(n*\mu)(n)\over n^s}=\sum_{n=1}{1\over n^{s-1}}\sum_{n=1}^\infty{\mu(n)\over n^s}
引入 \zeta(s)\equiv\sum_{n=1}^\infty{1\over n^s}\Rightarrow{1\over\zeta(s)}=\sum_{n=1}^\infty{\mu(n)\over n^s} [2],可得:
\sum_{n=1}^\infty{\varphi(n)\over n^s}={\zeta(s-1)\over\zeta(s)}
这意味着:
\begin{aligned} \zeta(s-1) &=\zeta(s)\sum_{n=1}^\infty{\varphi(n)\over n^s} \cr &=\zeta(s)\sum_{n=1}^\infty\sum_{k=1}^n{1\over n^s}\gcd(k,n)e^{-2\pi ik/n} \end{aligned}
因此当有人拿出Zeta函数偶数值的计算公式装13时:
\sum_{k=1}^\infty{1\over k^{2m}}={B_{2m}(-1)^{m-1}(2\pi)^{2m}\over2(2m)!}
你便可以用Zeta函数奇数值公式回怼(doge:
\sum_{k=1}^\infty{1\over k^{2m-1}}={B_{2m}(-1)^{m-1}(2\pi)^{2m}\over2(2m)!}\sum_{n=1}^\infty\sum_{k=1}^n{\gcd(k,n)\over n^{2m}}e^{-2\pi ik/n}
事实上拉马努金和的应用远远不止这点。这篇文章的结尾目前比较草率。作者在完成更多相关的学习后会不断对本篇文章的内容进行补充。
参考
- ^若a为真[a]=1若a为假则[a]=0
- ^读懂黎曼猜想(1)——莫比乌斯反演 - 知乎 https://zhuanlan.zhihu.com/p/151302308