【学渣的自我修养】麦克纳姆轮浅谈
什么是麦克纳姆轮
在竞赛机器人和特殊工种机器人中,全向移动经常是一个必需的功能。「全向移动」意味着可以在平面内做出任意方向平移同时自转的动作。为了实现全向移动,一般机器人会使用「全向轮」(Omni Wheel)或「麦克纳姆轮」(Mecanum Wheel)这两种特殊轮子。
全向轮:

全向轮与麦克纳姆轮的共同点在于他们都由两大部分组成:轮毂和辊子(roller)。轮毂是整个轮子的主体支架,辊子则是安装在轮毂上的鼓状物。全向轮的轮毂轴与辊子转轴相互垂直,而麦克纳姆轮的轮毂轴与辊子转轴呈 45° 角。理论上,这个夹角可以是任意值,根据不同的夹角可以制作出不同的轮子,但最常用的还是这两种。
全向轮与麦克纳姆轮(以下简称「麦轮」)在结构、力学特性、运动学特性上都有差异,其本质原因是轮毂轴与辊子转轴的角度不同。经过分析,二者的运动学和力学特性区别可以通过以下表格来体现。

近年来,麦轮的应用逐渐增多,特别是在 Robocon、FRC 等机器人赛事上。这是因为麦克纳姆轮可以像传统轮子一样,安装在相互平行的轴上。而若想使用全向轮完成类似的功能,几个轮毂轴之间的角度就必须是 60°,90° 或 120° 等角度,这样的角度生产和制造起来比较麻烦。所以许多工业全向移动平台都是使用麦克纳姆轮而不是全向轮,比如这个国产的叉车: 全向移动平台 麦克纳姆轮叉车 美科斯叉车
另外一个原因,可能是麦轮的造型比全向轮要酷炫得多,看起来有一种不明觉厉的感觉……
麦轮的安装方法
麦轮一般是四个一组使用,两个左旋轮,两个右旋轮。左旋轮和右旋轮呈手性对称,区别如下图。

- X-正方形:轮子转动产生的力矩会经过同一个点,所以 yaw 轴无法主动旋转,也无法主动保持 yaw 轴的角度。一般几乎不会使用这种安装方式。
- X-长方形:轮子转动可以产生 yaw 轴转动力矩,但转动力矩的力臂一般会比较短。这种安装方式也不多见。
- O-正方形:四个轮子位于正方形的四个顶点,平移和旋转都没有任何问题。受限于机器人底盘的形状、尺寸等因素,这种安装方式虽然理想,但可遇而不可求。
- O-长方形:轮子转动可以产生 yaw 轴转动力矩,而且转动力矩的力臂也比较长。是最常见的安装方式。
麦轮底盘的正逆运动学模型
以O-长方形的安装方式为例,四个轮子的着地点形成一个矩形。正运动学模型(forward kinematic model)将得到一系列公式,让我们可以通过四个轮子的速度,计算出底盘的运动状态;而逆运动学模型(inverse kinematic model)得到的公式则是可以根据底盘的运动状态解算出四个轮子的速度。需要注意的是,底盘的运动可以用三个独立变量来描述:X轴平动、Y轴平动、yaw 轴自转;而四个麦轮的速度也是由四个独立的电机提供的。所以四个麦轮的合理速度是存在某种约束关系的,逆运动学可以得到唯一解,而正运动学中不符合这个约束关系的方程将无解。
先试图构建逆运动学模型,由于麦轮底盘的数学模型比较复杂,我们在此分四步进行:
①将底盘的运动分解为三个独立变量来描述;
②根据第一步的结果,计算出每个轮子轴心位置的速度;
③根据第二步的结果,计算出每个轮子与地面接触的辊子的速度;
④根据第三部的结果,计算出轮子的真实转速。
一、底盘运动的分解
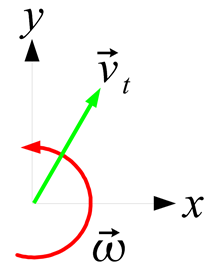
我们知道,刚体在平面内的运动可以分解为三个独立分量:X轴平动、Y轴平动、yaw 轴自转。如下图所示,底盘的运动也可以分解为三个量:
v_{t_x} 表示 X 轴运动的速度,即左右方向,定义向右为正;
v_{t_y} 表示 Y 轴运动的速度,即前后方向,定义向前为正;
\vec{\omega} 表示 yaw 轴自转的角速度,定义逆时针为正。
以上三个量一般都视为四个轮子的几何中心(矩形的对角线交点)的速度。
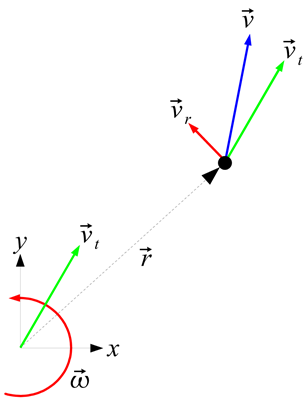
二、计算出轮子轴心位置的速度
定义:
\vec{r} 为从几何中心指向轮子轴心的矢量;
\vec{v} 为轮子轴心的运动速度矢量;
\vec{v_r} 为轮子轴心沿垂直于 \vec{r} 的方向(即切线方向)的速度分量;
那么可以计算出:
分别计算 X、Y 轴的分量为:
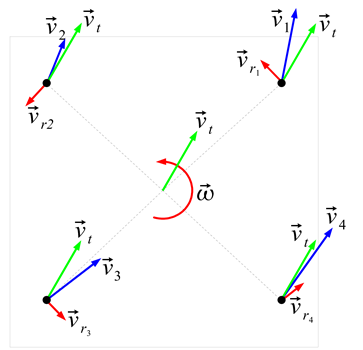
三、计算辊子的速度
根据轮子轴心的速度,可以分解出沿辊子方向的速度 \vec{v_\|} 和垂直于辊子方向的速度 \vec{v_\perp} 。其中 \vec{v_\perp} 是可以无视的(思考题:为什么垂直方向的速度可以无视?),而
\vec{v_\|}=\vec{v} \cdot \hat{u}=(v_x\hat{i}+v_y\hat{j})\cdot(-\frac{1}{\sqrt{2}}\hat{i}+\frac{1}{\sqrt{2}}\hat{j})=-\frac{1}{\sqrt{2}}v_x+\frac{1}{\sqrt{2}}v_y其中 \hat{u} 是沿辊子方向的单位矢量。

四、计算轮子的速度
从辊子速度到轮子转速的计算比较简单:
v_w=\frac{v_\|}{cos 45^\circ}=\sqrt{2}(-\frac{1}{\sqrt{2}}v_x+\frac{1}{\sqrt{2}}v_y)=-v_x+v_y结合以上四个步骤,可以根据底盘运动状态解算出四个轮子的转速:
\begin{equation} \begin{cases} v_{w_1}=v_{t_y}-v_{t_x}+\omega(a+b) \\ v_{w_2}=v_{t_y}+v_{t_x}-\omega(a+b) \\ v_{w_3}=v_{t_y}-v_{t_x}-\omega(a+b) \\ v_{w_4}=v_{t_y}+v_{t_x}+\omega(a+b) \\ \end{cases} \end{equation}以上方程组就是O-长方形麦轮底盘的逆运动学模型,而正运动学模型可以直接根据逆运动学模型中的三个方程解出来,此处不再赘述。
另一种计算方式
「传统」的推导过程虽然严谨,但还是比较繁琐的。这里介绍一种简单的逆运动学计算方式。
我们知道,全向移动底盘是一个纯线性系统,而刚体运动又可以线性分解为三个分量。那么只需要计算出麦轮底盘在「沿X轴平移」、「沿Y轴平移」、「绕几何中心自转」时,四个轮子的速度,就可以通过简单的加法,计算出这三种简单运动所合成的「平动+旋转」运动时所需要的四个轮子的转速。而这三种简单运动时,四个轮子的速度可以通过简单的测试,或是推动底盘观察现象得出。
当底盘沿着 X 轴平移时:
\begin{equation} \begin{cases} v_{w_1}=-v_{t_x} \\ v_{w_2}=+v_{t_x} \\ v_{w_3}=-v_{t_x} \\ v_{w_4}=+v_{t_x} \\ \end{cases} \end{equation}当底盘沿着 Y 轴平移时:
当底盘绕几何中心自转时:
将以上三个方程组相加,得到的恰好是根据「传统」方法计算出的结果。这种计算方式不仅适用于O-长方形的麦轮底盘,也适用于任何一种全向移动的机器人底盘。
Makeblock 麦轮底盘的组装
理论分析完成,可以开始尝试将其付诸实践了。
第一步,组装矩形框架。

第二步,组装电机模块。
由于麦轮底盘的四个轮子速度有约束关系,必须精确地控制每个轮子的速度,否则将会导致辊子与地面发生滑动摩擦,不仅会让底盘运动异常,还会让麦轮的寿命减少。所以必须使用编码电机。

第五步,安装电路板并接线。
编码电机必须配上相应的驱动板才能正常工作。这里使用的 Makeblock 编码电机驱动板,每一块板可以驱动两个电机。接线顺序在下文中会提及,也可以随意接上,在代码中定义好对应的顺序即可。

至此,一个能独立运行的麦轮底盘就完成了。
控制程序
根据麦轮的底盘的运动学模型,要完全控制它的运动,需要有三个控制量:X轴速度、Y轴速度、自转角速度。要产生这三个控制量,有很多种方法,本文将使用一个 USB 游戏手柄,左边的摇杆产生平移速度,右边的摇杆产生角速度。
首先将一个 USB Host 模块连接到 Orion 主板的 3 口。
#include <Wire.h>
#include <SoftwareSerial.h>
#include "MeOrion.h"
MeUSBHost joypad(PORT_3);
// 手柄代码(红灯亮模式)
// 默认:128-127-128-127-15-0-0-128
// 左一:128-127-128-127-15-1-0-128
// 右一:128-127-128-127-15-2-0-128
// 左二:128-127-128-127-15-4-0-128
// 右二:128-127-128-127-15-8-0-128
// 三角:128-127-128-127-31-0-0-128 (0001 1111)
// 方形:128-127-128-127-143-0-0-128 (1000 1111)
// 叉号:128-127-128-127-79-0-0-128 (0100 1111)
// 圆圈:128-127-128-127-47-0-0-128 (0010 1111)
// 向上:128-127-128-127-0-0-0-128 (0000 0000)
// 向下:128-127-128-127-4-0-0-128 (0000 0100)
// 向左:128-127-128-127-6-0-0-128 (0000 0110)
// 向右:128-127-128-127-2-0-0-128 (0000 0010)
// 左上:128-127-128-127-7-0-0-128 (0000 0111)
// 左下:128-127-128-127-5-0-0-128 (0000 0101)
// 右上:128-127-128-127-1-0-0-128 (0000 0001)
// 右下:128-127-128-127-3-0-0-128 (0000 0011)
// 选择:128-127-128-127-15-16-0-128
// 开始:128-127-128-127-15-32-0-128
// 摇杆:右X-右Y-左X-左Y-15-0-0-128
MeEncoderMotor motor1(0x02, SLOT2);
MeEncoderMotor motor2(0x02, SLOT1);
MeEncoderMotor motor3(0x0A, SLOT2);
MeEncoderMotor motor4(0x0A, SLOT1);
// 底盘:a = 130mm, b = 120mm
float linearSpeed = 100;
float angularSpeed = 100;
float maxLinearSpeed = 200;
float maxAngularSpeed = 200;
float minLinearSpeed = 30;
float minAngularSpeed = 30;
void setup()
{
// 要上电才能工作,不能只是插上 USB 线来调试。
motor1.begin();
motor2.begin();
motor3.begin();
motor4.begin();
Serial.begin(57600);
joypad.init(USB1_0);
}
void loop()
{
Serial.println("loop:");
//setEachMotorSpeed(100, 50, 50, 100);
if(!joypad.device_online)
{
// 若一直输出离线状态,重新拔插 USB Host 的 RJ25 线试一下。
Serial.println("Device offline.");
joypad.probeDevice();
delay(1000);
}
else
{
int len = joypad.host_recv();
parseJoystick(joypad.RECV_BUFFER);
delay(5);
}
//delay(500);
}
void setEachMotorSpeed(float speed1, float speed2, float speed3, float speed4)
{
motor1.runSpeed(speed1);
motor2.runSpeed(-speed2);
motor3.runSpeed(-speed3);
motor4.runSpeed(-speed4);
}
void parseJoystick(unsigned char *buf) //Analytic function, print 8 bytes from USB Host
{
// 输出手柄的数据,调试用
// int i = 0;
// for(i = 0; i < 7; i++)
// {
// Serial.print(buf[i]); //It won't work if you connect to the Makeblock Orion.
// Serial.print('-');
// }
// Serial.println(buf[7]);
// delay(10);
// 速度增减
switch (buf[5])
{
case 1:
linearSpeed += 5;
if (linearSpeed > maxLinearSpeed)
{
linearSpeed = maxLinearSpeed;
}
break;
case 2:
angularSpeed += 5;
if (angularSpeed > maxAngularSpeed)
{
angularSpeed = maxAngularSpeed;
}
break;
case 4:
linearSpeed -= 5;
if (linearSpeed < minLinearSpeed)
{
linearSpeed = minLinearSpeed;
}
break;
case 8:
angularSpeed -= 5;
if (angularSpeed < minAngularSpeed)
{
angularSpeed = minAngularSpeed;
}
break;
default:
break;
}
if ((128 != buf[0]) || (127 != buf[1]) || (128 != buf[2]) || (127 != buf[3]))
{
// 处理摇杆
float x = ((float)(buf[2]) - 127) / 128;
float y = (127 - (float)(buf[3])) / 128;
float a = (127 - (float)(buf[0])) / 128;
mecanumRun(x * linearSpeed, y * linearSpeed, a * angularSpeed);
}
else
{
switch (buf[4])
{
case 0:
mecanumRun(0, linearSpeed, 0);
break;
case 4:
mecanumRun(0, -linearSpeed, 0);
break;
case 6:
mecanumRun(-linearSpeed, 0, 0);
break;
case 2:
mecanumRun(linearSpeed, 0, 0);
break;
case 7:
mecanumRun(-linearSpeed/2, linearSpeed/2, 0);
break;
case 5:
mecanumRun(-linearSpeed/2, -linearSpeed/2, 0);
break;
case 1:
mecanumRun(linearSpeed/2, linearSpeed/2, 0);
break;
case 3:
mecanumRun(linearSpeed/2, -linearSpeed/2, 0);
break;
default:
mecanumRun(0, 0, 0);
break;
}
}
}
void mecanumRun(float xSpeed, float ySpeed, float aSpeed)
{
float speed1 = ySpeed - xSpeed + aSpeed;
float speed2 = ySpeed + xSpeed - aSpeed;
float speed3 = ySpeed - xSpeed - aSpeed;
float speed4 = ySpeed + xSpeed + aSpeed;
float max = speed1;
if (max < speed2) max = speed2;
if (max < speed3) max = speed3;
if (max < speed4) max = speed4;
if (max > maxLinearSpeed)
{
speed1 = speed1 / max * maxLinearSpeed;
speed2 = speed2 / max * maxLinearSpeed;
speed3 = speed3 / max * maxLinearSpeed;
speed4 = speed4 / max * maxLinearSpeed;
}
setEachMotorSpeed(speed1, speed2, speed3, speed4);
}
大功告成: