机器学习文献翻译及注解（2）--SVM的SMO算法（John Platt 1998）

Sequential Minimal Optimization:A Fast Algorithm for Training Support Vector Machines

摘要
1 introduction
1.1 SVM概述
1.2 之前的SVM算法
2 SMO
2.1 两个拉格朗日乘数的解法
2.2 选择待优化的乘数的启发式方法
2.3 计算阈值
2.4 线性SVM的优化
2.5 代码详细
2.6 和之前算法的关系
3 Benchmarking SMO
4 结论
单词、短语

Sequential Minimal Optimization:

A Fast Algorithm for Training Support Vector Machines

John C. Platt

Microsoft Research

jplatt@microsoft.com

Technical Report MSR-TR-98-14

April 21, 1998

© 1998 John Platt

摘要

本文提出一种新的训练支持向量机的算法：序贯最小优化（SMO，最小优化表示每次优化的时候只优化两个拉格朗日乘数，每个拉格朗日乘数对应工作集（working set）中的一个点，也就是说每次优化的工作集中只有两个样本，此为最小）。训练一个SVM需要解一个非常大（即变量个数非常多）的二次方程（QP问题）。SMO将这个大QP问题分解为一系列小到不能再小的QP问题。这些小QP问题可以得到解析解，而且解的过程避免了耗时的QP数值优化作为内循环。SMO需要的内存大小随训练集的大小线性增长，这就允许SMO处理很大的训练集。因为避免了矩阵计算，SMO的计算复杂度在多个测试问题（一些经典的问题及数据集）上介于O（训练集大小）和O（训练集大小的二次方）之间，而标准的分组SVM算法的计算复杂度则介于O（训练集大小）和O（训练集大小的三次方）之间。SMO的计算时间取决于SVM evaluation,（不知道怎么翻译，从上下文看指的是计算复杂度），因此SMO对线性SVM和稀疏数据集来说是最快的。在真实世界里的稀疏数据集上，SMO可以比分组SVM算法快1000倍。

1 introduction

在过去的几年里，涌起了一股了解SVM的风潮，SVM已经经验性地表明了在一系列广阔的问题上（比如手写字符识别、面部识别、行人识别和文本分类）具有很好的泛化能力。

然而SVM的使用仍然局限于一小群研究者之间。一个可能的原因是SVM训练起来很慢，尤其对于大型问题。另外一个原因是SVM训练算法对一般工程师来说实现起来太复杂、太难。

本文描述了一种新的SVM学习算法，概念清晰、实现简单、通常情况下更快，而且比标准的SVM算法在困难的SVM问题上有更好的scaling properties（不知道怎么翻译，结合摘要部分，应该指计算复杂度，即当问题规模增大scale时，计算难度没有增大scale过快）。新的SVM算法称作序贯最小优化算法，不像之前的SVM算法使用数值二次规划作为内循环，SMO使用解析二次规划步。

本文首先描述一下SVM的全貌和当前的SVM算法，然后详细介绍SMO算法，包括二次规划步的解析解、在内循环里选择做优化的变量的启发式方法、如何设置SVM的阈值、某些特例的优化、算法的伪代码、SMO和其他算法的关系。

SMO已经在两个真实世界的数据集和两个人工数据集上做过测试。本文将展示SMO算法的运算时间和标准分组算法的运算时间对比。最后有个附录描述解析优化的推导过程。

1.1 SVM概述

Vladimir Vapnik在1979年发明了SVM，最简单的情形中，SVM是一个线性超平面，形式如下：

其中w是超平面的法向量，x是输入向量。分割超平面为u=0的超平面，离超平面最近的点在u=±1的超平面上，因此间隔m可表示为：

最大化间隔可以表示为如下最优化问题（参见文献4）：

其中xi是第i个训练样本，yi是对应的正确输出（1表示正例，-1表示反例）。

使用拉格朗日乘数，最优化问题可以转为一个对偶问题（一个QP问题），目标函数Ψ仅仅取决于一系列拉格朗日乘数αi

其中N是训练样本的个数，满足以下不等式约束：

以及一个线性等式约束：

拉格朗日乘数和训练样本有一对一的关系。一旦拉格朗日乘数确定了，法向量w和阈值b可以由拉格朗日乘数推导出来：

因为w可以通过（7）从训练数据中预先计算得出，估算一个SVM的计算量就是非零支持向量的个数。（Because w can be computed via equation (7) from the training data before use，为什么？即使如此，怎么得出后面的结论？）

当然，并不是所有的数据集都是线性可分的。在1995年Cortes和Vapnik（见文献7）建议对原始优化问题（见（3））做些修改，允许样本没有达到正确的间隔（即落在间隔内部），但要因此而对目标函数加一个惩罚。

其中εi就是为了样本允许落在间隔内而引入的松弛变量，C是平衡最大化间隔和最小化落在间隔内的样本个数的参数。当（8）转为对偶形式的时候，只有不等式约束（5）变成边界约束：

松弛变量εi并没有出现在对偶形式中。

SVM也可以推广到非线性分类中（见文献2）。一个非线性SVM的结果通过拉格朗日乘数直接计算得出：

其中K是核函数，用来度量输入向量x和存储的训练向量xj之间的相似度或距离。K的可选集包括高斯函数、多项式、非线性神经网络（见文献4）。如果K是线性的，SVM也是线性的（一个有意思的练习）。

拉格朗日乘数αi依然通过二次规划计算得出。非线性情况下二次规划形式改变，但对偶目标函数Ψ仍然是α的二次形式：

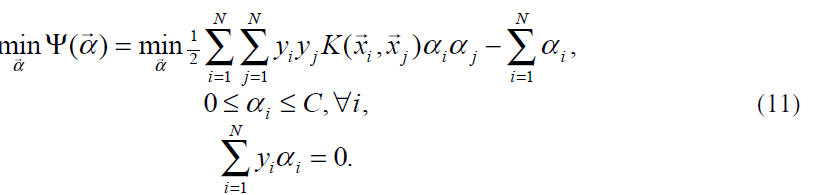
上述QP问题就是SMO算法将要解决的。为了使上述QP问题正定。核函数K必须遵守Mercer条件（见文献4）。

KKT条件是正定QP问题存在最优解的充要条件：

其中ui是第i个训练样本的SVM计算结果。注意到KKT条件一个样本计算一次，这对SMO算法的构造很有帮助。

1.2 之前的SVM算法

由于（11）所示的QP问题规模太大，通过标准的二次规划技术解决起来很难。（11）中包含一个矩阵，矩阵中有一些元素的值等于训练样本的个数的平方。这个矩阵在样本个数大于4000的时候将不小于128M。

Vapnik在文献19中提出了一个方法，被称为分组。分组算法利用以下事实：二次型的值在移除为0的拉格朗日乘数对应的行和列的时候保持不变。因此大的QP问题可以分解为一系列小的QP问题，最终目的是识别出所有的非零乘数、舍弃所有的零乘数。在每一步，分组算法解决一个包含如下样本的QP问题：上一步的所有非零乘数、违反KKT条件程度最多的M个样本（见文献4），以及某些M值（见图2）（什么叫某些M值？）。如果某一步违反KKT条件的样本少于M个，这些样本都被加进来。

图2（图中一条横线表示一次训练过程中的训练集，方框表示那次训练过程中的拉格朗日乘数。对于分组算法，每一次训练增加固定个数的样本、舍弃零乘数。因此训练样本逐步增加。Osuna的算法每一次训练中优化固定数目的样本，增加和删除样本的数目相同。SMO每次训练只优化两个样本，而且是计算解析解（而不是通过数值优化），因此非常快）

每个QP子问题都从上一个子问题的结果开始，在最后一步，所有非零拉格朗日乘数都被识别出，因此最后一步就解决了大QP问题。

分组明显地减少了矩阵的大小，从训练样本个数的平方降低到接近非零乘数个数的平方。但是分组仍然无法处理大型训练问题，因为瘦身后的矩阵仍然无法装进内存（估计当时的内存大小就是128M）。

1997年，Osuna等人（见文献16，也就是上一篇翻译的文献）证明了一个理论，为SVM提供了一套新的算法。这个理论证明大的QP问题可以分解为一系列小的QP子问题。只要每一步有一个违反KKT条件的样本被加入前一步的子问题的样本集（在文献16里面称之为工作集，即B）中，整体目标函数值就会降低且得到一个满足所有条件的可行解。因此逐步增加至少一个违反KKT条件的样本肯定能收敛。注意到分组算法也满足这个理论的条件，因此也会收敛（一个有意思的思考）。

Osuna等人建议对每个QP子问题保持矩阵大小恒定，这就意味着每一步增加和删除的样本数相同（见图2）。使用固定大小的矩阵允许在任意大小的数据集上进行训练。算法建议每一步增加和删除一个样本。显然这并不高效，因为他使用整个QP数值优化步来引起一个训练样本去满足KKT条件。在实践中，研究者增加和减少多个样本，根据未发布的启发式方法（见文献17，文献17 写着Osuna, E., Personal Communication，这是跟Osuna个人沟通的意思？个人沟通也可以作为文献23333）。在任何情况下，一个QP数值解法都需要上述所有的方法。数值解法众所周知很难得到正确的解法，有很多数值精度问题需要处理。

2 SMO

SMO是一个可以快速解决SVM QP问题而不使用矩阵存储空间和数值优化步的简单算法。SMO使用Osuna的理论分解QP问题以确保收敛。

不像之前的算法，SMO在每一步选择尽可能小的优化问题。对标准的SVM QP问题，最小的优化问题涉及到两个拉格朗日乘数，因为拉格朗日乘数必须遵循一个线性等式约束（也就意味着一个乘数可以通过剩下的乘数表示出来，固定n-1个乘数则剩下那个乘数也就确定了，没有优化的意义）。在每一步SMO选择两个乘数一起优化，寻找最优值，更新SVM体现这些新的最优值。

SMO的优势源于解那两个乘数的最优值的时候可以直接计算解析解，而不是通过数值优化。内层循环可以用一段很短的C代码表示，而不是调用整个QP运行库。尽管SMO需要解决更多子问题，但每个子问题的解决速度如此之快导致整体上看仍然更快。

此外，SMO不需要额外的空间存储矩阵。因此非常大规模的SVM训练问题也可以装进一台普通个人电脑的内存里。因为没有涉及到矩阵算法，SMO算法不受数值精度问题的影响。

SMO由两个部分组成：解那两个拉格朗日乘数的解析解和选择哪两个拉格朗日乘数进行优化的启发式算法。

2.1 两个拉格朗日乘数的解法

为了解那两个拉格朗日乘数，SMO首先计算这些拉格朗日乘数的约束条件然后解这些约束下的最小值。为了方便，所有涉及到第一个乘数的都有个下标1，第二个的有下标2。因为只有两个乘数，约束条件可以通过图1（应该是图3）方便地表示出来（因为都是二维空间）。边界约束（9）导致乘数位于一个盒子内，线性等式约束（6）导致乘数位于一条斜线上。因此目标函数在约束下的最小值一定位于一条斜线段上（见图3）。这个约束解释了为什么拉格朗日乘数可以被优化的最小数目是2：如果只优化一个乘数，不能在每次优化都满足线性等式约束。

图1（应该是图3）

线段的端点可以很简单地表示出来。不失一般性，算法首先计算第二个乘数α2并用

α2表示端点。如果y1不等于y2（每个乘数对应一个样本，y1、y2即样本的分类），则α2有以下边界：（根据等式约束6，y1和y2不等即一个为正一个为负，α1-α2+...=0）

如果y1等于y2，则α2有以下边界：

伴随斜线的第二个目标函数的衍生变量表示如下：

在正常情况下，目标函数将是正定的（为什么？），在线性等式约束的方向上将产生一个最小值（为什么正定能导致在等式约束上产生最小值？），η将大于0（η有啥含义？）。在这种情况下，SMO在约束的方向上的最小值如下：

其中Ei=ui-yi是第i个训练样本的误差。下一步，约束条件下的最小值通过在上述边界（14,15）进行截取获得：

现在，另s=y1y2，α1通过截取后的α2计算可得：

在特别情况下，η小于0，一个负的η将在核函数K不满足Mercer条件时出现，这导致目标函数变成不确定的（非正定）。如果超过一个训练样本有同样的输入向量x，一个正确的核函数也会导致η为0的情况出现。在任何情况下SMO都能工作，即使η不为正，这种情况下目标函数Ψ将在线段的两端计算得到：

SMO将移动乘数到端点（此处目标函数有最小值）。如果目标函数在两端取值相等（在一个小的舍入误差ε范围内）且核函数满足Mercer条件，那么优化将不再取得任何进展。这种场景下面会描述。

2.2 选择待优化的乘数的启发式方法

只要SMO每一步永远优化和改变两个乘数，且至少有一个乘数在优化前违反KKT条件，那么根据Osuna的理论每一步都能降低目标函数的值，也因此能保证收敛。为了加速收敛，SMO使用启发式方法来选择改变哪两个乘数。

有两个单独的启发式方法：一个选择第一个乘数，一个选择第二个乘数。选择第一个乘数的启发式方法提供SMO算法外层循环。外层循环首先在整个训练集上遍历，计算每个样本是否违反KKT条件（12），如果违反就可以用来优化（步骤1）。单次扫描整个训练集之后，外层循环遍历所有拉格朗日乘数不为0和C的样本（非边界样本），且每个样本都检查是否违反KKT条件，违反的将被用来做优化（步骤2）。外层循环扫描那些非边界样本直到所有的非边界样本在误差ε内满足KKT条件（什么意思？）。然后外层循环重新遍历训练集。外层循环交替进行在整个训练集上单次扫描和在非边界子集上多次扫描（步骤1和步骤2），直到整个训练集在误差ε内符合KKT条件，此时算法终止。（为什么扫描完整个训练集后再扫描非边界子集，不是个子集吗，不是已经被扫描过了吗？）

上述过程的CPU主要消耗在最可能违反KKT条件的样本上，即非边界子集（为什么？）。随着SMO算法的进行，边界的样本很可能仍然停留在边界上，但非边界样本则随着其他样本被优化而转移（为什么边界样本停留在边界上而非边界样本会移动？为什么会移动到自洽？）。SMO算法将遍历非边界子集直到子集自洽（什么叫子集自洽？）。然后SMO扫描整个数据集来查找任何由于优化非边界子集而违反KKT条件的边界样本（边界样本为什么）。

注意到检查是否违反KKT条件时使用了ε误差项，ε的经典取值为 10^{-3} 。识别系统一般来说并不需要以很高的精度去满足KKT条件，对处于正例边界的样本来说取值0.999到1.001之间都是可以接受的。如果不要求产生很高精度的结果，SMO算法（其他SVM算法也一样）就不会很快收敛。

一旦第一个乘数选定，SMO开始选择第二个乘数来最大化优化的步伐。现在，计算核函数很耗时间，所以SMO通过（16）中的|E1-E2|来估计步长。SMO为训练集的每一个非边界样本记录一个错误值E，然后选择一个错误值来估计最大步长。如果E1是正，SMO选择一个最小错误值E2；如果E1是负，SMO选择一个最大错误值E2.

在特殊情况下，SMO并不能通过上述第二个乘数的选择取得优化效果。举例来说，如果第一个和第二个训练样本有一样的输入变量x，这会导致目标函数编程半正定，就不会取得优化效果。在这种情况下，SMO在选择第二个乘数时有层次地使用启发式方法直到他找到一对能取得优化效果的乘数。在联合优化两个乘数时，如果有一个非零步长，就可以确定优化会取得效果。使用启发式方法选择第二个乘数时可以有以下层次：如果之前的启发式方法没有取得优化效果，SMO开始遍历非边界样本，寻找第二个可以取得优化效果的样本。如果非边界样本没有一个能取得优化效果，SMO开始遍历整个训练集直到找到一个能取得优化效果的样本。遍历非边界子集和遍历整个训练集都是随机选取起始位置，这是为了不使SMO偏好在数据集开始位置的样本。在极端环境下，可能找不到一个样本作为第二个合适的（能取得优化效果的）样本。这时第一个样本就被跳过，SMO重新选择一个样本。

2.3 计算阈值

阈值b在每一步之后都会重新计算，为了使得两个被优化的样本都满足KKT条件。在新的α1不在边界时，以下阈值b1有效，因为他能保证输入x1通过SVM计算输出y1：

同理：

当b1和b2都有效时他们是相等的。当两个新乘数都在边界上而且L不等于H时，b1和b2之间的值就是和KKT条件一致的阈值。SMO选择b1和b2的中间值作为阈值。

2.4 线性SVM的优化

为了计算线性SVM，只有一个权重向量w（而不是所有非零乘数对应的训练样本）需要被存储。如果联合优化成功，权重向量需要更新反映新的乘数。更新权重向量很容易，因为SVM的线性特性：

2.5 代码详细

以下伪代码描述了整个SMO算法：

target = desired output vector
point = training point matrix
procedure takeStep(i1,i2)
	if (i1 == i2) return 0
	alph1 = Lagrange multiplier for i1
	y1 = target[i1]
	E1 = SVM output on point[i1] – y1 (check in error cache)
	s = y1*y2
	Compute L, H via equations (13) and (14)
	if (L == H)
		return 0
	k11 = kernel(point[i1],point[i1])
	k12 = kernel(point[i1],point[i2])
	k22 = kernel(point[i2],point[i2])
	eta = k11+k22-2*k12
	if (eta > 0)
	{
		a2 = alph2 + y2*(E1-E2)/eta
		if (a2 < L) a2 = L
		else if (a2 > H) a2 = H
	}
	else
	{
		Lobj = objective function at a2=L
		Hobj = objective function at a2=H
		if (Lobj < Hobj-eps)
			a2 = L
		else if (Lobj > Hobj+eps)
			a2 = H
		else
			a2 = alph2
	}
	if (|a2-alph2| < eps*(a2+alph2+eps))
		return 0
	a1 = alph1+s*(alph2-a2)
	Update threshold to reflect change in Lagrange multipliers
	Update weight vector to reflect change in a1 & a2, if SVM is linear
	Update error cache using new Lagrange multipliers
	Store a1 in the alpha array
	Store a2 in the alpha array
	return 1
endprocedure

procedure examineExample(i2)
	y2 = target[i2]
	alph2 = Lagrange multiplier for i2
	E2 = SVM output on point[i2] – y2 (check in error cache)
	r2 = E2*y2
	if ((r2 < -tol && alph2 < C) || (r2 > tol && alph2 > 0))
	{
		if (number of non-zero & non-C alpha > 1)
		{
			i1 = result of second choice heuristic (section 2.2)
			if takeStep(i1,i2)
				return 1
		}
		loop over all non-zero and non-C alpha, starting at a random point
		{
			i1 = identity of current alpha
			if takeStep(i1,i2)
				return 1
		}
		loop over all possible i1, starting at a random point
		{
			i1 = loop variable
			if (takeStep(i1,i2)
				return 1
		}
	}
	return 0
endprocedure

main routine:
	numChanged = 0;
	examineAll = 1;
	while (numChanged > 0 | examineAll)
	{
		numChanged = 0;
		if (examineAll)
			loop I over all training examples
			numChanged += examineExample(I)
		else
			loop I over examples where alpha is not 0 & not C
			numChanged += examineExample(I)
		if (examineAll == 1)
			examineAll = 0
		else if (numChanged == 0)
			examineAll = 1
	}

2.6 和之前算法的关系

SMO算法和之前的SVM算法有关，SMO算法可以看做Osuna算法的一个特例：每次优化的样本大小是2而且每一步都通过启发式方法更新拉格朗日乘数。

SMO算法和叫做Bregman方法（见文献3）或行操作方法（见文献5）的优化算法家族有紧密关系。这些方法解决带线性约束的凸二次规划问题。他们都是迭代方法，每一步投射当前初始点到每一个约束条件上。原始的Bregman方法不能直接解决QP问题（见公式11），因为SVM的阈值导致对偶问题中有一个线性等式约束。如果每一步只规划一个约束，将不满足线性等式约束。用术语来说，在由所有带阈值b的权重向量的可能值组成的联合空间上最小化权重向量的取值范围这个主要问题产生了一个没有唯一最小值的Bregman D维投影（见文献3、6）。

考虑阈值b固定为0的SVM是很有意思的事。一个固定阈值的SVM不会有线性等式约束（6）。因此，每次只有一个乘数需要更新（可以通过一个行操作方法）。不幸的是，传统的Bregman方法由于（8）中的松弛变量的原因不适用于这样的SVM。松弛变量的存在导致Bregman D维投影在权重向量和松弛变量组成的空间里面不是唯一的。

幸运的是，SMO可以稍加修改用来解决固定阈值的SVM。SMO通过更新单个拉格朗日乘数来获得Ψ在对应维度上的最小值。更新规则如下：

这个更新公式强制SVM的输出为y1（类似于Bregman方法或Hildreth的QP方法（见文献10）。在计算出新的α之后，截断在[0,C]之间（不像之前的方法）。选择哪个乘数去优化和2.2部分描述的第一个启发式选择方法一样。

用来解决线性SVM的固定阈值的SMO在概念上类似于感知机松弛规则（见文献8），即感知机的输出在有误差的时候进行调整，以使输出正好位于间隔上。但是，固定阈值的SMO算法有时会减少训练输入在权重向量的占比以最大化间隔。这个松弛规则时常会增加训练输入在权重向量的数量，这不会最大化间隔。用高斯核函数的固定阈值的SMO也和资源分配网络算法（RAN，见文献18）有关。RAN检测某几种特定的误差，分配一个核函数来纠正这个误差。SMO也做相似的事。但SMO/SVM会调整核函数的高度（什么叫核函数的高度？the heights of the kernels）来在特征空间最大化间隔，而RAN只是简单地使用LMS来调整核函数的高度和宽度。

3 Benchmarking SMO

在几个问题（收入预测、网页分类、人造数据集）上的测试和性能对比数据，略过不翻译了。

4 结论

前面内容的总结，略过不翻译了。

单词、短语：

1.solved analytically 有解析解

2.a time-consuming numerical QP optimization 耗时的QP数值优化

3.numerical quadratic programming 数值二次规划，用数值优化的方法解QP问题

4.analytic QP 解析二次规划，用二次规划的解析解来解QP问题

5.margin 间隔

6.margin failure 落在间隔内

7.box constraint 边界约束

8.neural network non-linearities 非线性神经网络

9.a quadratic program 二次规划

10.chunking 分组

11.for some value of M 某些M值

12.zero Lagrange multipliers 零乘数，值为0的拉格朗日乘数

13.numerical QP optimization step QP数值优化步

14.self-consistent 自洽

15.uses a hierarchy of second choice heuristics 选择第二个乘数时有层次地使用启发式方法

16.make positive progress 取得优化效果

17.valid 有效

18.project the current primal point onto each constraint 投射当前初始点到每一个约束条件上

19.

minimizing the norm of the weight vector 最小化权重向量的取值范围，norm作“正常水平”解。本句主干为the primal problem of minimizing xx over xx space of (xx with xx) produces ...