晶体结构5——倒格子 布里渊区

倒格子(Reciprocal lattice)

二维晶体及其倒易点阵

在物理学中，倒易点阵是另一个点阵（通常是布拉维点阵）的傅立叶变换。在一般应用中，该第一晶格（其变换由倒格子表示）通常是实空间中的周期性空间函数，并且也被称为定向晶格。正格子存在于实际空间中并且是人们通常理解的物理晶格，倒格子存在于倒易空间（也称为动量空间或不常见的K空间，这是由于动量和位置是对偶关系）。因此，倒格子的倒格子是原来的正格子，因为两种晶格互为傅里叶变换。

倒易点阵在周期结构的大多数分析研究中起着基本性的作用，特别是在衍射理论中。在中子衍射和X射线衍射中，根据Laue条件，晶体的入射X射线和衍射X射线之间的动量差是倒格矢（ reciprocal lattice vector ）。晶体的衍射图案可以用于确定晶格的倒格矢。依此，可以推断晶体的原子排列。

数学描述

假定一个理想的布拉菲格子{\displaystyle \mathbf {R} _{\mathbf {n} }={n_{1}}\cdot \mathbf {a} _{1}+{n_{2}}\cdot \mathbf {a} _{2}} .其中 {\displaystyle n_{1},n_{2}\in \mathbb {Z} }

任何一个量(比如势能函数)，或者原子晶体中的电子密度可以写为周期函数

{\displaystyle f(\mathbf {r} )=f(\mathbf {R} _{\mathbf {n} }+\mathbf {r} )}

具有的周期性特点，在傅里叶展开中是非常有用的。

{\displaystyle f(\mathbf {R} _{\mathbf {n} }+\mathbf {r} )=\sum _{\mathbf {m} }{f_{\mathbf {m} }e^{i\mathbf {G} _{\mathbf {m} }\cdot {\mathbf {r} }}e^{i\mathbf {G} _{\mathbf {m} }\cdot {\mathbf {R_{n}} }}}}

因为对于任意的 {\displaystyle \mathbf {n} ,\mathbf {k} \in \mathbb {Z} ^{3}} ，有 {\displaystyle f(\mathbf {R} _{\mathbf {n} }+\mathbf {r} )=f(\mathbf {R} _{\mathbf {k} }+\mathbf {r} )}

那么最后一个式子对于特定情况 {\displaystyle \mathbf {R} _{\mathbf {0} }=\mathbf {0} }是正确的

{\displaystyle \sum _{\mathbf {m} }{f_{\mathbf {m} }e^{i\mathbf {G} _{\mathbf {m} }\cdot {\mathbf {r} }}e^{i\mathbf {G} _{\mathbf {m} }\cdot {\mathbf {R_{n}} }}}=\sum _{\mathbf {m} }{f_{\mathbf {m} }e^{i\mathbf {G} _{\mathbf {m} }\cdot {\mathbf {r} }}e^{i\mathbf {G} _{\mathbf {m} }\cdot {\mathbf {0} }}}=\sum _{\mathbf {m} }{f_{\mathbf {m} }e^{i\mathbf {G} _{\mathbf {m} }\cdot {\mathbf {r} }}1}}

所以一定得有

{\displaystyle e^{i\mathbf {G} _{\mathbf {m} }\cdot {\mathbf {R_{n}} }}=1}

这就意味着

{\displaystyle \mathbf {G} _{\mathbf {m} }\cdot {\mathbf {R_{n}} }=2\pi N} 其中 {\displaystyle N\in \mathbb {Z} }.

数学上，我们可以将倒格子描述为所有向量的集合 {\displaystyle \mathbf {G} _{\mathbf {m} }}

对于所有格点位置矢量R，其满足上述的一致性.

倒格子本身也是一个布拉维点阵，倒格子的倒格子就是原始晶格。

对于由它的原始向量定义的无限二维网格{\displaystyle (\mathbf {a_{1}} ,\mathbf {a_{2}} )}, 其倒格子可以通过它的两个倒易初始矢量生成，由下式来确定，

{\displaystyle \mathbf {G} _{\mathbf {m} }={m_{1}}\cdot \mathbf {b} _{1}+{m_{2}}\cdot \mathbf {b} _{2}}

其中,

{\displaystyle {\begin{aligned}\mathbf {b_{1}} &=2\pi {\frac {-\mathbf {R} \,\mathbf {a_{2}} }{-\mathbf {a_{1}} \cdot \mathbf {R} \,\mathbf {a_{2}} }}\\\mathbf {b_{2}} &=2\pi {\frac {\mathbf {R} \,\mathbf {a_{1}} }{\mathbf {a_{2}} \cdot \mathbf {R} \,\mathbf {a_{1}} }}\end{aligned}}}

这里 {\displaystyle \mathbf {R} } 表示一个90度的旋转矩阵(Rotate Matrix)

对于一个无限的三维网格, 由它的初始向量{\displaystyle (\mathbf {a_{1}} ,\mathbf {a_{2}} ,\mathbf {a_{3}} )}定义 , 它的倒格子由它的三个倒易初始向量决定, 由下式

{\displaystyle \mathbf {G} _{\mathbf {m} }={m_{1}}\cdot \mathbf {b} _{1}+{m_{2}}\cdot \mathbf {b} _{2}+{m_{3}}\cdot \mathbf {b} _{3}}

其中

{\displaystyle {\begin{aligned}\mathbf {b_{1}} &=2\pi {\frac {\mathbf {a_{2}} \times \mathbf {a_{3}} }{\mathbf {a_{1}} \cdot (\mathbf {a_{2}} \times \mathbf {a_{3}} )}}\\\mathbf {b_{2}} &=2\pi {\frac {\mathbf {a_{3}} \times \mathbf {a_{1}} }{\mathbf {a_{2}} \cdot (\mathbf {a_{3}} \times \mathbf {a_{1}} )}}\\\mathbf {b_{3}} &=2\pi {\frac {\mathbf {a_{1}} \times \mathbf {a_{2}} }{\mathbf {a_{3}} \cdot (\mathbf {a_{1}} \times \mathbf {a_{2}} )}}\end{aligned}}}

注意，分母是矢量的混合积。 使用（倒易）初始向量的列向量表示，上述公式可以使用矩阵求逆重写：

{\displaystyle \left[\mathbf {b_{1}} \mathbf {b_{2}} \mathbf {b_{3}} \right]^{T}=(2\pi )\left[\mathbf {a_{1}} \mathbf {a_{2}} \mathbf {a_{3}} \right]^{-1}.}

这种方式的定义，允许任意维度的概括。

上面的定义被称为“物理”定义，{\displaystyle 2\pi } 作为因子来自周期性结构的特点。“晶体学家”的等效定义，源于倒格子的定义 {\displaystyle e^{2\pi i\mathbf {K} \cdot \mathbf {R} }=1}, 其将倒格矢的定义改为:

{\displaystyle \mathbf {b_{1}} ={\frac {\mathbf {a_{2}} \times \mathbf {a_{3}} }{\mathbf {a_{1}} \cdot (\mathbf {a_{2}} \times \mathbf {a_{3}} )}}}等等其他向量。

晶体学家的定义的优点在于 {\displaystyle \mathbf {b_{1}} } 的定义仅仅是 {\displaystyle \mathbf {a_{1}} }的倒数，方向为{\displaystyle \mathbf {a_{2}} \times \mathbf {a_{3}} }，再除以因子{\displaystyle 2\pi }。 这可以简化某些数学操作，并且以空间频率为单位表示倒易晶格维度。

倒易点阵中的每个点（hkl）对应于实空间点阵中的一组点阵平面（hkl）。 倒格矢的方向对应于实空间平面的法线。 倒格矢的大小以长度的倒数给出，并等于实空间平面的晶面间距的倒数。

倒格子的性质

由倒易点阵的基矢定义，可得出倒格子的一些基本性质．

1. {\displaystyle \mathbf {b_{i}} \cdot \mathbf {a_{j}} =2\pi \delta _{ij}}

同时正格矢{\displaystyle \mathbf {R} _{\mathbf {n} }={n_{1}}\cdot \mathbf {a} _{1}+{n_{2}}\cdot \mathbf {a} _{2}}+n_3\cdot \mathbf {a} _{3}. 与倒格矢 {\displaystyle \mathbf {G} _{\mathbf {m} }={m_{1}}\cdot \mathbf {b} _{1}+{m_{2}}\cdot \mathbf {b} _{2}+{m_{3}}\cdot \mathbf {b} _{3}}的点积是2π的整数倍, 其中μ为整数．

正格子空间是实空间，或称位置空间、坐标空间，正格子空间中的矢量是位置矢量，可以表示为{\displaystyle \mathbf {r}=x\cdot \mathbf {a} _{1}+y\cdot \mathbf {a} _{2}}+z\cdot \mathbf {a} _{3}；倒格子空间是状态空间，倒格子空间中的矢量是波矢，可以表示为{\displaystyle \mathbf {q}=q_1\cdot \mathbf {b} _{1}+q_2\cdot \mathbf {b} _{2}}+q_3\cdot \mathbf {b} _{3}。

以 \vec{a}为基矢的格子，和以\vec{b}为基矢的格子，互为正、倒格子。

2、倒格子原胞体积Ω*与正格子原胞体积Ω之间有

\Omega^*=\vec{b_{1}}\cdot (\vec{b_{2}}\times \vec{b_{3}})=\frac{(2\pi)^3}{\Omega}
3. 倒格矢 \vec{G} _{{h_1h_2h_3} }垂直于正格子空间的晶面（h_1h_2h_3）

4. 面间距公式

正格子与倒格子的比较

各种晶体的倒格子

简立方晶格(Simple cubic lattice)

简立方布拉维点阵，边长为{\displaystyle a}的立方体原胞，对于简立方晶格的倒易点阵，其为边长是 {\displaystyle {\begin{matrix}{\frac {2\pi }{a}}\end{matrix}}}的立方体. 因此，立方晶格被称为自对偶，在倒易空间中具有与实空间中相同的对称性。

面心立方晶格（Face-centered cubic (FCC) lattice）

面心立方晶格的倒格子是体心立方

考虑FCC复式晶胞。 找到FCC的初级单胞，即具有一个格点的单胞。 现在将初级单胞的一个顶点作为原点。 给出真实晶格的基本向量。 然后从已知的公式，你可以计算倒易格子的基向量。 FCC的这些互逆晶格向量表示BCC实际晶格的基本向量。 注意，实际BCC晶格的基向量和FCC的互逆晶格在方向上彼此类似，但在幅度上不相似。

体心立方晶格（Body-centered cubic (BCC) lattice）

体心立方晶格的倒格子是面心立方

很容易证明 布拉菲格子 之间是90度 {\displaystyle (\mathbf {a_{1}} ,\mathbf {a_{2}} ,\mathbf {a_{3}} )} (立方, 四角, 正交)， {\displaystyle (\mathbf {b_{1}} ,\mathbf {b_{2}} ,\mathbf {b_{3}} )} 与它们的正空间矢量平行.

简单六角格子(Simple hexagonal lattice)

具有晶格常数为c和a的简单六方布拉维晶格的倒格子是具有晶格常数为 {\displaystyle {\begin{matrix}{\frac {2\pi }{c}}\end{matrix}}} 和{\displaystyle {\begin{matrix}{\frac {4\pi }{a{\sqrt {3}}}}\end{matrix}}}的另一个简单六角晶格，相对于正格子关于c轴旋转 30° . 因此，简单六角格子被称为自对偶，在倒易空间中具有与实空间中相同的对称性。

证明倒格子的倒易晶格是正格子

从它的定义，我们知道布拉维点阵的矢量必须在矢量加法和减法下闭合。 因此，如果我们有下式就足够了

{\displaystyle e^{i\mathbf {G_{1}} \cdot \mathbf {R} }=1}

以及

{\displaystyle e^{i\mathbf {G_{2}} \cdot \mathbf {R} }=1}

和与差{\displaystyle \mathbf {G_{1}} \pm \mathbf {G_{2}} }同样满足.

{\displaystyle {\begin{aligned}e^{i\mathbf {(G_{1}+G_{2})} \cdot \mathbf {R} }&=e^{i\mathbf {G_{1}} \cdot \mathbf {R} }\cdot e^{i\mathbf {G_{2}} \cdot \mathbf {R} }=1\cdot 1=1\\e^{i\mathbf {(G_{1}-G_{2})} \cdot \mathbf {R} }&=e^{i\mathbf {G_{1}} \cdot \mathbf {R} }/e^{i\mathbf {G_{2}} \cdot \mathbf {R} }=1\end{aligned}}}

因此，我们已经给出了在矢量加法和减法下闭合的倒易点阵。此外，我们知道一个倒格子矢量G可以表示为初始向量的线性组合.

{\displaystyle \mathbf {G} =k_{1}\mathbf {b_{1}} +k_{2}\mathbf {b_{2}} +k_{3}\mathbf {b_{3}} }

从前面的{\displaystyle \mathbf {b_{1}} }的定义, 我们可以得到:

{\displaystyle \mathbf {b_{i}} \cdot \mathbf {a_{j}} =2\pi \delta _{ij}}

其中 {\displaystyle \delta _{ij}}是克罗内克δ函数. R是正格子中的向量，我们可以将其表示为它的初始向量的线性组合。

{\displaystyle \mathbf {R} =n_{1}\mathbf {a_{1}} +n_{2}\mathbf {a_{2}} +n_{3}\mathbf {a_{3}} }

从这里我们可以得到:

{\displaystyle \mathbf {G} \cdot \mathbf {R} =2\pi (k_{1}n_{1}+k_{2}n_{2}+k_{3}n_{3})}

从倒格子的定义可知 {\displaystyle \mathbf {G} }必须满足下式.

{\displaystyle e^{i\mathbf {G} \cdot \mathbf {R} }=1}

为了满足这一点，我们必须有 {\displaystyle \mathbf {G} \cdot \mathbf {R} }等于{\displaystyle 2\pi }的整数倍.{\displaystyle n_{i}\in \mathbb {Z} } 、{\displaystyle k_{i}\in \mathbb {Z} }. 因此,倒格子也是布拉菲格子. 此外, 如果矢量{\displaystyle \mathbf {G} }构成倒易点阵 , 很显然对于任意的 {\displaystyle \mathbf {K} } 满足方程:

{\displaystyle e^{i\mathbf {K} \cdot \mathbf {G} }=1}

是倒格子的倒格矢. 根据{\displaystyle \mathbf {G} }的定义, 当 {\displaystyle \mathbf {K} } 是正格矢 {\displaystyle \mathbf {R} }, 我们有同样的关系式.

{\displaystyle e^{i\mathbf {R} \cdot \mathbf {G} }=1}

因此，我们可以得出结论：倒格子的倒格子是原始的正格子。

倒易空间

倒易空间（也称为“k空间”）是指空间函数的傅立叶变换的空间（类似地，频域是表示时间相关函数的傅立叶变换的空间）。 傅立叶变换使我们从“真实空间”到倒易空间，反之亦然。 相对空间在波力学中发挥作用：由于平面波可以写为具有波矢量k和角频率w的振荡项exp（i（kx-wt）），因此它可以看作是k和x的函数（以及w和t的函数）。 在空间中，是以kx = 2 * pi的周期振荡，因此对于给定的相位，k和x彼此互逆：k = 2 * pi / x和x = 2 * pi / k。

倒易点阵是该空间中的周期性点集，并且包含组成周期性空间晶格的傅里叶变换的 {\displaystyle {\vec {k}}} 点。 布里渊区是该空间内的体积，其包含代表在周期性结构中允许的经典或量子波的周期性的所有独特的k向量。

布里渊区（Brillouin zone）

在倒格子空间中以原点为中心的部分区域．

从倒格子空间原点，作与最近邻倒格点、次近邻倒格点、再次近邻倒格点、……的连线，再画出这些连线的垂直平分面。

包含原点的多面体所围区域就是第一布里渊区,与第一布里渊区相邻、且与第一布里渊区体积相等的区域为第二布里渊区;

与第二布里渊区相邻、且与第一布里渊区体积相等的区域为第三布里渊区;…．

第一布里渊区又称为简约布里渊区，简称布里渊区(Brillion Zone，记为BZ)，它是倒格子动量空间的Wigner-Seitz原胞．

1, 简立方正点阵的倒点阵，仍为简立方，故布里渊区形状仍是简立方.

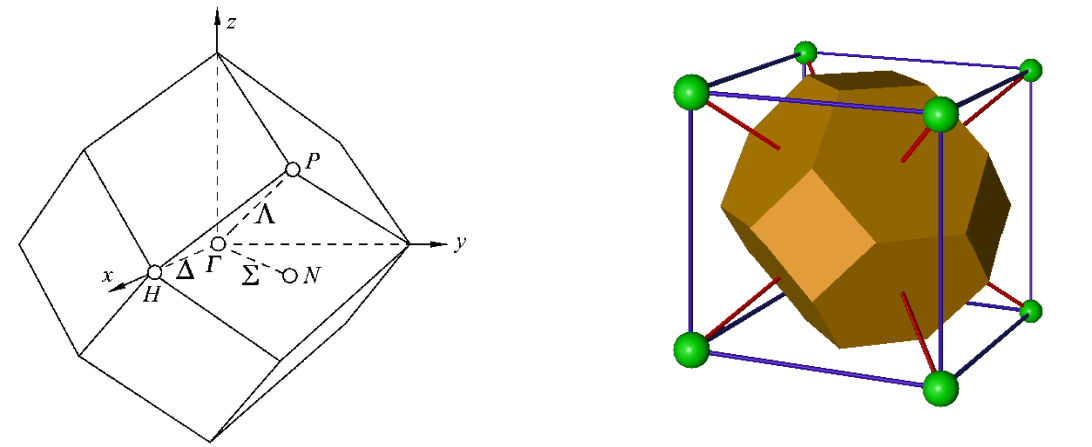
2, 体心立方正点阵的倒点阵，为面心立方，故布里渊区形状为菱形十二面体.

3，面心立方的倒点阵，为体心立方，故布里渊区形状是截角八面体（它是一个十四面体）．

倒格子的引入及其在晶体结构研究中的作用

以下内容引用自张天蓉老师的博文

是晶体衍射的示意图。根据布拉格衍射条件：2d sinθ = nλ，这儿，d是晶格常数，θ是衍射角。如果我们将波长λ用波矢量k=2p/l来代替的话，经过简单的代数变换后，很容易将衍射条件写成：

k sinθ= n(p/d) （1）

仔细观察下图（a），我们发现，不难从几何上理解公式（1）。它描述了满足衍射加强条件的波矢k与晶体结构中原子间距d之间的关系。满足衍射加强条件的波矢k的方向，也就是能打在衍射屏幕上而出现亮点的电磁波方向。所以，换言之，公式（1）描述了衍射图像亮点的位置与d之间的某种关系。什么样的关系呢？公式的右边是变量(p/d)的整数倍，这个变量与原子间距离d的倒数有关。

再进一步引伸下去，说得更清楚一些。图（a）所示的衍射实验，得到如（b）图所示的衍射图像，这个图像看起来是某种格点空间的映像。这个新格点空间不是晶格本身，但是又和原来的晶格有关系：新格点间的距离正比于原来晶格原子间距d的倒数。而且，新格子空间的量纲也倒过来了。原来的晶格是在真实空间中，点间的距离d是长度（米）的量纲，而新格点间的距离(p/d)的量纲是‘米’的倒数（1/米）。既然数值和量纲都是倒数的关系，人们便把这个虚拟的空间叫做 ‘倒格子’空间，见图（c）。
从数学的观点看，倒格子是原来周期性晶格的傅立叶变换【1】。说到傅立叶变换，大家比较熟悉的是从时间空间到频率空间的变换，时间的周期函数变换成频谱。比如，我们用光谱来研究光线中包含的各种颜色，用乐谱来表示音乐。对晶体来说，傅立叶变换将通常的坐标空间变换成了波矢空间。而原来坐标空间中的晶格，则变换成了波矢空间中的‘倒格子’。无论是正格子，还是倒格子，都属于我们在前一节中提到过的‘布拉菲点阵’。并且，正格子和倒格子在对称性方面互相关联，产生许多有趣的特性，在此不再赘述，读者可参考有关文献【2】。

现在，我们知道晶体的衍射图像对应于倒格子，就更加明白了布拉格父子工作的重要意义。因为固体中原子的晶格结构，是很难用显微镜直接观察到的。但是，X射线的衍射图像却已经可以得到。从X射线的衍射图像，我们可以计算出倒空间的几何结构，然后，再从倒空间，反过来又能计算出正晶格的相关常数，这样，晶体的结构不就一目了然了吗。因此，波矢空间及倒格子的概念，对研究固体物理的意义非常重大。探测晶体结构，不仅使用X-射线，也能用电子或中子衍射，从量子力学的观点，这些粒子（或电磁波）都具有波粒二象性，波矢反映了波动性，粒子性则可用动量表示。波矢与动量之间只相差一个常数因子，因此，波矢空间有时也称为动量空间。


【1】B. E. Warren (1969/1990) X-raydiffraction (Addison-Wesley, Reading MA/Dover, Mineola NY).
【2】《固体物理学》，黄昆、韩汝琦著，高等教育出版社出版，2005，

上一篇：