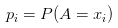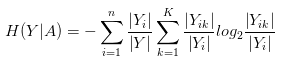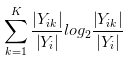数学 · 决策树(二)· 信息增益

射命丸咲

一个啥都想学的浮莲子
从直观来说,所谓信息增益,就是反映数据 A 能够给我们带来多少信息的一个度量。为了介绍信息增益,我们需要先弄明白什么是条件熵 H(Y | A)
- 它是基于熵定义的。需要注意的是,此时我们要关心的就不仅仅是“因变量” Y,也要关心“自变量” A。我们的最终目的,是根据 A 来判断 Y,这就有了条件熵的概念
- 先说直观理解:所谓条件熵,就是根据 A 的不同取值把 Y 分成好几份,对这些分开后的 Y 分别计算熵、再通过某种方式把这些熵合起来,得到总的条件熵。换句话说,就是将被 A 分开的各个部分的 Y 的混乱程度“加总”从而得到条件熵
- 所以,如果条件熵H(Y | A)越小,就意味着 Y 被 A 分开后的总的混乱程度越小、从而意味着 A 更能够帮助我们做出决策(感谢评论区 @小虫子 的提醒,这里之前的概念叙述和信息增益混淆了)
- 接下来就是数学定义:
定义完条件熵后,就可以来看信息增益了。由我上面说的直观理解,可能不少童鞋已经猜到了它的数学定义
对于具体的问题、比如决策树生成算法而言,我们需要使用经验熵来估计真正的熵:
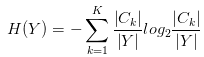
- \left| C_{k} \right| 、\left| Y \right| 表示第 k 类的个数和总样本数,从而\frac{\left| C_{k} \right|}{\left| Y \right|} 是p_{k}的估计(这里其实就是频率估计概率的思想。举个栗子,如果你去抽了一百次奖、也就是说\left| Y \right| = 100,用\left| C_{0} \right|表示你中奖次数的话,假设中了一次奖、也就是说\left| C_{0} \right| = 1,我们就估计这个抽奖)
- n 是 A 的取值的个数,根据 A 的这 n 个取值可以将 Y 分成 n 份。把Y_{i}当成Y,结合前面H(Y)的定义、可以得知定义中各个东西的数学内涵:
- Y_{i}就是Y的第 i 份,\left| Y_{ik} \right|代表着Y_{i}中第 k 类的个数
- \frac{\left| Y_{i} \right|}{\left| Y \right|}是p_{i}的估计,\frac{\left| Y_{ik} \right|}{\left| Y_{i} \right|}是p_{ik}的估计,思想同样是频率估计概率
- 所谓的
- 那么H(Y_{i})前面的系数\frac{\left| Y_{i} \right|}{\left| Y \right|}是什么呢?它代表着Y_{i}这一份样本的重要程度。\left| Y_{i} \right|越大、也就是说Y_{i}中样本越多,意味着Y_{i}的混乱程度、也就是说H(Y_{i})越应该得到重视
但如果简单地以g(Y, A)作为决策树的生成算法(也就是 ID3 算法)的话、会存在偏向于选择取值较多、也就是 n 比较大的特征的问题。我们可以从直观上去理解为什么这是个问题:
- 我们希望得到的决策树应该是比较深(又不会太深)的决策树,从而它可以基于多个方面而不是片面地根据某些特征来判断
- 如果单纯以g(Y, A)作为标准,由于g(Y, A)的直观意义是 Y 被 A 划分后混乱程度的减少量,可想而知,当 A 的取值很多时,Y 会被 A 划分成很多份、从而其混乱程度自然会减少很多、从而 ID3 算法会倾向于选择 A 作为划分依据。但如果这样做的话、可以想象、我们最终得到的决策树将会是一颗很胖很矮的决策树(……)、这并不是我们想要的
为解决这个问题,我们需要给 n 一个惩罚,信息增益比的概念因而诞生了(对应于 C4.5 算法):
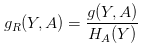
其中H_{A}{(Y)}是 Y 关于 A 的熵,它的定义为:

由熵的内涵我们可以得知,H_{A}Y总体上而言会随 n 的增大而增大
以上,我们大概讲了一下信息增益相关的数学知识,它对应的是决策树中的生成算法。我们会在下一章介绍一下决策树剪枝算法一些相关的数学定义
希望观众老爷们能够喜欢~
编辑于 2017-01-08 20:29