球面上的均匀分布：采样与格点

Machine Forgetting.

在知乎上写的第一篇文章。

几个月前就打算写一些关于目前学习和研究内容的笔记，但迟迟没有动笔。几天前@王赟 Maigo 在专栏文章10560 怎样在球面上「均匀」排列许多点？（上）及 10561 怎样在球面上「均匀」排列许多点？（下）中介绍了「斐波那契网格」，并从连分数和螺旋模式的角度分析了为什么这一类网格取黄金分割时具有良好的性质。鉴于最近毕业论文在做相关的内容，我想以此为第一篇，从概率论的角度探讨一下这个问题。

这篇文章将①简要介绍黎曼流形上的概率定义，介绍如何在流形上对均匀分布采样，以圆环、圆面、球面、球体为例给出实验结果；②简要分析「斐波那契格点」与均匀分布的关系，给出另外两类格点「正方形格点」与「六边形格点」的实验结果，指出思考的方向但理论分析留给后续工作。

写作经验不足，若有错漏请多指正。

一、黎曼流形上的概率定义

我们所熟知的随机变量、概率分布通常是定义在实数或n维欧几里得空间上的。其向量空间的性质使定义在其上的概率具有许多良好的特性且更容易分析。但在许多领域中，我们发现需要分析的数据很可能并不来自于某个欧式空间，例如图像、语音数据，数据的内禀维度远小于所处空间的维度，其标量乘或线性插值的结果没有意义；或者，已知的空间本身就不是欧式空间，例如地球地理信息是定义在球面上的，三维实向量的随机变量无法刻画其概率性质。这些事实迫使我们拓展概率的定义到更一般的空间上。

熟悉基于测度论的概率定义的读者知道，我们仅要求随机变量的取值空间是可测的；而对于熟悉流形的读者来说，光滑流形上的黎曼度量可以自然诱导出测度。这使得将概率定义在黎曼流形上是非常自然的。（由于篇幅所限这里略去细节，如果写完论文有时间的话再详细介绍）

用非常不严谨的话来说，像圆环、球体这一类局部“非常像”（微分同胚）一个欧式空间的几何对象（光滑流形）来说，若我们能知道每个点向两个“邻近方向”（切空间）的“夹角”（黎曼度量），我们就能知道它上面“一小块区域”（σ-代数子集）的“面积或体积”（测度），从而在它上面定义概率。

此外，像球面这样同时是一个群（SO(3)）和光滑流形的Lie群有一个很好的性质，由于对称性，我们仅需要单位元与欧式空间的映射(principal chart)就能比较不同的切空间。

对于最简单的情况均匀分布来说，概率密度函数定义为 p(x)=\frac{\mathbf{1}(x)}{\int_{\mathcal{M}}d\mathcal{M}}，其中1(x)为示性函数，分母是对黎曼流形全区域的积分。

这样，我们就有了讨论球面上的均匀分布的基础。

二、均匀分布与采样

仅有黎曼流形上的概率定义并不能实际地描述一种分布或可计算地从某个分布中取样。我们需要一个坐标。我们知道，在不同坐标下积分时的积分变换相差一个雅克比行列式。

在\mathbb{R}^2的情况，我们可以通过极坐标容易地描述一个圆盘。和直角坐标的变换为\begin{split} x&=r\cos(\theta)\\ y&=r\sin(\theta) \end{split}时，其雅克比行列式为J = \det\frac{\partial (x,y)}{\partial (r,\phi)}=r，则面积元为dA=dxdy= r\,drd\theta=d(\frac12r^2)d\theta。

类似x与y服从独立的均匀分布时我们可以得到矩形上的均匀分布，

当r \sim \sqrt{Uniform(0,R^2)},\, \theta \sim Uniform(0,2\pi)时，我们可以得到圆盘上的均匀分布。

对于三维的球面、球体也是一样，有

球坐标

\begin{split} x&=r\cos\theta\sin\phi\\ y&=r\sin\theta\sin\phi\\ z&=r\cos\phi \end{split}，体积元为dV= r^2\sin\theta\,dr d\theta d\phi= d(\frac13r^3)d(-\cos\theta)d\phi
柱坐标

\begin{split} x&=\rho\cos\phi\\ y&=\rho\sin\phi\\ z&=z \end{split}，体积元为dV=\rho \, d\rho d\phi dz = d(\frac12\rho^2) d\phi dz

Sphere Point Picking 中给出了具体公式，这解释了公式中的arccos、二次方根、三次方根。细节略去。

下图是从圆环、圆面、球面、球体上的均匀分布中采样得到的结果：

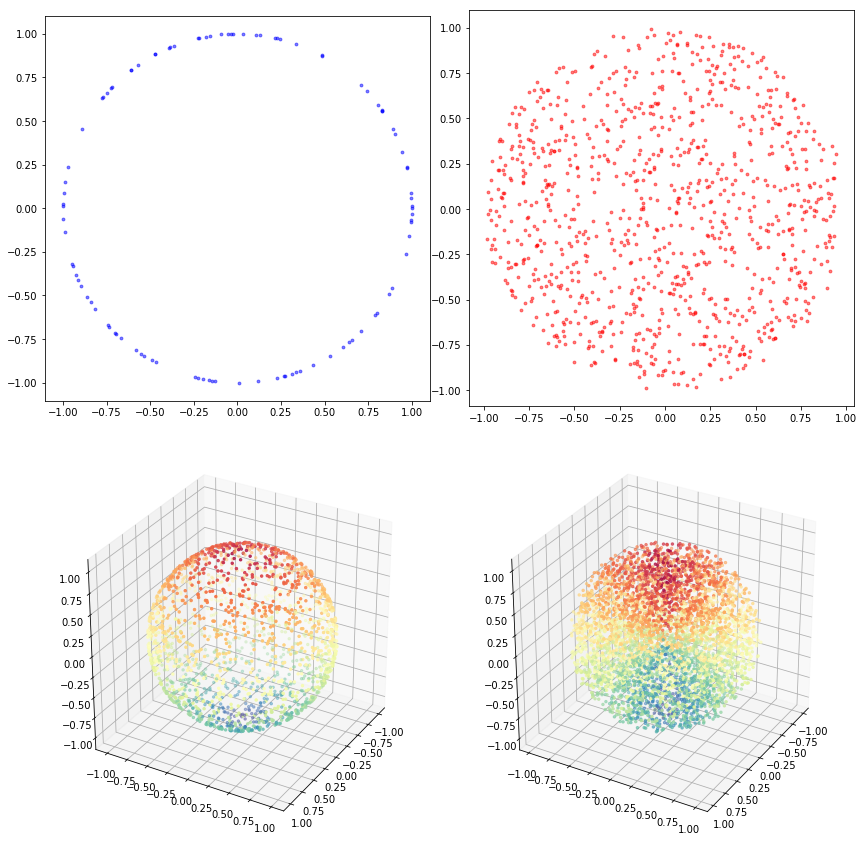
我们可以考虑极坐标下的圆盘（欧式空间）与柱坐标下的球面（黎曼流形）间的映射，联系两者的均匀分布。出于这一点，为了使可视化更清晰，下一节我们考虑用格点近似圆盘上的均匀分布的问题。

三、单参数格点近似

注意，参数满足r \sim \sqrt{Uniform(0,R^2)},\, \theta \sim Uniform(0,2\pi)时可得圆盘上的均匀分布。即\theta-r^2空间中是二维矩形上的均匀分布。若我们以某种确定性的格点代替均匀分布的采样，映射后我们能得到「近似均匀」的格点。所以我们希望格点的边际分布近似是均匀分布。

1. 斐波那契格点

首先我们考虑以实数k为参数、以自然数n（相当于0到R^2上等间距的点）参数化的一类格点：
\begin{split} \theta&=2\pi kn\equiv (2\pi kn)\mod 2\pi =2\pi \{kn\}\\ r^2&=n \end{split}，其中{kn}表示kn的小数部分。

r^2等间距取点是均匀分布的最佳近似（其实这也是一个可以展开的话题，想一想为什么，怎么证明？），但θ上的{kn}并不一定是均匀分布的。不同k时 {kn}的「均匀性」是映射后格点是否均匀的关键。事实上，黄金分割\phi=\frac{\sqrt5-1}{2}\approx 0.618034具有使{kn}“非常均匀”的性质。

我们可以将参数空间及“边际分布”绘出：

可以看出k = ϕ时θ是非常接近均匀分布的。

这涉及了一个称作等分布数列的概念：一个数列x_n被称为区间[a,b]上的等分布数列，则在任何子区间中找到其元素的概率正比于区间长度，即近似均匀分布的采样。x_n=\{\phi n\}是一个在(0,1)上的等分布数列，满足这样的性质的k值有\phi=\frac{\sqrt5-1}{2}，\sqrt2+1，e等。圆周率\pi并不满足这个性质。

下图绘出了k取不同值时{kn}前1000个数取值的直方图：