光学系统像差杂谈（1）：费马原理

光学话题下的优秀答主

这个系列是我一直以来想要写的，然而迟迟未动笔，实在是担心实力不够，写出来不伦不类。最近跟人聊天，聊到相机镜头的表现，不免又谈论起像差的话题，发现即使是相当资深的发烧友也对很多概念理解有误。借着这个契机心里又燃起了下笔的热情，趁热打铁，先写下来再说了。本来也是想写成一些随笔或者笔记的形式，所以章节之间的逻辑性就顾不上了，大体上就是我想到哪儿写到哪儿，还望读到文章的朋友们海涵。

1 费马原理

作为开篇的第一节，直接把费马原理拿过来讲，似乎迈的步子有点大。然而在现代物理的概念中，物理学家们更偏爱从基础的守恒律出发作为基石来构建上层建筑，所谓第一性原理，比如从动量守恒律出发，推导出牛顿定律。而在经典几何光学里，费马原理就是这样一种基础性的原理。直接从费马原理出发，可以帮助建立更宏观的印象。

费马原理说的是什么呢？维基百科词条 Fermat's principle 里是这么说的：

A more modern statement of the principle is that rays of light traverse the path of stationary optical length with respect to variations of the path.

我自己这么翻译：

光走的路径，是光程稳定的路径。

这里先不多做饶舌的解释，大体理解成光走的路径，是所有可能路径里用时最短、或者最长、或者恒定的。

举个例子，均匀介质中，从 A 点到 B 点，光线可以走很多路径（如图中蓝色的路径），然而光线实际走的路径是红色的那条，根据简单的几何学知识我们知道，两点之间线段最短，也就是说那条路径是所有可能的路径中用时最短的。这里我们从费马原理推导出了「均匀介质中光沿直线传播」这一规律。

再举个例子，假设光线在两种不同介质中的速度是 v_1 和 v_2，从 A 点到 B 点中间经过 C 点折射。不妨设中间分界面为 y 轴，并且 A 点坐标为 (x_A,y_A)，B 点坐标为 (x_B,y_B)，C 点坐标为 (0,y)

光线走过 ACB 折线所需时间为

t = \frac{\sqrt{x_A^2 + (y_A - y)^2}}{v_1} + \frac{\sqrt{x_B^2 + (y_B - y)^2}}{v_2}

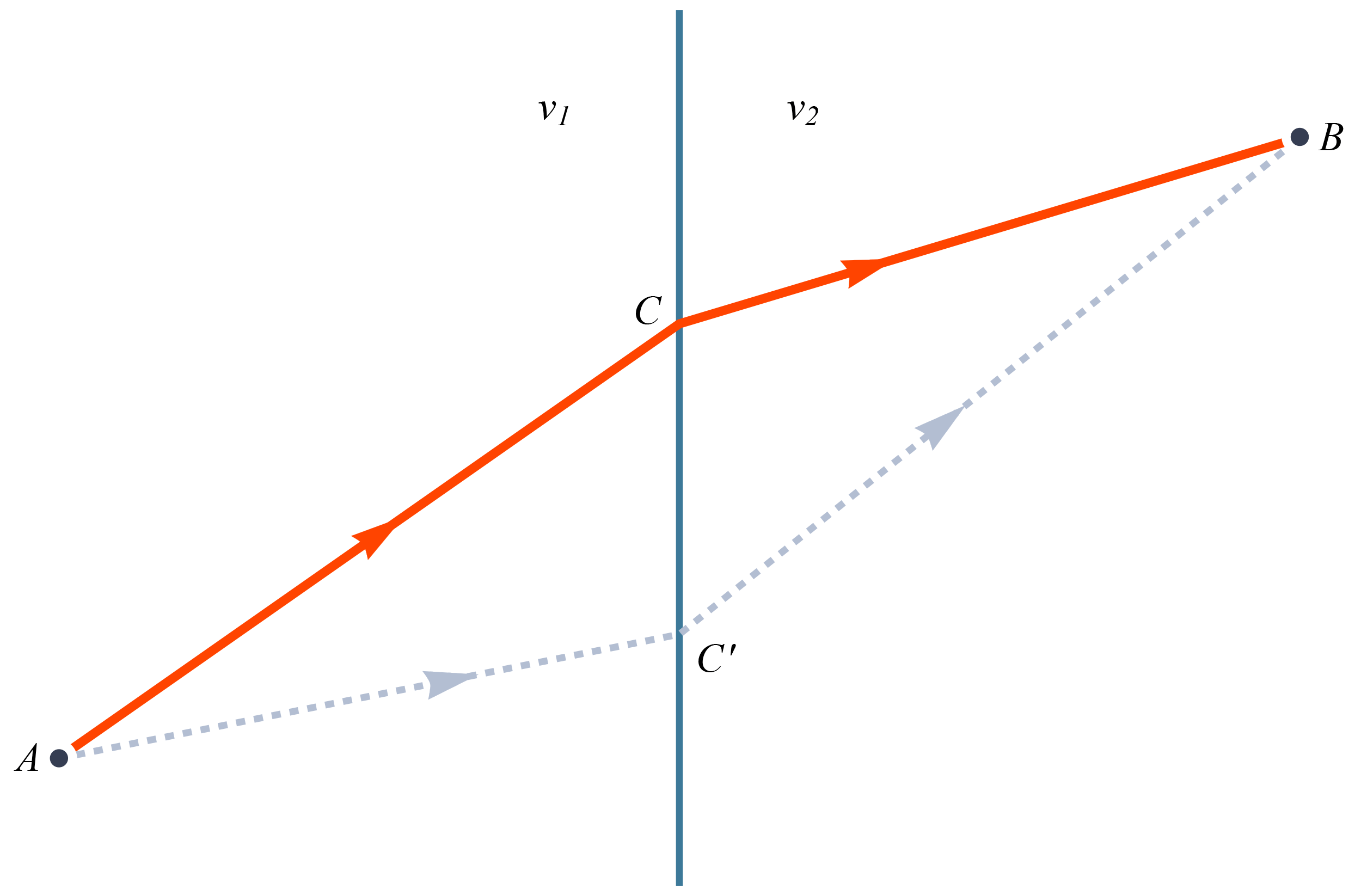
若要光程稳定，就是时间 t 对 C 的位置的微分为 0：

\frac{\text{d}t}{\text{d}y} = \frac{y-y_A}{v_1\sqrt{x_A^2 + (y_A - y)^2}} + \frac{y-y_B}{v_2\sqrt{x_B^2 + (y_B - y)^2}} = 0

注意到上式中 (y-y_A) / \sqrt{x_A^2 + (y_A - y)^2} 就是入射角的正弦值 \sin i，(y-y_B) / \sqrt{x_B^2 + (y_B - y)^2} 就是出射角的正弦值的相反数 -\sin i'，那么我们就直接得到了折射定律（Snell's Law）：

\frac{\sin i}{v_1} = \frac{\sin i'}{v_2}

2 等光程成像

对于一个光学系统来说，一个简单的场景就是对一个点光源成一个点像，如下图所示。

这里我们不深入细节，不关心这个光学系统是怎么造出来的，不关心里面有几个折射面有几个反射面，整个光学系统就看做一个黑箱，他的作用就是把一个点发出的光线，汇聚到另一个点。在这里，我们姑且把这种光学系统称作理想光学系统（当然，在之后的文章中会多次出现这个概念，会有更充分的说明）。我们看看，要做到这一步，这个光学系统应该满足什么条件。

我们还是运用费马原理来分析，这里用费马原理的好处就出来了，从一个更高更抽象的层面来看问题，可以不用管光学系统内部各种细节。对这样一个场景，如上图，光线从 A 点到 B 点，可以走任意一条红色的路径，而不是唯一的路径。这一点和前面分析的场景都不同了，之前分析的场景中，光线从一点到另一点，只有一条唯一的路径，而在这里表现为可以有无数条可行的路径。根据费马原理，这意味着这些路径都应该满足一个条件：等光程，换句话说，光沿着这些红色的路径走，所需要的时间都是相等的。

你看，我们完全没有关心光学系统的细节，就推导出了理想光学系统应该满足的成像条件，这就是用费马原理的方便之处。

更进一步的，我们有了等光程的概念，分析的对象也可以不再局限于具体的点光源。从一个点光源发出的光，经过相等的时间，都会到达一个球面，这个面就叫做「等光程面」，从波的角度看就是「波前（Wavefront）」。既然从点光源到这个球面的光程相等，那么我们分析的时候，就可以不用从实际点光源出发，而是从这个等光程面出发，来计算光程就可以了；并且，我们也不必计算到成像点的光程，而只要计算到距离成像点相等光程另一个等光程面就可以了。

有了等光程面（波前）的概念，我们可以进一步描述理想光学系统。显然，从点光源出发的等光程面是一个球面，距离成像点相等光程的等光程面也是一个球面。如果把平面波看做半径无穷大的球面，事实上这就把平行光（无穷远点）也一并包括进来了。所以理想光学系统就可以描述为：把球面波前转换为另一个球面波前。

3 实际应用：圆锥曲线的光学性质

我们来看几个等光程条件实际运用的例子。在中学的解析几何中，我们都学过圆锥曲线，也了解到圆锥曲线的光学性质，下面我们来运用等光程条件来分析一下圆锥曲线的光学性质。

我们先看椭圆，根据定义，椭圆上任意一点「到两焦点距离之和为定值」，也就是说，下图中所有红色的路径总长度都相等，F_1C+CF_2 等于一个定值；如果光沿着这些路径走，就是等光程的。所以实际中，如果其中一个焦点是一个点光源，那么经过椭圆的反射，就一定会在另一个焦点处成一个完美点像。

再看看抛物线，我们来计算一下平行光入射到焦点的光程。很显然，平行光的等光程面就是一个平面，我们就从这个平面出发进行光程计算。根据定义，抛物线上任意一点「到准线的距离等于到焦点的距离」，也就是说对抛物线上任意一点 B，都有 AB+BF=AB+BC=AC，这里容易看出 AC 的长度是一个定值，所以图中这些红色的路径都是等光程的，所以抛物线可以把平行光完美地汇聚到焦点上。