看明白Julia集
该作者非常努力，介绍都发表在了Nature
在复杂动力学里，Julia集是个著名的“混沌”行为的集（与之对应的是Fatou集，“非混沌”集）
主要表现是无法预测下一个点的位置，但是把所有点画完就可以出来一个非常好看的图
比如说Julia集的一个公式： - z = z^2 + c
其中z c都是复数，c是复数常量，z中的实数部和虚数部构成一个点，然后不同的迭代迭代，不发散的点构成的点集就称为Julia集（Julia发现的），这些点构成的图形就形成了一个Julia集的分形图。
当然大家都发现了公式右边是z的平方吧？如果我改下这个数字会怎么样呢？
（From Wikipedia）我们由此可以猜测，z的几次方就对应他有几个“角”。
他还有个特点就是“自相似”
Example :
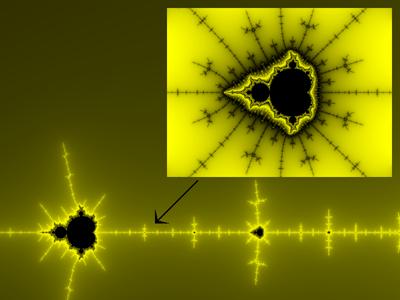
右上的和左下的是不是相似？
大概公式里面也能说明，因为他的下一个位置都是由他自己乘自己得到。
现在搞清楚了Julia集是咋回事，那么他的公式中的常量C有什么用呢？
常量C可厉害了
C = a + bi（a b取值范围都是-1 到 1）
我们先试验下，让a = 0（实数为0） b从-1 到 1 再回到 -1来看图像会怎么样
然后令b = 0（虚数为0）, a从-1 到 1 再回到-1 ，我们看看效果：
可以看出常量C的实数和虚数就是控制这图案的形状的量。
那么应该怎么画这个图形？
代码附上：
void drawJuliaSet(Graphics2D g) {
BufferedImage image = new BufferedImage(w, h,
BufferedImage.TYPE_INT_RGB);//w h为窗体宽度和高度
double zx, zy, cX, cY;//这里就是cX和cY
for (int x = 0; x < w; x++) {//套公式
for (int y = 0; y < h; y++) {
zx = 1.5 * (x - w / 2) / w;
zy = (y - h / 2) / w;
float i = 200;
while (zx * zx + zy * zy < 4 && i > 0) {
double tmp = zx * zx - zy * zy + cX;
zy = 2.0 * zx * zy + cY;
zx = tmp;
i--;
}//依据收敛性设置颜色
int c = Color.HSBtoRGB((200 / i) % 1, 1, i > 0 ? 1 : 0);
image.setRGB(x, y, c);
}
}
g.drawImage(image, 0, 0, null);
}要做出动画效果还是有点困难，因为每张图要花0.2s~0.4s，分辨率高了就更难受，所以我选择预先画200张，再把图片一次性画完。
上面都是源于公式： z=z^2+c
大家可以自己用手先试试，收敛的点放在一起就能组成这样的分形图，甚至，您都可以用控制台画出Julia集的分形图！
像这样：
哈哈哈，不敢相信吧，那么赶紧带上代码去旅行吧！
发布于 2017-08-08 15:54
