Perona-Malik方程(各向同性非线性扩散实现图像滤波)
1. Perona-Malik方程
之前所使用的线性扩散图像滤波会对整幅图像“一视同仁”,不管是边缘纹理还是其他结构都会等同于噪声一起滤除。这会使图像过于平滑而且丢失很多高频信息。如果我们使用非线性扩散的方法,即:传导系数会随着图像的局部特征改变而改变,例如在图像平滑区域传导系数自适应增大可以更好的滤除噪声,在图像的边缘纹理区域系数自适应减小可以更好的保存图像边缘。
首先,PM扩散方程为:它的来源是将梯度的模值信息融合到传输系数中,并带入公式(5)可得:
\begin{cases} \frac{\partial I(x,y,t)}{\partial t}&=\text{div}[g(|\nabla I|)\nabla I]\\ I(x,y,0)&=I_0(x,y) \end{cases}\tag{1}
其中 \nabla I 为梯度的模值: |\nabla I(x,y)|=(I_x^2+I_y^2)^{1/2} , g 为边缘函数,或者边缘停止函数。常用的边缘函数比如:
g(r)=\frac{1}{1+(r/K)^p},p=1,2\tag{2}
这里K是选定的常数,作用是控制g的下降速率。下图为p=1的条件下K=10, 20的下降曲线。
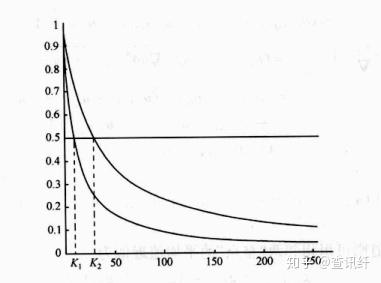
由于在图像的边缘中梯度的模值 |\nabla I| 取得极大值,而优化公式整体是求极小值的,为了避免在优化公式中引入负号,因此要引入一个单调递减而且是非负的边缘函数 g(\cdot) ,它可以保证在 |\nabla I| 取得极大值时, g(|\nabla I|) 取得局部极小值。它最早在图像分割和边缘检测问题中被提出,由于该函数的性质是可以将方程的解向着梯度变大的方向移动,最终停止在图像的边缘上,因此也被称为边缘停止函数。
2. P-M方程行为分析
首先将P-M方程简化为一维的情况分析:
\begin{aligned} I_t&=\frac{\partial}{\partial x}[g(|I_x|)I_x]=g'\frac{I_xI_{xx}}{\sqrt{I_x^2}}I_x+g(|I_x|)I_{xx} \\ &=[g'|I_x|+g(|I_x|)]I_{xx}=\phi'(|I_x|)I_{xx} \end{aligned}\tag{3}
其中 I 的下角标表示对某个变量求导。 \phi(r):=rg(r) 称之为影响函数。将(11)式中的g(-)函数带入可得:

下面是 \phi 的函数曲线图:

- 当p=1时, \phi' 从最大值1单调递减到0,而且始终保持正值,因此这种情况下的(12)式总保持正向扩散。
- 当p=2时, \begin{cases} \phi'\ge0,\quad 0\le r \le K\\ \phi'<0,\quad r>K \end{cases}\\ 这个不等式说明在梯度较小的图像平滑区域,即: |\nabla I|<K 时,导数大于0为正向扩散。在梯度较大的边缘纹理区域,导数小于0为反向扩散。反向扩散的含义是:杂质将从浓度低的地方流向浓度高的地方,这意味着图像边缘的锐化。
在后面二维P-M方程的分析中,可以得出结论:当选用合适的边缘函数g时,P-M方程可以自适应的实现图像去噪和边缘增强的效果。
3. P-M方程的病态性质
数学研究表示(1)式给出的初值的P-M方程极有可能是病态的。如果定义下面这个能量泛函:
E(I)=\int_\Omega \rho(|\nabla I|){\text{d}}\Omega\tag 4
其中 \rho(\cdot) 是一个非负函数而且在0处取得的值为0。那么依据变分原理,最小化该能量泛函对应的梯度下降流为:
\frac{\partial I}{\partial t}=\text{div}\left[\rho'(|\nabla I|)\frac{\nabla I}{|\nabla I|}\right]\tag 5
如果将 \frac{\rho'(|\nabla I|)}{|\nabla I|} 改写为: g(|\nabla I|) ,那么(5)式就和(1)式完全一致。也就是说P-M方程可以看做是(4)式能量泛函的梯度下降流。其边缘函数g由(4)式中的 \rho(\cdot) 函数决定。再与式(3)做比较可得函数的\rho(\cdot) 的导数就是前面所定义的 \color{red}{影响函数} :
\rho'(r)=\phi(r)\tag 6
4. P-M方程的正则化
一般来说,病态问题都是一个方程对应着多个解,因此需要用正则化的方法使它变成一个适定问题(well-posed)。有研究者提出一种新的改进方案为:
I_t=\text{div}\left[g(|\nabla I_\sigma|)\nabla I\right]\tag 7
其中
I_\sigma(x,y,t)=G_\sigma*I(x,y,t)\\
G_\sigma 表示方差为 \sigma 的Gaussian函数,(7)式称之为正则化的P-M方程,或者叫CLMC模型。
5.P-M方程求解代码
搬运自:
公式分析参考:
function diff_im = anisodiff2D(im, num_iter, delta_t, kappa, option)
%ANISODIFF2D 经典PM模型的各向异性扩散
% DIFF_IM = ANISODIFF2D(IM, NUM_ITER, DELTA_T, KAPPA, OPTION)
% 该函数执行灰度图像上的各向异性扩散(经典PM模型),被认为是一个二维的网络结构的8个相邻节点的扩散传导。
%
% 参数描述:
% IM - 灰度图 (MxN).
% NUM_ITER - 迭代次数
% DELTA_T - 积分常数 (0 <= delta_t <= 1/7).通常情况下,由于数值稳定性,此参数设置为它的最大值。
% KAPPA - 控制传导的梯度模阈值。控制平滑。
% OPTION - 传导系数函数选择(Perona & Malik提出):
% 1 - c(x,y,t) = exp(-(nablaI/kappa).^2),
% privileges high-contrast edges over low-contrast ones.
% 2 - c(x,y,t) = 1./(1 + (nablaI/kappa).^2),
% privileges wide regions over smaller ones.
%
% 输出描述:
% DIFF_IM - 具有最大尺度空间参数的(扩散)图像。
%
% 使用例子:
% -------------
% s = phantom(512) + randn(512);
% num_iter = 15;
% delta_t = 1/7;%越大越平滑
% kappa = 30;%越大越平滑
% option = 2;
% ad = anisodiff2D(s,num_iter,delta_t,kappa,option);
% figure, subplot 121, imshow(s,[]), subplot 122, imshow(ad,[]);
% 转换输入图像类型为double.
im = double(im);
% PDE(偏微分方程)的初始条件。
diff_im = im;
% 中心像素距离。
dx = 1;
dy = 1;
dd = sqrt(2);
% 二维卷积掩模-8个方向上的梯度差分。
hN = [0 1 0; 0 -1 0; 0 0 0];
hS = [0 0 0; 0 -1 0; 0 1 0];
hE = [0 0 0; 0 -1 1; 0 0 0];
hW = [0 0 0; 1 -1 0; 0 0 0];
hNE = [0 0 1; 0 -1 0; 0 0 0];
hSE = [0 0 0; 0 -1 0; 0 0 1];
hSW = [0 0 0; 0 -1 0; 1 0 0];
hNW = [1 0 0; 0 -1 0; 0 0 0];
% 各向异性扩散
for t = 1:num_iter
% 8个方向梯度差分. [imfilter(.,.,'conv') 也可以使用 conv2(.,.,'same')]
nablaN = imfilter(diff_im,hN,'conv');
nablaS = imfilter(diff_im,hS,'conv');
nablaW = imfilter(diff_im,hW,'conv');
nablaE = imfilter(diff_im,hE,'conv');
nablaNE = imfilter(diff_im,hNE,'conv');
nablaSE = imfilter(diff_im,hSE,'conv');
nablaSW = imfilter(diff_im,hSW,'conv');
nablaNW = imfilter(diff_im,hNW,'conv');
% 扩散函数
if option == 1
cN = exp(-(nablaN/kappa).^2);
cS = exp(-(nablaS/kappa).^2);
cW = exp(-(nablaW/kappa).^2);
cE = exp(-(nablaE/kappa).^2);
cNE = exp(-(nablaNE/kappa).^2);
cSE = exp(-(nablaSE/kappa).^2);
cSW = exp(-(nablaSW/kappa).^2);
cNW = exp(-(nablaNW/kappa).^2);
elseif option == 2
cN = 1./(1 + (nablaN/kappa).^2);
cS = 1./(1 + (nablaS/kappa).^2);
cW = 1./(1 + (nablaW/kappa).^2);
cE = 1./(1 + (nablaE/kappa).^2);
cNE = 1./(1 + (nablaNE/kappa).^2);
cSE = 1./(1 + (nablaSE/kappa).^2);
cSW = 1./(1 + (nablaSW/kappa).^2);
cNW = 1./(1 + (nablaNW/kappa).^2);
end
% 离散偏微分方程的解决方案
diff_im = diff_im + ...
delta_t*(...
(1/(dy^2))*cN.*nablaN + (1/(dy^2))*cS.*nablaS + ...
(1/(dx^2))*cW.*nablaW + (1/(dx^2))*cE.*nablaE + ...
(1/(dd^2))*cNE.*nablaNE + (1/(dd^2))*cSE.*nablaSE + ...
(1/(dd^2))*cSW.*nablaSW + (1/(dd^2))*cNW.*nablaNW );
% 迭代的警告
fprintf('\rIteration %d\n',t);
end
