KNN和K-mean有什么不同？

问题：KNN和K-means聚类有什么不同？ 在KNN或K-means中，我们是用欧氏距离来计算最近的邻居之间的距离，为什么不用曼哈顿距离？

回答：

首先我们比较一下Knn和K-means的基本算法原理。

KNN

• 分类算法
• 监督学习
• 数据集是带Label的数据
• 没有明显的训练过程，基于Memory-based learning
• K值含义 - 对于一个样本X，要给它分类，首先从数据集中，在X附近找离它最近的K个数据点，将它划分为归属于类别最多的一类

K-means

• 聚类算法
• 非监督学习
• 数据集是无Label，杂乱无章的数据
• 有明显的训练过程
• K值含义- K是事先设定的数字，将数据集分为K个簇，需要依靠人的先验知识

不同点：

两种算法之间的根本区别是，K-means本质上是无监督学习，而KNN是监督学习；K-means是聚类算法，KNN是分类（或回归）算法。

K-means算法把一个数据集分割成簇，使得形成的簇是同构的，每个簇里的点相互靠近。该算法试图维持这些簇之间有足够的可分离性。由于无监督的性质，这些簇没有任何标签。KNN算法尝试基于其k（可以是任何数目）个周围邻居来对未标记的观察进行分类。它也被称为懒惰学习法，因为它涉及最小的模型训练。因此，它不用训练数据对未看见的数据集进行泛化。

相似点：算法都包含给定一个点，在数据集中查找离它最近的点的过程。

关于为什么不用曼哈顿距离而是采用欧氏距离。主要是因为曼哈顿距离只计算水平和垂直距离，所以有维度的限制。欧氏距离可以用于任何空间距离的计算问题。由于数据点可能存在于任何空间，所以欧氏距离是更为可行的选择。

你或许会问，什么是欧氏距离，什么是曼哈顿距离呢？让我们来看一张图吧！

可以看到，曼哈顿距离（Manhattan Distance）就像曼哈顿的街道一样，只有水平和垂直的线段。欧氏距离（Euclidean Distance）则是可以量测任意方向的线段。我们看看他们的定义公式就一目了然：

欧式距离

曼哈顿距离

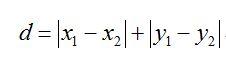
题图来源：Bing