Kaggle HousePrice : （前１５％）,（2.实践-特征工程部分-之上古魔法-统计检验）

王勇

目前感兴趣：数字化转型，过程挖掘，数据异常，R

关键词：回归评估，整体检验，显著性，多重共线性，奇异矩阵

ftest, ttest, significance level, R2, multi_col linearity,singular matrix

Kaggle, 统计，机器学习,python

预计阅读时间： ２0分钟，后１5分钟，假定读者已经拥有相关的统计检验背景知识。

本文目标：

通过比较，引入传统的统计方法（上古魔法），打开数据集的黑盒子。探讨如下方法：

检验训练集和测试集是否相同分布。相同分布，是统计方法和机器学习的共同前提。这可以帮助预判后面的机器学习的训练，调参和stacking是否有意义？
统计检验发现的概率(p value)帮助做feature selection辅助。
检查变量间是否存在共线性关系(奇异矩阵，不满秩) ? 后期机器学习，或者预处理，应该采用什么样的方式正则化处理? 例如：

直接用PCA降维。
是否需要采用Normalzier来正则化处理
Lasso(L1）还是Ridge(L2),
XGBoost，lightGBM应该怎么结合L1,L2

在知乎和Python中文社区发表了两篇经验分享文章，都是关于在Kaggle House Price的文章，着重讲的是如何用搭积木的方式，稳定的将成绩提高。已经发表了两篇篇文章如下：

Kaggle HousePrice : LB 0.11666（排名前１５％）, 用搭积木的方式（1.原理）

Kaggle HousePrice : LB 0.11666（前１５％）, 用搭积木的方式（2.实践-特征工程部分）

原计划在第二篇文章收集满100个赞后发表第三篇文章，即：训练，调参和Ensemble。尽管还没有100赞。但是收到了许多呼友关注。我在阅读呼友关注的其他文章时，也受到了挺多启发。其中最有意思的就是统计（上古魔法）ＶＳ机器学习（开上帝视角）vs的讨论。

知乎和一些书籍上都有对比统计方法和机器学习方法，非常精彩。品味这些文章和书籍后，我的理解是：

两者相同之处：　针对已有的数据，推导出来理解和认知。
两者不同之处：

统计方法就像上古魔法。　为啥：

数据很少，数据很宝贵，
计算能力也能昂贵。
主要靠神秘的魔法师和神秘的魔法，即统计学家，统计和概率学。

统计学家，开山鼻祖就是来自北方冰雪之国的Kolmogorov马尔可夫。

统计和概率的基础：假设，中心极限定理，大数定理等。

机器学习就像开了上帝视角的游戏玩家。为啥，通常：

数据又多又广（足够多的话，就好比开了上帝视角的游戏玩家）

训练数据可能有数百万条，甚至更多。例如：Kaggle 的Bosche 生产线优化案例，解压后数据文件超过了60G, 数据记录约5百万条（注：Dream competition 之一，可惜对机器内存，和算力要求太高。 Kaggle上的许多选手都只采用了部分数据抽样来作预测）
训练数据(sample)足够广，甚至可以作为总体(population)来看待。
上面这两点都成立的话，这简直就是游戏中的上帝视角。　所有尽在掌握了。

计算能力便宜。云计算和ＧＰＵ，ＴＰＵ让计算机时不再成为约束。

等等，扯了半天。这和Kaggle HousePrice 2.实践-特征工程部分文章有啥关系？　

为啥在浪费时间，浪费口水，扯上面的东西？

答案是，

在House Price 机器学习的优势并不显著呀！

首先，数据机不多也不广.　上帝视角没有开

训练集只有1460条记录，测试集和训练集几乎相等。上帝

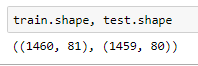
其次，计算能力也不够。　自费玩Ｋａｇｇｌｅ的限制。　文章第一篇，我说过参加比赛用的机器是阿里云－最低配版本（单核１Ｇｃｐｕ，１Ｇ内存）。ＧｒａｄｉｅｎｔＢｏｏｓｔ，这类算法耗时太长，基本就不用。甚至传说中的ＸＧＢｏｏｓｔ神器，也只是参考使用。在（ｎ＿ｅｓｔｉｍａｔｏｒ）小于３０００时，ＲＭＳＥ成绩太差。大于３０００后，计算单个Ｐｉｐｅ就要用上０．５到１个小时。　更不要说，Ｓｔａｃｋｉｎｇ　和Ｅｎｓｅｍｂｌｅ时候的ＣＶ叠加时间，Ｎ小时。Ｎ＞２。

那么，

为什么不用统计方法来看看？

说干就干。

应该是如下几个步骤：

１。检验训练集和测试集是否来自同一个分布？　　如果不是，就洗洗睡吧。　统计方法或者机器学习没有意义的。如果是同一个分布，不能拒绝学习时有意义的这一假设。

上面的话比较拗口，简单说来。就好比，拿乐高得宝积木来玩普通乐高积木。两者虽然都是积木，但是大小尺寸不一样。＂通常＂不能直接一起玩。

２．用统计方法，来看看（采用经典二乘法）下面这些情况。

　　回归的整体结果是否有意义（Ｆｔｅｓｔ）　

　　回归的数据集中的变量（Ｘｉ）是否有贡献（Ｔｔｅｓｔ）　

　　回归的可预测性Ｒ２（ａｄｊｕｓｔｅｄ　Ｒ２）高低

　　回归的数据集中的变量（Ｘｉ）是否存在多重共线性（ｍｕｌｔｉｃｏｌｌｉｎｅａｒｉｔｙ）或者说是否是奇异矩阵（Ｓｉｎｇｕｌａｒ　Ｍａｔｒｉｘ）

　　存在多重共线性（或者说奇异矩阵）怎么办？　　

好吧，首先来看看检验训练集和测试集是否来自同一个分布？

#训练集与测试集是否同分布KS检验
#假设H0: 训练，测试数据来自于同一个总体（分布），小于alpha则拒绝假设H0，大于alph则不能拒绝。
#H0: 相关变量将用于加入训练
#H1: 相关变量将从训练集中移出
#scipy.stats.ks_2samp
#a two-sided test for the null hypothesis that\
#   2 independent samples are drawn from the same continuous distribution.

import numpy as np
import pandas as pd
from scipy import stats
train = pd.read_csv("train.csv.gz")
test = pd.read_csv("test.csv.gz")
alpha =0.05 #设显著水平为0.05，

cols = train.drop(["SalePrice"],axis=1).select_dtypes(include = [np.number]).columns
cols_differ = {"ksvalue":[],"pvalue":[]}
for col in cols:
    pvalue = None
    ksvalue = None
    ksvalue, pvalue = stats.ks_2samp(train[col],test[col])
    cols_differ["ksvalue"].append(ksvalue)
    cols_differ["pvalue"].append(pvalue)

KStest_df = pd.DataFrame(cols_differ,columns=["ksvalue","pvalue"],index=cols).sort_values(by="pvalue")
KStest_df["Same_distribution"] = KStest_df.pvalue>alpha
print(KStest_df["Same_distribution"].head())

Id False
2ndFlrSF True
GrLivArea True
TotRmsAbvGrd True
TotalBsmtSF True
Name: Same_distribution, dtype: bool

从上面的KS test 可以看出，除了Id 以外的Feature 列都通过了Kstest (预设显著性水平为0.05，两侧检验）

看来，训练集和测试集是相关。把Ｉｄ列删除了，就能玩。

２．用统计方法，来看看（采用经典二乘法）下面这些情况。

　　回归的整体结果是否有意义（Ｆｔｅｓｔ）　

　　回归的数据集中的变量（Ｘｉ）是否有贡献（Ｔｔｅｓｔ）　

　　回归的可预测性Ｒ２（ａｄｊｕｓｔｅｄ　Ｒ２）高低

上面列了许多问题，其实用Ｐｙｔｈｏｎ测试起来非常简单。ｐａｎｄａｓ＋Ｓｔａｔｓｍｏｄｅｌ就可以搞定。　我在Kaggle HousePrice : LB 0.11666（前１５％）, 用搭积木的方式（2.实践-特征工程部分）一文中，最后一个ｔｅｓｔ函数中已经写好了这部分内容。只要把注释去掉，就可以解锁新的姿势。　哈哈

def pipe_r2test(df):
    import statsmodels.api as sm
    import warnings
    warnings.filterwarnings('ignore')
    print("****Testing*****")
    train_df = df
    
    ntrain = train_df["SalePrice"].notnull().sum()
    train = train_df[:ntrain]
    X_train = train.drop(["Id","SalePrice"],axis =1)
    Y_train = train["SalePrice"]
　　# 此处删除无关的代码
   
    result = sm.OLS(Y_train, X_train).fit()

    
    result_str= str(result.summary())
    results1 = result_str.split("\n")[:20]
    #此处解锁20行信息，用来解释
    for result in results1:
        print(result)
    print('*'*20)
    return df

其他函数不变。下面用搭积木的方式来生产两个预处理文件并比较测试。

注：pipe_PCA是一个新函数。这两天刚刚做出来的特征函数之一。基于statsmodels库，当然sklearn 和scipy 也有同样的库，我只是选用了其中的一个方法而已。

pipe_basic = [pipe_fillna_ascat,pipe_drop_cols,\
              pipe_drop4cols,pipe_outliersdrop,\
              pipe_extract,pipe_bypass,pipe_bypass,\
              pipe_log_getdummies, \
              pipe_bypass,
              pipe_drop_dummycols,pipe_bypass,      
              pipe_r2test,pipe_bypass]
pipe_basic_pca = [pipe_fillna_ascat,pipe_drop_cols,\
              pipe_drop4cols,pipe_outliersdrop,\
              pipe_extract,pipe_bypass,pipe_bypass,\
              pipe_log_getdummies, \
              pipe_bypass,
              pipe_drop_dummycols,pipe_PCA,      
              pipe_r2test,pipe_bypass]

pipes=[pipe_basic,pipe_basic_pca]
tmp = None

for i in range(len(pipes)):
    print("*"*10,"\n")
    pipe_output=pipes[i]
    output_name ="_".join([x.__name__[5:] for x in pipe_output if x.__name__ is not "pipe_bypass"])
    output_name = "PIPE_" +output_name
    print(output_name)
    tmp =(combined.pipe(pipe_output[0])
                .pipe(pipe_output[1])
                .pipe(pipe_output[2])
                .pipe(pipe_output[3])
                .pipe(pipe_output[4])
                .pipe(pipe_output[5])
                .pipe(pipe_output[6])
                .pipe(pipe_output[7])
                .pipe(pipe_output[8])
                .pipe(pipe_output[9])
                .pipe(pipe_output[10])
                .pipe(pipe_output[11])
                .pipe(pipe_output[12],output_name)
             )

先上结论：

回归的整体结果有意义。Ftest 的概率=0，拒绝零假设（即：回归模型直线斜率=0）

Basic 小火车（Pipe测试）：有意义，Prob (F-statistic): 0.00
Basic_PCA小货车（Pipe测试）：有意义，Prob (F-statistic): 0.00

回归的数据集中较多变量（Ｘｉ）没有贡献

（P>|t|列，是计算出来的Xi的贡献概率。假定alpha=0.05,许多列都大于0.05.不能拒绝零假设）零假设，是该Xi的系数(coe) =0. 不能拒绝零假设，意味着很可能有没有这个Xi特征变量，对于回归来说都没有关系。

变量（　Ｘｉ）没有贡献，往往意味着可以直接从模型中删除，这样可以提高计算的速度和降低噪音。不过如何删除就是另一个特征工程话题。可以通过ｆｅａｔｕｒｅ　ｓｅｌｅｃｔｉｏｎ　或者ＰＣＡ方式。　下文小火车２（Ｂａｓｉｃ＿ＰＣＡ）就展示ＰＣＡ进行了正交处理的功能。

例如：

Basic 小火车（Pipe测试）：绝大多数Xi(变量)变量没有贡献

BsmtCond （0.9597，概率非常大）没有贡献，
BsmtFinSF2 （0.0515，概率大于alph),没有通过t-test, 也认为没有贡献。

Basic_PCA小火车：前10的Xi，有贡献，排名靠后的Xi 没有贡献。

comp_000~comp_007（只显示了前7个变量）（0，概率很小）拒绝零假设，有贡献。
comp_21８（0.1159，概率大于alph),没有通过t-test, 也认为没有贡献。

回归的可预测性Ｒ２（ａｄｊｕｓｔｅｄ　Ｒ２）一样。

为了展示方便，小火车Ｂａｓｉｃ＿ＰＣＡ管道没有进一步处理，故两者Ａｄｊｕｓｔｅｄ　Ｒ２　一样。

Basic 小火车（Pipe测试）： 0.937
Basic_PCA小火车： 0.937

回归的数据集中的变量（Ｘｉ）存在多重共线性（ｍｕｌｔｉｃｏｌｌｉｎｅａｒｉｔｙ）是奇异矩阵（Ｓｉｎｇｕｌａｒ　Ｍａｔｒｉｘ）

Statsmodel 提供了Condition number 作为共线性和奇异矩阵的判断标准。这两个处理后的数据都有非常严重的共线性。

The condition number is large (1e+18)

The condition number is large (1e+16)

从上面可以看出，通过传统的统计方法（上古魔法），可以打开数据集的黑盒子。可以达到如下目标：

1。检验训练集和测试集是否相同分布。相同分布，是统计方法和机器学习的共同前提。这可以帮助预判后面的机器学习的训练，调参和stacking是否有意义？

2。检查变量间是否存在共线性关系(奇异矩阵，不满秩) ? 后期机器学习，或者预处理，应该采用什么样的方式正则化处理?

例如：

直接用PCA降维。
是否需要采用Normalzier来正则化处理
Lasso(L1）还是Ridge(L2),
XGBoost，lightGBM应该怎么结合L1,L2

3. feature 选择时的两种方法机器学习参数（lasso, randomforest) 还是用统计检验发现的概率(p value)

输出摘要：

1.小火车 - pipe_basic 测试结果

Results: Ordinary least squares
======================================================================
Model: OLS Adj. R-squared: 0.937
Dependent Variable: SalePrice AIC: -2375.2359
Date: 2017-12-11 14:27 BIC: -1249.5690
No. Observations: 1458 Log-Likelihood: 1400.6
Df Model: 212 F-statistic: 103.5
Df Residuals: 1245 Prob (F-statistic): 0.00
R-squared: 0.946 Scale: 0.010039
----------------------------------------------------------------------
Coef. Std.Err. t P>|t| [0.025 0.975]
----------------------------------------------------------------------
1stFlrSF 0.0545 0.0453 1.2037 0.2290 -0.0343 0.1434
2ndFlrSF 0.0099 0.0064 1.5336 0.1254 -0.0028 0.0225
3SsnPorch 0.0036 0.0044 0.8201 0.4123 -0.0050 0.0123
BedroomAbvGr -0.0086 0.0060 -1.4314 0.1526 -0.0204 0.0032
BsmtCond -0.0015 0.0298 -0.0505 0.9597 -0.0599 0.0569
BsmtFinSF1 0.0052 0.0024 2.1491 0.0318 0.0004 0.0099
BsmtFinSF2 -0.0055 0.0028 -1.9492 0.0515 -0.0110 0.0000
BsmtFinType1 -0.0040 0.0033 -1.2350 0.2171 -0.0104 0.0024
SaleType_ConLD 0.1221 0.0391 3.1193 0.0019 0.0453 0.1989
SaleType_Oth 0.0685 0.0620 1.1049 0.2694 -0.0531 0.1901
----------------------------------------------------------------------
Omnibus: 367.835 Durbin-Watson: 1.937
Prob(Omnibus): 0.000 Jarque-Bera (JB): 2577.551
Skew: -0.986 Prob(JB): 0.000
Kurtosis: 9.208 Condition No.: 1258412771503278080
======================================================================
* The condition number is large (1e+18).
The condition number is large (1e+16).

2.小火车 - pipe_basic_pca 测试结果

Results: Ordinary least squares
===================================================================
Model: OLS Adj. R-squared: 0.937
Dependent Variable: SalePrice AIC: -2374.1451
Date: 2017-12-11 14:27 BIC: -1222.0541
No. Observations: 1458 Log-Likelihood: 1405.1
Df Model: 217 F-statistic: 101.4
Df Residuals: 1240 Prob (F-statistic): 0.00
R-squared: 0.947 Scale: 0.010019
-------------------------------------------------------------------
Coef. Std.Err. t P>|t| [0.025 0.975]
-------------------------------------------------------------------
comp_000 -304.5691 4.4819 -67.9555 0.0000 -313.3620 -295.7761
comp_001 50.8477 0.7465 68.1139 0.0000 49.3832 52.3123
comp_002 3.7843 0.2682 14.1078 0.0000 3.2580 4.3105
comp_003 -798.4617 12.1768 -65.5722 0.0000 -822.3511 -774.5722
comp_004 -547.5712 8.2157 -66.6491 0.0000 -563.6894 -531.4529
comp_005 -989.4200 15.0826 -65.6002 0.0000 -1019.0102 -959.8298
comp_006 -2017.9360 30.6820 -65.7693 0.0000 -2078.1305 -1957.7416
comp_007 -190.4264 2.8626 -66.5213 0.0000 -196.0425 -184.8102
comp_218 0.3263 0.2075 1.5731 0.1159 -0.0807 0.7334
comp_219 -0.3834 0.3258 -1.1768 0.2395 -1.0225 0.2558
-------------------------------------------------------------------
Omnibus: 357.382 Durbin-Watson: 1.941
Prob(Omnibus): 0.000 Jarque-Bera (JB): 2423.551
Skew: -0.963 Prob(JB): 0.000
Kurtosis: 9.015 Condition No.: 10685794842663918
===================================================================
* The condition number is large (1e+16). This might indicate

最后，本人水平有限，试图下列内容用短短一篇文章表达处理。

商务与经济统计，
Python for probility, statistics, and machine learning
知乎中统计和机器学习的讨论

能力与愿望可能不太匹配。文章必然有大量的欠缺之处，或者逻辑跳跃不连贯，甚至基本概念错误。期望知乎的朋友多多指点。

分享是对自己最好的投资。

Kaggle HousePrice : （前１５％）,（2.实践-特征工程部分-之上古魔法-统计检验）

文章被以下专栏收录

AIGC开发者