抽象代数|笔记整理(A)——二次扩域,有限域,分裂域
大家好,不出意外,这是我们的最后一节正课的内容。因为我们现在是校历的第十五周,大部分的专业课都迎来了结课。抽代也不例外,所以我们的笔记内容也就到此为止了。
事实上,抽代的内容也不只是这么点,这些只是一些代数学的基础内容。不过之后的相关研究和内容,就是按照自己的研究需要去自己学了。
我们学校还有一门代数学的课,但是因为开课时间大约是一年多以后,并且我也不一定需要学代数学(毕竟主修方向不是基础数学,可能还要花点时间学点应用的东西)。所以续上这一系列笔记的概率不大。但是我保证,如果我能够有时间修代数学,我还会尽力去完善和补充这笔记上的内容!
最近也注意到了一些评论,私信中也看到了一些评论和问题。因为我自己的实力,扩展和解答的能力不足,所以很多问题我自己是解决不了的。不过我会通过邮件联系Prof,将一些我觉得有意思的题目反馈给她,希望不会让大家失望。
当然有人问,笔记标号上的A是smg?之前作为一个程序员,省字节的习惯还没有改掉,10给我的感觉很臃肿,于是我决定改用十六进制表示,用A表示10的意思啦。希望大家理解一个程序员的修养,哈哈。
废话少说,我们继续我们的内容。
提供之前的笔记:
- 抽象代数|笔记整理(1)——群,子群,同态
- 抽象代数|笔记整理(2)——同构,划分,陪集
- 抽象代数|笔记整理(3)——陪集与阶,直积,商群,群作用
- 抽象代数|笔记整理(4)——轨道,中心,西罗子群
- 抽象代数|笔记整理(5)——群阶数,西罗定理
- 抽象代数|笔记整理(6)——环,多项式环,理想
- 抽象代数|笔记整理(7)——商环,整环与分式域,极大理想
- 抽象代数|笔记整理(8)——序,代数几何引入,模
- 抽象代数|笔记整理(9)——域,域的扩张
我们开始我们的内容
目录
- 特征,二次扩域
- 有限域,分裂域
特征(Characteristic),二次扩域(Quadratic extension)
二次扩域是扩域中一个特殊的情况,有一些有趣的性质,这里我们简单提一下。
在这之前需要给一个之后要用的定义
Definition:Characteristic
设 F 是一个域,如果 p 是满足 p.1=1+1+...+1=0 的最小的正整数( 1 是域中的单位元),那么我们定义 p 是这个域的特征。记作 Char(F)=p 。如果这样的 p 不存在,我们认为定义它的特征为 0 。
特征其实部分描绘了域的结构。另外我们有必要说一下,因为之后的内容大部分都与数域会有联系,因此我们用 1 表示单位元,会使符号表示更友好一些。
例子也不难说,比如 Char(F_p)=p,Char(Q)=0 。
虽然这挺显然的,但我们有必要提一下,特征只有两种情况:0和素数(想想为什么)。
下面就是关于二次扩域的最基本的性质了。
Proposition:
设 F 是一个域, Char(F) \ne 2 ,那么任意的域的二次扩张 K (也就是说 [K:F]=2 )可以通过连接一个平方根得到。也就是说 K=F(\delta) ,且 \delta^2=d \in F 。反过来,如果 \delta 是在 F 的域的扩张里的一个元素,同时满足 \delta^2 \in F,\delta \not \in F ,那么 F(\delta) 就是 F 的一个二次扩域。
我们证明一下这个结论。
我们注意到这是个二次扩域,二次扩域就意味着有两个基,于是我们可以通过基的构造,构造二次方程,找到这个 \delta 。
因为 [K:F]=2 ,我们可以设基为 \{1,\alpha\} ,其中 \alpha \in K 且任意,并且 \alpha^2 \in K ,这样的话,因为 \{1,\alpha\} 是这个扩域的基,我们可以说明存在 a,b \in F ,使得 \alpha^2=a+b\alpha ,注意到这就是一个二次方程,我们配方可以得到 (\alpha-\frac{b}{2})^2=\frac{b^2}{4}+a \in F
那么我们考虑令 \alpha-\frac{b}{2}=\delta ,这样的话,因为 \alpha \in K,\frac{b}{2} \in F \subset K ,于是 a-\frac{b}{2} \in K,也就是 \delta \in K 并且根据等式,有 \delta^2 \in F ,于是我们有 F(\delta) \subset K ,下面只需要证明反方向的包含关系,就可以部分得到我们的结论。
证明反方向的包含关系,意味着只需要证明对于任意的 x \in K ,有 x \in F(\delta) 就可以了。而这并不难说,因为我们有一个现成的 \alpha 。因为 \alpha=\frac{b}{2}+\delta ,而 \frac{b}{2} \in F \subset F(\alpha) ,于是 \alpha \in F(\delta) ,这样的话就证明了 K \subset F(\delta) ,于是乎 K=F(\delta) ,就证明了结论。
事实上,如果 \delta \not \in F, \delta^2 \in F ,那么 \{1,\delta\} 就是 F(\delta) 在 F 下的一个基,于是 [F(\delta):F]=2 ,所以确实这是个二次扩域。
这就是关于二次扩域的基本内容了。
下面这个性质给扩域与子域建立了一个简单的联系。
Proposition:
设 K 是 F 的一个域的扩张,那么所有的在 K 内是 F 上代数数的元素构成的集合构成 K 的一个子域。
这个证明需要用一个证明子域的一个思想。反过来,它也可以被用在证明子群,子环的一些习题中。
不妨设 \alpha,\beta \in K ,并且是 F 上的代数数,那么注意我们这里只需要证明 \alpha-\beta ,\alpha\beta^{-1} 都是 F 上的代数数即可(这就是技巧,想想为什么)。
那么我们再将假设做的大胆一些,事实上只需要考虑构造出来的域 F(\alpha,\beta) 即可,这是因为这个域更好想,并且也涵盖了我们要研究的两个对象。
我们知道,如果考虑它在 F 下的维数,如果这是个代数扩张,那么它一定是个有限数(但是,并不代表如果是无限数,这就不是个代数扩张,上一节我们举过反例)。所以我们根据公式 [F(\alpha,\beta):F]=[F(\alpha,\beta):F(\beta)][F(\beta):F] 可知左式是一个有限数(因为右边的第一项相当于添加了一个 \alpha ,而第二项相当于添加了一个 \beta ,当然不会让维数变成无限大),于是我们可知这确实是一个代数扩张。
也就是说,扩张的元素在 F 下都是代数数。而我们要考察的元素 \alpha-\beta,\alpha\beta^{-1} 都是在这个代数扩张的域内的。所以这就说明了结论成立。
下面回到特征,看看特征的相关性质。
Proposition:
设 F 是一个域,如果 Char(F)=0 ,那么 F 包含一个子域与 \mathbb{Q} 同构,如果 Char(F)=p ,那么 F 包含一个子域与 \mathbb{Z}/p\mathbb{Z} 同构。
我们证明一下这个结论。
又到了证明同构的时候,证明同构的题目见了很多很多了,基本思路都是:找映射,找映射规则,找核空间。这个地方也不意外。
先考虑特征为0的情况,我们构造一个映射 \phi:\mathbb{Q} \to F ,如何构造映射规则呢?
不知道之前的笔记有没有注意过,在构造分式域的时候,我们考虑的也是最直接和最本质上的映射,那么对于任意的 \frac{n}{m} \in \mathbb{Q} ,对应到哪里合适?显然就是 (n.1)(m.1)^{-1} (注意我们的写法)。因此这就是我们的映射规则了。
下面的事情都是顺其自然:证明映射无缺陷(well-defined),证明映射是个同态。我们不再写出详细证明。
之后我们考虑核空间 Ker ,因为 Ker \phi=\{n/m \in Q \mid (n.1)(m.1)^{-1} =0\} ,这个要注意到的是,显然 (m.1)^{-1} \ne 0 (分母不为0),而且满足 n.1=0 的 n 只有 0 (因为它的特征为0,根据定义可以得到这个结论),所以我们就有 Ker \phi =\{0\} 。
另一方面,根据第一同构定理, Q/Ker \phi \simeq Im\phi ,所以 Q \simeq Im \phi ,显然, Im\phi 是一个 F 的子域,这就证明了结论。
如果特征是p,那么我们考虑的映射是 \varphi:\mathbb{Z} \to F,映射规则为 n \to n.1 ,那么我们只需要考虑 Ker ,也就是说证明 Ker \varphi=p\mathbb{Z} 就行了。带余除法一下挺显然的,我们之前也做过类似的题目的讨论,这里就不给出详细的证明了。
这个性质比较重要的原因是,对于任意的域,我们都可以找到它的子域,与这两个数域是同构的。我们用一个定义来补充说明一下它的意义。
Definition:prime field
诸如 \mathbb{Q} , \mathbb{Z}/p\mathbb{Z} 这样的没有非平凡子域的域称为素域。
其实这个性质就是想告诉我们,任何一个域,都是一个素域的扩张。
有限域(finite field),分裂域(splitting field)
通过这个性质,我们也有办法去刻画一个有限域的元素个数和它的相关结构。具体的分析如下。
设 K 是一个有限域,那么它的特征不可能为 0 ,这样的话就应该是一个素数 p 。我们根据上面的那个性质,可以知道 K 包含一个子域是 F_p (有 p 个元素)。我们设 [K:F_p]=n ,也就是说把这个有限域 K 看作了 F_p 上的一个向量空间。
再设 \{u_1,...,u_n\} 是基,那么对于任意的 \alpha \in K ,就有 \alpha =a_1u_1+...+a_nu_n ,根据排列组合理论我们就能得到 |K|=p^n ,并且我们也能得到每个元素的形式。
至于分裂域概念的产生,也是基于一些比较自然的想法:我可不可以根据一个已知而给定的域,通过增添一个多项式的根,得到一个我需要的新的域的扩张?
这个想法促进了分裂域的产生。它的正式定义如下:
Definition:splitting field
设 F 是一个域, f(x) \in F[x] 是一个系数为正的多项式, K 是 F 的一个域的扩张。如果一个多项式 f(x) 可以写成一系列在 K[x] 的一次多项式的乘积,则称 K 是 F 上关于 f(x) 的分裂域。
翻译过来就是说,我们把多项式表示为 f(x)=u(x-u_1)(x-u_2)...(x-u_n),u,u_i \in K ,并且 K=F(u_1,...,u_n)
比如说,对于有理数域 \mathbb{Q} ,我们如果想让这个域扩大一些,让它含有 x^2-2=0 的根,那么就需要添加两个数 \sqrt{2},-\sqrt{2} 。这样的话根据定义我们把域写成 \mathbb{Q}(\sqrt{2},-\sqrt{2}) ,也就是 \mathbb{Q}(\sqrt{2}) 即可。
下面这个性质刻画了分裂域的一个性质
Proposition:
设 F 是一个域, f(x) \in F[x] , deg(f(x)) \ge 1 ,那么存在一个关于 f(x) 的分裂域,并且任意两个分裂域都是 F-isomorphic (F-同构)的
这是什么意思呢?就是说,任意两个 f(x) 的分裂域,它们都是同构的。代数学中,同构与相等的区别其实不大,事实上我们一般认为,如果两个代数结构同构,就可以把它们理解为一个东西。
我们不再证明。
看到这里可能大家容易直觉上产生一个想法:既然多项式是给定的,那么它的根也就给定了,为什么它的分裂域不是相等的呢?
这个想法也是困扰了Prof一天的时间,最终她给了一个精妙绝伦的例子!
考虑一个矩阵集合 M_2(\mathbb{C})=\{[\begin{smallmatrix}a & b \\ c & d \end{smallmatrix}] \mid a,b,c,d \in \mathbb{C}\} ,并且设域 F 为所有形式为 \begin{bmatrix} a & 0 \\ 0 & a \end{bmatrix} 的矩阵集合,其中 a \in \mathbb{R} 。并且设多项式为 f(x)=x^2+1 (注意这里的 1 是指 F 内的单位元,也就是单位矩阵),这样的话考虑两个根 \alpha=\begin{bmatrix} i & 0 \\ 0 & i \end{bmatrix},\beta=\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} ,事实上经过计算,它们都是 f(x) 的根,但是很明显,经过演算,可以得到 F(\alpha),F(\beta) 是不同的两个域。
也就是说,多项式给定,对应的根却不一定给定!这个性质只是在数域上成立的,矩阵域上可没有这么好的性质。
我们可以把相似的思想用法,再用回到有限域的情况。
Theorem:
设 p 是一个素数, n 是一个正整数,那么存在一个域它的元素个数为 p^n ,并且在同构意义下唯一。
这个证明方法还是很奇特的,不过学过竞赛的人会对这样的构造略有眼熟。
首先看到这个元素个数就要想到我们之前对于有限域的讨论。显然 p 是之前那个未扩张有限域的元素个数。所以我们这里构造的时候考虑的域就不是我们一般考虑的数域 F ,而是 F_p 。
另外,再看看这个定理,为什么要提“同构意义下唯一”?是不是很眼熟?对的,这提示我们证明要考虑一个多项式的分裂域,因为分裂域是具有这样的性质的。
有了这些前提,就可以开始写证明了。
我们考虑一个多项式 f(x)=x^{p^n}-x ,那么按照多项式理论应该是有 p^n 个根的。那么我们的思路很简单,就是考虑证明,这 p^n 个根连接原来的域 F_p 构成的域 K 构成 F_p 上的一个分裂域。
证明它的第一件事,就是考虑它是不是真的有 p^n 个根。也就是说,是否它们是互异的?答案是肯定的,我们考虑一下,假如有一个根 \alpha 它的次数比一次要大,那么我可以把多项式写成 f(x)=(x-a)^2g(x) 。求导一下就有 f'(x)=2(x-a)g(x)+(x-a)^2g'(x) 。也就是说 f'(a)=0 。
但是另一方面呢?我们考虑这个多项式本身求导,有 f'(x)=p^nx^{p^{n}-1}-1 ,我们要注意的是我们考虑的域是 F_p ,所以其实 f'(x)=-1 ,也就是说 f'(a)=-1 ,这就矛盾了。也就是说,它的所有根都是互异的。
好的,再看看这集合它为什么是一个域。我们要证明它是一个域,需要做的工作是什么?
我们在之前证明子域的时候,考虑的都是常规操作。这次我们和之前一个例子一样,考虑非常规的操作。
我们假设这个集合是 E ,那么对于任意的 \alpha,\beta \in E ,只要证明 \alpha-\beta,\alpha\beta^{-1} 都在这个域内就可以了。也就是说,它们俩都是方程 x^{p^n}-x=0 的根。
首先因为 \alpha,\beta \in E ,所以 \alpha^{p^n}=\alpha,\beta^{p^n}=\beta ,我们注意到 (\alpha\beta^{-1})^{p^n}=\alpha^{p^n}\beta^{-p^n}=\alpha\beta^{-1} (对不起,我有必要说一下,因为这里考虑的都是多项式了,所以我们有必要说明这个域乘法意义下是交换的,否则这个运算是不合法的), (\alpha-\beta)^{p^n}=\alpha^{p^n}-\beta^{p^n}=\alpha-\beta (这是因为,二项式展开后,除了这两项,其余项都是 p 的倍数,那么在特征为 p 的域下这一项就是0)。所以,我们就可以得到它确实是一个域。
好的,我们知道了 E 是一个域,有什么好处?因为我们已经找到了这个有 p^n 个元素的域 E ,所以现在要证明构造出来的这个东西,确实它就是 K ,应该如何去做?
回想定义, K 是 F_p 域上关于 f(x) 的一个分裂域,也就是说, K 中要含有 F_p 和那 p^n 个根。那么我们只需要证明 F_p 里的每个元素,都是在 E 中的就可以了。
直接代入那些元素我觉得有些太不友好了,事实上考虑一下 E 作为一个域的性质,这个域内有单位元 1 ,并且它确实是 f(x)=0 的根。但是 F_p 中的单位元也是 1 ,这就说明了 F_p 的所有元素都是 f(x)=0 的根(因为我可以用这个单位元生成整个 F_p ),这样的话就说明了这个结论是对的。也就是 K=E 。
综上,我们确实就说明了这个分裂域是存在的,并且因为它是分裂域,所以同构意义下唯一。
如果不放心这个唯一性,还可以考虑这么证:因为 K\backslash\{0\} 是一个乘法群,并且有 p^n-1 个元素,这就意味着对于这个群内的任意的一个元素 x ,有 x^{p^n-1}=1 。那么 x^{p^n}=x ,也就是说群内的所有元素都是它的根, 0 手工验算也是,所以这个集合确实涵盖了所有的 f(x)=0 的根。也就满足了分裂域的定义。
这个证明总体还是很巧妙的,也运用了很多多项式内的相关性质和内容。我觉得难理解的地方在于域的变化,因此有点反直觉(不过下面这个会让你有更强烈直观的反直觉的感觉)。看着累了烦了的没关系,我们之后提供两个Prof用来润滑的例子来休息一下,然后给出我们正文的最后一个大定理。
先来看第一个吧。
Example:
通过考虑 F_2 ,表示出一个4阶的域的所有可能的元素形式。
简单粗暴的一个题。
我们设这个有限域为 K ,那么我们很容易知道的是 [K:F_2]=2 (根据之前对有限域的讨论),那么我们考虑的就是 F_2(x) (这么写的原因是,二次扩张只需要添加一个元素就可以,有之前的二次扩域的性质保证)。现在的问题是找到满足分裂域相关性质的那个多项式。先不妨设它是 f(x)=ax^2+bx+c 吧。要注意的是,涉及到扩张维数的时候,对应的扩张的多项式要在 F_2 下是不可约的,也就是说,在这个域的意义下, 0,1 都不能作为根存在。
有了这些铺垫我们就好确定系数了,首先因为它要求二次,所以 a=1 。因为 0,1 不能作为根,所以 c \ne 0,1+b+c \ne 0 。开心的是,因为我们一直都是在 F_2 意义下讨论的多项式的值,也就是说如果不是0,那就是1。因此我们可以得到 c=1,1+b+c=1 ,那么可以得到 b=1 。这样的话多项式就确定了下来是 f(x)=x^2+x+1 。
结合我们之前说的性质 F_2(x)/(x^2+x+1) \simeq F_2(\alpha) ,结合 F_2(\alpha)=\{0,1,\alpha\} ,我们容易得到, F_2(x)=\{0,1,\alpha,\alpha+1\} ,其中 \alpha 是多项式在 F_2 意义下的根。这就是我们要的答案。
还有一个例子是这样的
Example:
设 K 是一个有限域,证明所有的域中的非零元素之积为-1
根据讨论我们知道, K 的阶数一定是 p^r 个,那么我们不妨这么设,然后考虑乘法群 K ^{\star}=K \backslash \{0\} ,这样就有 |K^*|=p^r-1 。注意到群的性质,我们可以知道这个群里任何一个元素,它都是 x^{p^r-1}-1=0 的根。
看到非零元素之积,学过高代的人要有印象,这需要联想到韦达定理。
根据韦达定理,所有非零元素之积为 (-1)^{p^r-1}*(-1)=(-1)^{p^r} ,也就是说,除了 p=2 的情况,其余的都已经证好了。
p=2 的情况呢?别忘了, p=2 说明考虑的域是 F_2 ,这说明 -1=1 ,想明白了吗?
当然,不要在公车上和人讨论这个定理,一个 -1=1 说出来,别人就有可能把我们当成傻子……
好啦,让我们欢迎我们这一系列笔记中最后一个大定理!
Theorem:
设 \varphi: F \to F' 是一个域之间的同构, f(x)=a_nx^n+...+a_1x+a_0 , g(x)=\varphi(f(x))=\varphi(a_n)x^n+...+\varphi(a_1)x+\varphi(a_0) 。设 E 是 F 下关于 f(x) 的分裂域, E' 是 F' 下关于 g(x) 的分裂域,那么这个同构 \varphi 会拓展到同构 \sigma: E \to E' 。
我们证明一下这个结论,这个结论的证明我们考虑的是对 deg(f(x)) 进行归纳。在这之前,先来考虑一些很简单的情况。
如果 f(x) 的每一个不可约的因子都只是一次的,那么此时 f(x) 它的所有的根都是在 F 内的,对另一边也是同理(想想为什么,这需要用到域扩张维数的一个性质)。那么这个时候很平凡, E=F,E'=F',\varphi=\sigma 。
如果 f(x) 至少含有一个不可约因子 p(x) ,满足 deg(p(x))\ge 2 ,这个时候考虑 q(x)=\varphi(p(x)) ,同构意义下它当然也是不可约的。设 \alpha \in E 是 p(x) 的一个根, \beta \in E' 是 q(x) 的一个根,那么我们可以根据之前的定理(应该是上一节),说明可以把这个同构 \varphi 扩展到一个新的同构 \sigma':F(\alpha) \to F'(\beta) 上,满足 \sigma'|_F=\varphi,\sigma'(\alpha)=\beta ,并且 f(x)=(x-\alpha)f_1(x) \in F(\alpha)[x],g(x)=(x-\beta)g_1(x)\in F'(\beta)[x]
确实,我们通过一种类似一个一个消除的方法,来不断的降低多项式的次数,进而使我们有办法能够对次数进行归纳。但现在我们还需要说的就是, E 确实是在 F(\alpha) 意义下关于 f_1(x) 的分裂域。而根据我们之前的证明,其实证明这个结论就差了一步:证明它是最小的那个扩域。
而这是很显然的,因为所有的 f_1(x) 的根都是在 E 内的,如果这些根都包含在一个更小的满足条件的域 L 内,也就是说 L 同时还要包含 F(\alpha) ,那么这样的话, L 就包含了 f(x) 与 F 的所有东西。这会发生什么?别忘了, E 是我们给定的大的多项式下的分裂域,是有最小性的。如果 L 更小就矛盾了。因此这个结论就成立了。而对于 E' 上也是有个相似的结论的。
好的,回到归纳法,如果 deg(f(x))=n=deg(g(x)) ,那么这样做之后,就会有 deg(f_1(x))=n-1=deg(g_1(x)) 。这样的话,根据第二数学归纳法,我们就能得到,确实存在一个同构 \sigma:E \to E' ,它是 \sigma':F(\alpha) \to F'(\beta) 的扩张。这就证明了结论。
这个定理要是理解起来,也是挺有难度的。下面一张图或许可以给个相对直观的印象。
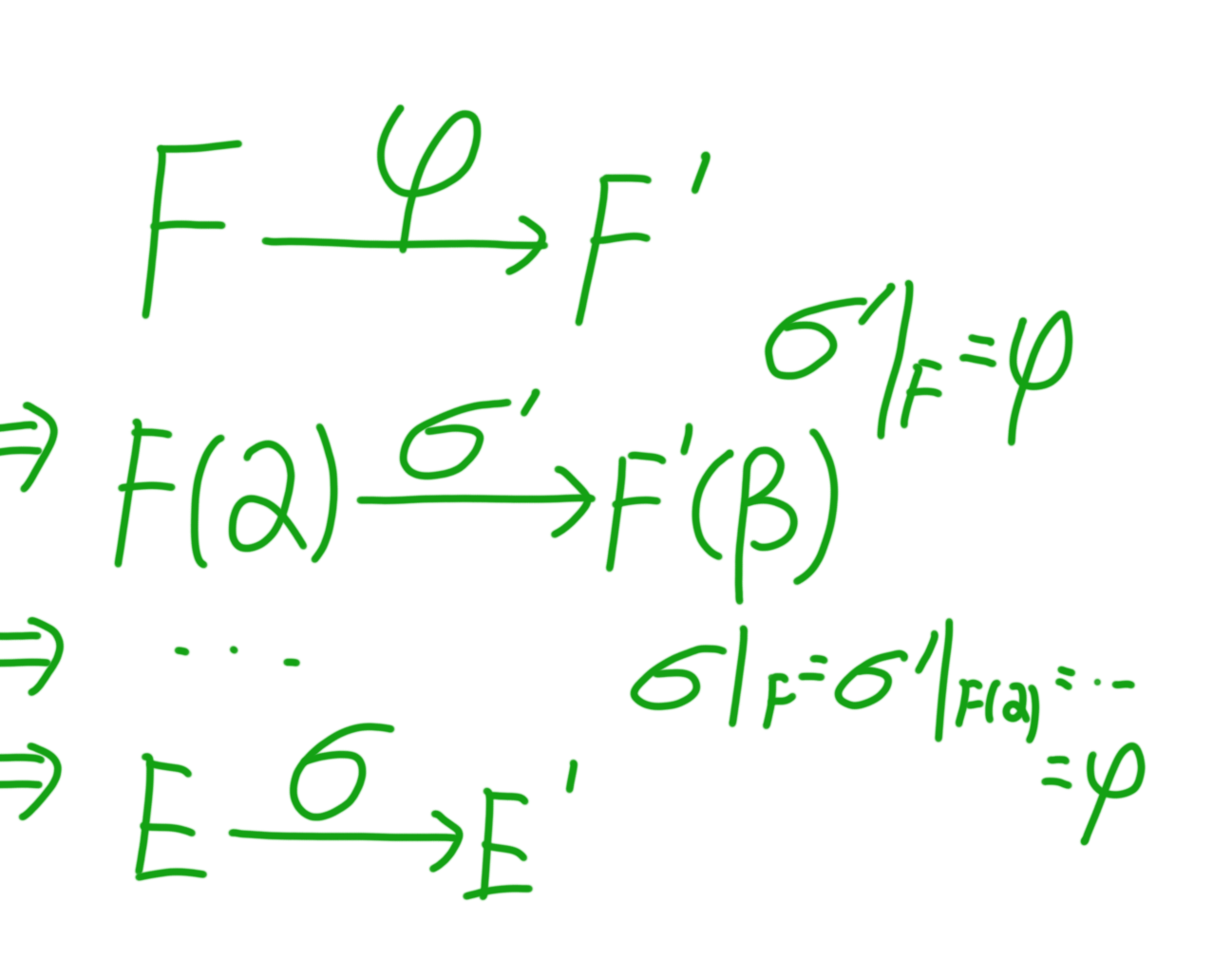
好的,以上就是我们这学期抽象代数的全部正文内容了。
小结
本节的内容在理解上可能还是会挺有难度,继续针对域的内容做了一些深入的介绍。不过也还好,正文的内容暂时就介绍到这里了。
事实上,如果做代数学的研究,这只是个基础了,剩下的,就是按需所学了。
在下一节中我们会提供一些相关的习题和答案,抱歉拖了这么久~~
不要问我为什么又是下一节。
——————————————————广告——————————————————

本专栏为我的个人专栏,也是我学习笔记的主要生产地。任何笔记都具有著作权,不可随意转载和剽窃。
专栏目录:笔记专栏|目录
想要更多方面的知识分享吗?欢迎关注专栏:一个大学生的日常笔记。我鼓励和我相似的同志们投稿于此,增加专栏的多元性,让更多相似的求知者受益~

