CS 294: Deep Reinforcement Learning:IRL
Berkeley深度强化学习的中文笔记(专题补充):逆强化学习Inverse Reinforcement Learning
在CS294的秋季课程中加入了一些新的内容,其中把逆强化学习课程内容完全翻新了,更为清晰,完整,连贯,因此值得系统学习一下。这一专题分成两个部分,分别对应两堂课的内容:1.Connections Between Inference and Control 2.Inverse Reinforcement Learning,前者用概率图的观点建立了优化控制与强化学习(Q-learning,policy gradient)之间联系,也可以解释人类动作,而它的推断过程又能引出第二部分逆强化学习。
Connections Between Inference and Control
问题的出发点是:我们用优化控制或强化学习得到的策略能用来解释人类的行为吗:
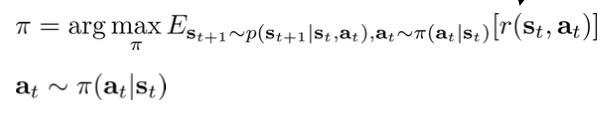
我们之前使用优化控制或强化学习来解决上式,可以得到最优的策略。然而问题是人类或动物的动作并不是最优的,而是具有一些偏差的:比如让一个人去拿桌子上的一个橘子,那手的轨迹一定不是一条从起点到目标的直线,而是有一些弯曲的轨迹,也就是带有偏差的较优行为,但是这种偏差其实并不重要,只要最后拿到橘子就行了,也就是说1.有过程中一些偏差是不重要的,但另一些偏差就比较重要了(如最后没拿到)。而且每次拿橘子的动作也是不一样的,因此2.人的动作带有一定的随机性。由此我们可以认为3.人类行为轨迹分布是以最优策略为峰的随机分布。
决策过程的概率图模型
为了解释人类的这种行为分布,如果再采用寻找最优的策略的思路就不太好了。为此我们引入概率图模型,虽然我们在第一节的时候就引入过这个概率图:

但是这次要引入另一种概率图(最优模型,只用来模拟最优路径),其含义更为抽象,需要讲解一下:
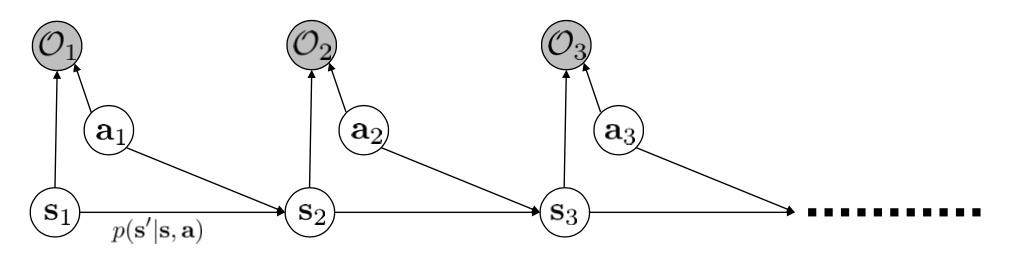
其中
- 新节点\mathcal{O_t}的含义比较抽象,引入它更多的是为数学上的解释(能让reward值以概率形式传播,而非只是Q-值),粗糙的含义是在s_t,a_t条件下人想要努力去获得当前奖励,称为optimality变量,只有0,1两种取值,取1的概率(人想要达到最优)同比与当前奖励p(\mathcal{O_t}|s_t,a_t)\varpropto exp(r(s_t,a_t))(奖励值高时人想要努力,低时人就不太想要努力),而且这个变量是可以被观测的。
- s_t不再是a_t的父节点了,也就是说这里没有显式的策略\pi(a|s),那s_t,a_t的关系就要看\mathcal{O_t}的取值了,从\mathcal{O_t}取最优值可以反推出s_t,a_t的关系。作为父节点,我们需要给出s_t,a_t的先验分布p(\tau)=p(s_{1:T},a_{1:T}),这个代表了在物理环境允许的情况下可以做出的动作分布(比如在室内做出飞行的动作概率很小)
现在可以考察一下如果人每一步都很想达到最优,那人的轨迹分布是:
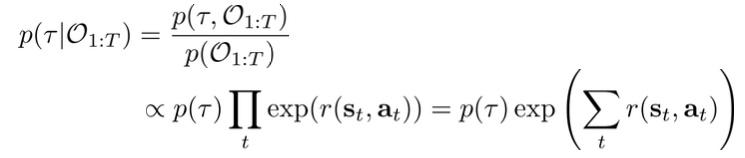
最后的两项:p(\tau)代表这条路径物理环境是否允许(即使很想要也总不能瞬间拿到橘子),exp(\sum_tr(s_t,a_t))代表这条路径的奖励值,因此人很想达到最优时,那奖励值越高的路径概率就越高。这两点都是十分合理的,而且最后得到的是一个路径分布,而非最优路径,因此这个分布能很好地解释人类的行为。
既然这个模型能很好地解释人类的行为,那我们是否能充分地利用它呢?对它利用有以下三点:
- 这个模型能模拟suboptimal的动作轨迹(也就是给出一个在最优动作附近波动的动作分布),那么这种模型对inverse RL有很大意义,因为人类数据都可以说是suboptimal的,而inverse RL要据此找到optimal的。
- 能用概率图的推断算法来解决控制和planning问题,联系了优化控制和强化学习
- 解释了为什么带有随机性的策略更好,这对exploration和transfer问题很重要。
概率图Inference = 值迭代
对于这个模型的利用采用概率图的推断算法,而有三种推断情形:

其推导过程有些复杂,需要一些概率图知识,为了避免舍本逐末,减轻阅读压力,把这三种推断情形的详细解释放到附录中。
推导的结论是:
后向信息等价于值函数:
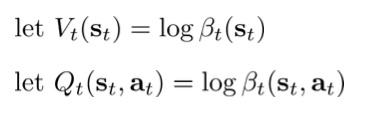
后向信息传播过程等价于值迭代过程。由后向信息传播导出的是soft max的值迭代:
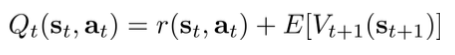
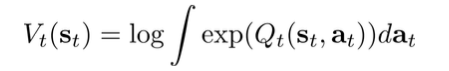
推断算法得出的policy等价于Boltzmann exploration:
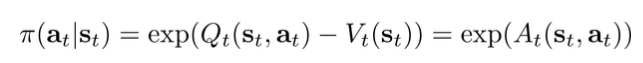
总结一下可以得到:
Q-learning with soft optimality
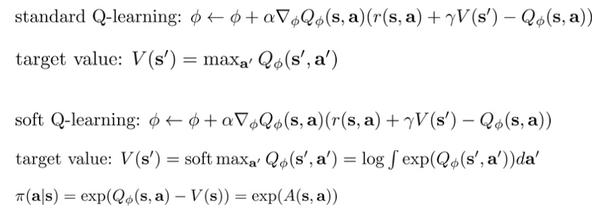
只是改成Boltzmann exploration的策略,对应的Q-值更新使用soft max,而且这个更新也是off-policy的。
Policy gradient with soft optimality
上面推导出的Boltzmann exploration的策略,与Policy gradient也有紧密联系:
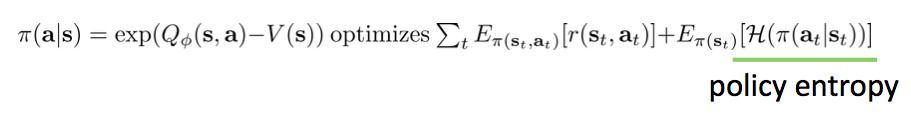
这是因为加入entropy项的Policy gradient目标等价于当前策略\pi(a|s)与最优策略\frac{1}{Z}exp(Q(s,a))的KL散度:
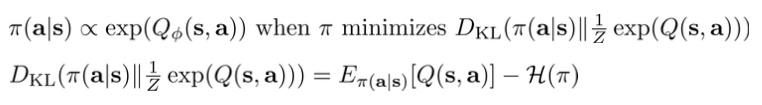
那么由此加入entropy项的Policy gradient与使用duel net的soft Q-learning有联系,对\pi的更新与对Q的更新方式十分相似,由于篇幅有限,具体内容查看paper《Equivalence between policy gradients and soft Q- learning》和《 Bridging the gap between value and policy based reinforcement learning》
Soft Q-learning
使用Q-learning with soft optimality时,在连续情况中有个小问题:Boltzmann exploration\pi(a|s)\varpropto exp(Q(s,a))无法直接采样,因为我们使用以下网络计算Q值,那么对于每一点我们只知道其概率值,而这个概率分布可能是十分复杂的,多峰的:
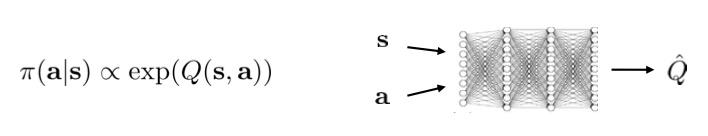
一种采样方法是利用SVGD,使用变分采样的方法:我们再训练一个采样网络,使其输出\pi(a|s)\varpropto exp(Q(s,a))

说白了,这个和GAN十分相似,采样网络就是conditional GAN的generator,而原Q网络相当于一个discriminator。
使用soft optimality的好处
- 增加exploration,避免policy gradient坍缩成确定策略
- (在一般情况中训练的soft optimality)更易于被finetune成更加specific的任务
- 打破瓶颈,避免suboptimal。
- 更好的robustness,因为允许最优策略以及最优路径有一定的随机性。训练Policy gradient时,不同的超参数选取很容易会落到不同的suboptimal动作中。
- 能model人的动作(接下来的inverse RL)
逆强化学习Inverse RL
之前我们的环境情形都是环境有一个客观的reward反应,或者可以根据人类的目的来设计一个reward函数,然而在很多的应用情形下这种客观的reward不存在,而且人类设计的reward也很难表示人类的目的,比如说想要机器学会倒水,甚至学会自然语言。但是我们有的是很多人类的数据,可以视为从一个最优策略分布中采样出的数据,那么我们是否可以根据这些数据来还原出reward函数,即知道人类的目的,然后使用这个reward来训练策略呢。
这个就是Inverse RL的思路,先根据数据得到reward函数,但是难点在于这些数据都是一个最优策略分布中采样出的,因此就像上一节所说的,这些样本是suboptimal,有随机性的。而且得到的reward函数也很难进行衡量。
传统上有对Inverse RL进行研究,但是由于传统研究方向和方法与当前的有很大的不同,所以将省略传统上对Inverse RL的研究。
既然上一节的概率图模型能很好地解释人类行为,那么是否这个模型能用来解决Inverse RL问题呢。
MaxEnt IRL算法
由于环境的reward并不知道,所以我们希望用一个参数为\psi神经网络来表示r_{\psi}(s_t,a_t),那么按照假设optimality变量p(\mathcal{O_t}|s_t,a_t)\varpropto exp(r_{\psi}(s_t,a_t)),应用之前的概率图的结论可以得到概率图模型下的最优路径分布:

现在我们希望能根据数据来训练reward网络,方法就是最大化数据路径的概率图模型下的概率似然:
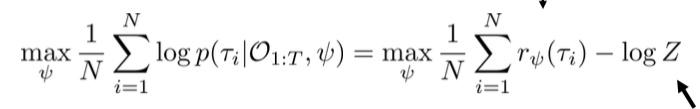
等式右边前一项已经很清晰了,就是最大化数据的reward,但麻烦的部分是后面的归一化项Z=\int p(\tau)exp(r_{\psi}(\tau))d\tau,为此我们对其先求导:
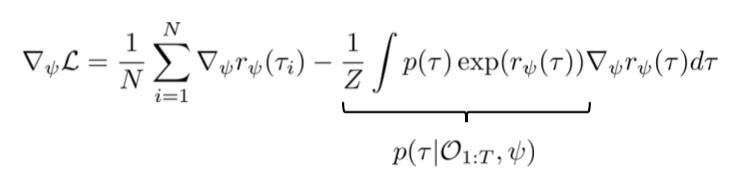
可以看到经过求导,后一项可以化成期望形式,就简单许多:

前一项是在增大数据分布的reward,后一项是在降低当前reward的最优模型给出的soft optimal策略。
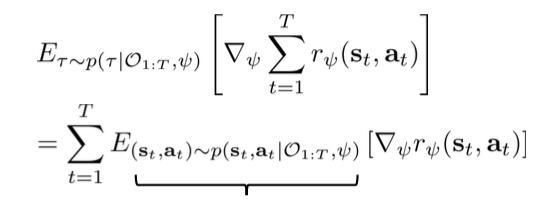

因此从之前的概率图模型知识可以知道最优模型给出的soft optimal路径分布同比于后向信息\beta_t与前向信息\alpha_t相乘。
这样一来Loss function导数中的两项我们都可以求了,那么就可以对reward网络进行更新:
The MaxEnt IRL algorithm:

称为Max Entropy算法是因为(在线性情况)这等价于优化max_{\psi}\mathcal{H}(\pi^{r_{\psi}}),s.t.E_{\pi^{r_{\psi}}}(r_{\psi})=E_{\pi^*}(r_{\psi}),即soft optimal策略与数据策略的平均reward相同时,熵最大的soft optimal模型。
sample-based MaxEnt IRL算法
直接采用概率图模型推导出的MaxEnt IRL有个问题:需要计算后向信息\beta_t与前向信息\alpha_t得到路径分布,并且做积分得到期望值,这对于大状态空间和连续空间是不可行的。因此一个想法是与其直接计算期望,不如用sample来估计。
因此改进方法为使用任一max-ent RL算法(如soft Q-learning,soft policy gradient)与环境互动,来得到当前reward下的路径样本,用这些路径来估计Loss function的后一项:

但这个方法也有一个显著问题:每一次更新reward网络,就要训练一遍max-ent RL算法,而RL算法训练常常需要成千上万步。因此与其每次reward更新时都训练一遍RL,不如每次reward更新时只改进一点原来的RL策略(由于reward每次更新很小,所以这个改进是合理的)。剩下的问题是有改进的RL路径样本对期望的估计成biased了,简单的方法是每次都用一个改进的RL路径样本batch来更新reward,但更data-efficient的方法是采用importance sampling(off-policy方法,在data-efficient专题再细讲)。
与behavior cloning差异:
Imitation learning中的behavior cloning也可以从数据中学习人类的行为,其直接对策略建模\pi_{\theta}(a_t|s_t),最优化数据行为在策略模型中的概率似然,等价于求与数据行为分布KL散度最小的策略参数\theta:
\qquad L=-E_{(s,a)\sim p_{data}}(log(\pi_{\theta}(a|s)))
虽然behavior cloning和IRL都是目标为最大化数据行为的概率似然,然而它们建立的模型不同:BC直接对策略建模,而IRL利用soft optimal模型对reward进行建模,然后通过inference来得到策略。因此IRL的好处在于估计出了每步的reward,那么导出的策略会尽力最大化整条路径的reward和,能避免behavior cloning中的偏差问题p_{data}(o_t)=p_{\pi_{\theta}}(o_t)。
而将会看到behavior cloning和IRL区别其实可以认为是普通auto-encoder和GAN的区别,GAN的D构建了能有复杂表示的目标(因此实验结果GAN优于其他方法),IRL的reward起到了一样的作用。
与GAN的联系
对于接触过GAN的,上面过程十分像对抗学习过程,reward与policy的对抗:

reward网络就是discriminator,而policy网络就是generator。
《Guided Cost Learning》 ICML 2016
对于(标准GAN)discriminator的更新公式为:
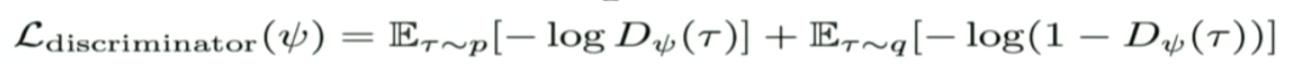
因为最优分类器为:
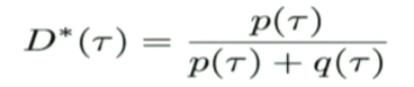
那么在IRL中我们假设D有如下参数化形式:
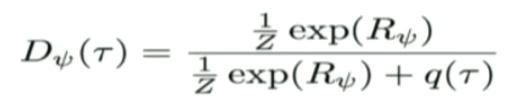
其中\frac{1}{Z}exp(R_{\psi})代表真实数据的概率分布,q(\tau)为policy网络的分布。
将上式代入L_{discriminator}就得到IRL中的reward更新公式。
接下来看generator/policy网络的更新过程:
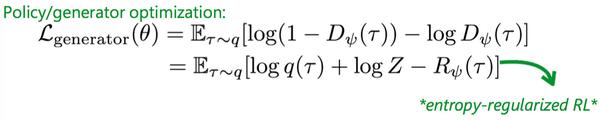
上一等式是generator网络的更新目标,而使用IRL的参数化形式后可以得到下一等式,就是policy网络目标。
Generative Adversarial Imitation Learning Ho & Ermon, NIPS 2016
但是在这篇paper中直接采用了更直接的GAN(而非之前较复杂的参数化形式)来训练IRL:discriminator就是使用标准GAN的D,即是个classifier对真实或生成样本输出(其是真实的)概率值,然后把D的log值作为reward值来训练policy:

而这种更简单的形式在许多任务中取得了不错的结果:(然而原paper的论证过程绝不"简单",我也还没完全读懂)
总结:
soft optimal model
第一部分我们从解释人类的行为出发,人类行为suboptimal,有随机性,因此不能用之前的最优策略目标来解释。为此我们引入了一种特殊的概率图,称为soft optimal model,其中包含optimality变量p(\mathcal{O_t}|s_t,a_t)\varpropto exp(r(s_t,a_t))携带了概率形式的reward信息。
之后采用了概率图的inference方法来推导

其中发现后向信息等价于值函数:Q(s_t,a_t)=\log\beta_t(s_t,a_t),由于是soft optimal model,因此Q-value更新也是soft max的:V(s_t)=\log E_{a_t}[exp(Q(s_t,a_t))]。
第二点利用推断算法来计算策略\pi(a|s),说明了inference=planning(在这个soft optimal model进行推断就等价于找到soft optimal的策略),而且发现了soft Q-learning算法,其策略为Boltzmann explorationexp(Q(s,a)-V(s))。以及soft policy gradient算法,即目标函数加入entropy项。
这种soft optimal的算法有多种好处
1.增加exploration 2. 更易于被finetune成更加specific的任务 3.打破瓶颈,避免suboptimal。4.更好的robustness 5.能model人的动作
Inverse RL
当只有人类的数据(suboptimal,有随机性)时,我们思路是用soft optimal model来学习出reward函数,那么根据soft optimal model来以最大数据的概率似然为目标,

由此直接推导出MaxEnt算法,但是为了应用到大状态空间中,将第二项用任一max-ent RL在当前reward下学到的策略样本路径来估计。
最后讨论了IRL与GAN的相似性:
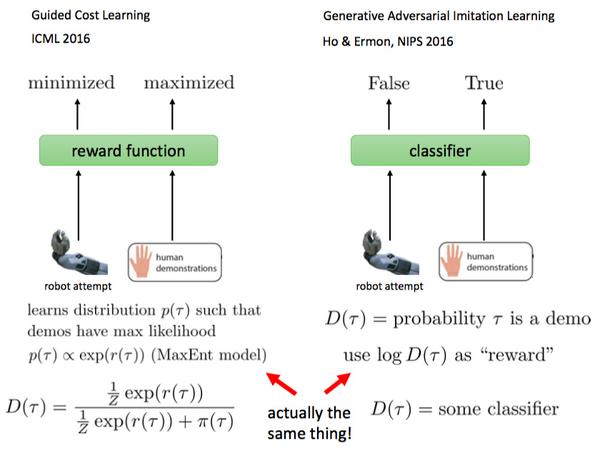
GAN的D可以被reward值参数化,来建立完全一致的联系。但是也可以更简单的,作为标准GAN来应用到IRL中,只是reward用log D替代。
附录:
对于这个模型的利用采用概率图的推断算法,而有三种推断情形:

接下来将仔细解释这三种推断情形。
后向信息Backward messages
已知当前情形和动作s_t,a_t,那之后都想要达到最优的概率\beta_t(s_t,a_t)=p(\mathcal{O_{t:T}}|s_t,a_t)

其中离散情形时,积分换成求和即可。最后一项中p(s_{t+1}|s_t,a_t)是环境转移概率,p(\mathcal{O_t}|s_t,a_t)\varpropto exp(r(s_t,a_t))之前说了,现在要处理p(\mathcal{O_{t+1:T}}|s_{t+1})这项,而且我们记它为\beta_{t+1}(s_{t+1}):
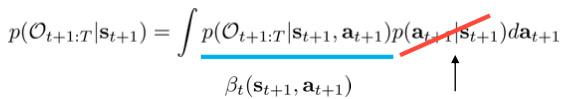
我们把p(a_{t+1}|s_{t+1})认为是先验分布,常为均匀分布(对于不均匀分布情况,\log p(a_t|s_t)可以被添加到r(s_t,a_t)中,因此均匀分布假设容易被推广,不细讲了)。
上述计算过程可以归结为下述循环,循环结束后每步的\beta_t(s_t,a_t)就都知道了:
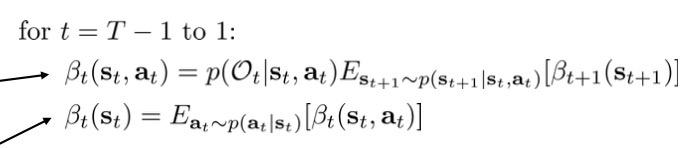
由于这个循环过程从T-1到1,所以信息是向后传播的。
后向信息与Q-learning的联系
(由于\mathcal{O}发生概率与reward成正比,那么想要之后的\mathcal{O_{t:T}}发生概率大的话,那就需要之后的reward大,因此\beta可以接受到后面的reward信息来对当前s_t,a_t进行衡量,这点就自然和Q-value联系起来)
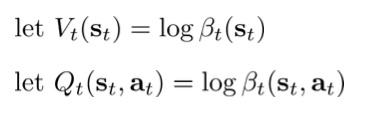
代入循环的第二步:\large\beta_t(s_t)=E_{a_t\sim p(a_t|s_t)}[\beta_t(s_t,a_t)],那么
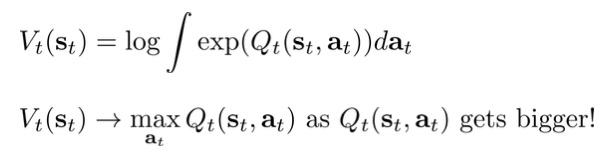
可以看到如果最大的Q(s_t,a_t)和其他的Q相比十分大时,那V(s_t)=\max_{a_t}Q(s_t,a_t)(Q-learning的第二步),因此V(s_t)=\log E_{a_t}[exp(Q(s_t,a_t))]是一种soft max(不要和softmax搞混了)。
与Q-learning比较:

也就是把第二步的max改为一种soft max,而将会看到这个改动对应于soft optimality的策略。
需要说明的是在循环的第一步中:

使用Q(s_t,a_t)=r(s_t,a_t)+\log E_{s_{t+1}}[exp(V(s_{t+1}))]不好用,而用Q-learning对Q-Value更新更好,所以Q-learning第一步不需要改进。
因此后向信息其实可以理解为能量为值函数的能量函数,这点对应于p(\mathcal{O_t}|s_t,a_t)是以当前reward为能量的能量函数。
Policy computation
我们最为关心的一点是根据这个模型导出的最优策略应该是怎样的,即计算\pi(a_t|s_t)=p(a_t|s_t,\mathcal{O}_{1:T}):
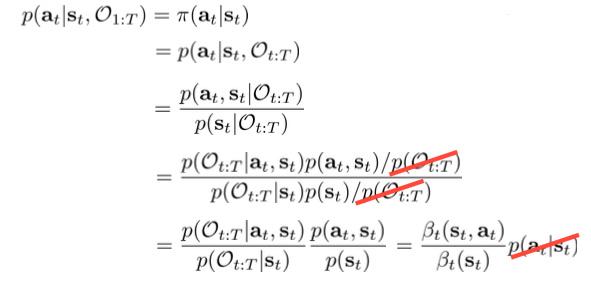
因此这个模型导出的最优策略与Q值的exp成正比,是一种随机策略,而非Q-learning的greedy或\epsilon-greedy策略。
更进一步我们可以加上discount项\gamma,以及temperature参数\alpha(加上这个参数,等价于把reward调小\alpha倍,而\alpha\to0时,那soft max退化为max,可以控制策略的exploration程度):
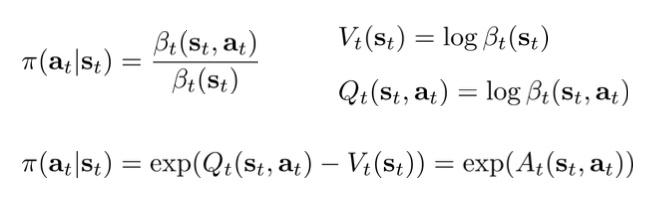
因此这个模型导出的最优策略与Q值的exp成正比,是一种随机策略,而非Q-learning的greedy或\epsilon-greedy策略。
更进一步我们可以加上discount项\gamma,以及temperature参数\alpha(加上这个参数,等价于把reward调小\alpha倍,而\alpha\to0时,那soft max退化为max,可以控制策略的exploration程度):
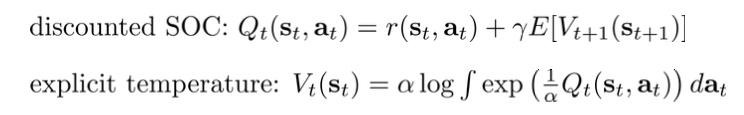
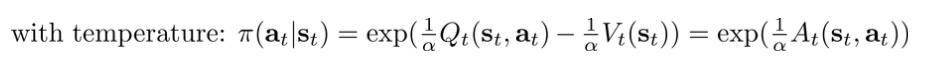
可以看出这个就是Boltzmann exploration。
Forward messages
接下来想要知道p(s_t|\mathcal{O}_{1:t-1}),即如果我每一步都是想要最优的,那么我t时刻会在哪里:
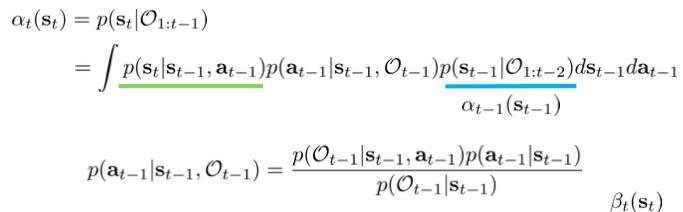
这个计算过程没有什么好讲的地方。
而更重要的问题是p(s_t|\mathcal{O}_{1:T})也就是说我从头到尾每一步都要是最优的,那么我的状态分布应该是怎样的
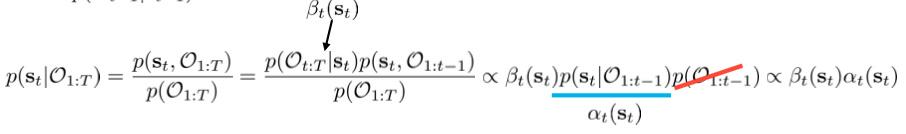
也就是前向信息与后向信息相乘,这个和概率图的置信信息校准一样,那么得到的就是状态的边缘分布:
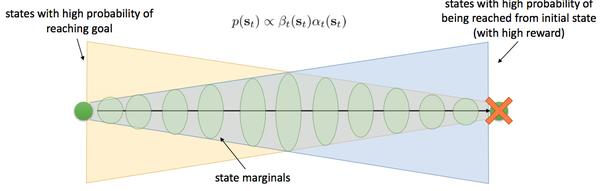
蓝色分布代表前向信息p(s_t|\mathcal{O}_{1:t-1}),黄色代表后向信息p(\mathcal{O_{t:T}}|s_{t}),而绿色区域就代表每一步都要是最优的轨迹分布。


