从 SGD 到 Adam —— 深度学习优化算法概览(一)

潜水半退乎

楔子

前些日在写计算数学课的期末读书报告，我选择的主题是「分析深度学习中的各个优化算法」。在此前的工作中，自己通常就是无脑「Adam 大法好」，而对算法本身的内涵不知所以然。一直希望能抽时间系统的过一遍优化算法的发展历程，直观了解各个算法的长处和短处。这次正好借着作业的机会，补一补课。

本文主要借鉴了 @Juliuszh 的文章[1]思路，使用一个 general 的框架来描述各个梯度下降变种算法。实际上，本文可以视作对[1]的重述，在此基础上，对原文描述不够详尽的部分做了一定补充，并修正了其中许多错误的表述和公式。

另一主要参考文章是 Sebastian Ruder 的综述[2]。该文十分有名，大概是深度学习优化算法综述中质量最好的一篇了。建议大家可以直接阅读原文。本文许多结论和插图引自该综述。

对优化算法进行分析和比较的文章已有太多，本文实在只能算得上是重复造轮，旨在个人学习和总结。希望对优化算法有深入了解的同学可以直接查阅文末的参考文献。

引言

最优化问题是计算数学中最为重要的研究方向之一。而在深度学习领域，优化算法的选择也是一个模型的重中之重。即使在数据集和模型架构完全相同的情况下，采用不同的优化算法，也很可能导致截然不同的训练效果。

梯度下降是目前神经网络中使用最为广泛的优化算法之一。为了弥补朴素梯度下降的种种缺陷，研究者们发明了一系列变种算法，从最初的 SGD (随机梯度下降) 逐步演进到 NAdam。然而，许多学术界最为前沿的文章中，都并没有一味使用 Adam/NAdam 等公认“好用”的自适应算法，很多甚至还选择了最为初级的 SGD 或者 SGD with Momentum 等。

本文旨在梳理深度学习优化算法的发展历程，并在一个更加概括的框架之下，对优化算法做出分析和对比。

Gradient Descent

梯度下降是指，在给定待优化的模型参数 \theta \in \mathbb{R}^d 和目标函数 J(\theta) 后，算法通过沿梯度 \nabla_\theta J(\theta) 的相反方向更新 \theta 来最小化 J(\theta) 。学习率 \eta 决定了每一时刻的更新步长。对于每一个时刻 t ，我们可以用下述步骤描述梯度下降的流程：

(1) 计算目标函数关于参数的梯度

g_t = \nabla_\theta J(\theta)

(2) 根据历史梯度计算一阶和二阶动量

m_t = \phi(g_1, g_2, \cdots, g_t)

v_t = \psi(g_1, g_2, \cdots, g_t)

(3) 更新模型参数

\theta_{t+1} = \theta_t - \frac{1}{\sqrt{v_t + \epsilon}} m_t

其中， \epsilon 为平滑项，防止分母为零，通常取 1e-8。

Gradient Descent 和其算法变种

根据以上框架，我们来分析和比较梯度下降的各变种算法。

Vanilla SGD

朴素 SGD (Stochastic Gradient Descent) 最为简单，没有动量的概念，即

m_t = \eta g_t

v_t = I^2

\epsilon = 0

这时，更新步骤就是最简单的

\theta_{i+1}= \theta_t - \eta g_t

SGD 的缺点在于收敛速度慢，可能在鞍点处震荡。并且，如何合理的选择学习率是 SGD 的一大难点。

Momentum

SGD 在遇到沟壑时容易陷入震荡。为此，可以为其引入动量 Momentum[3]，加速 SGD 在正确方向的下降并抑制震荡。

m_t = \gamma m_{t-1} + \eta g_t

SGD-M 在原步长之上，增加了与上一时刻步长相关的 \gamma m_{t-1} ，\gamma 通常取 0.9 左右。这意味着参数更新方向不仅由当前的梯度决定，也与此前累积的下降方向有关。这使得参数中那些梯度方向变化不大的维度可以加速更新，并减少梯度方向变化较大的维度上的更新幅度。由此产生了加速收敛和减小震荡的效果。

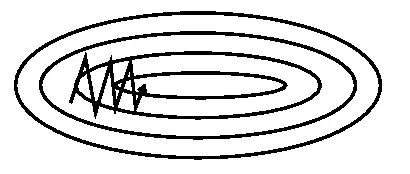
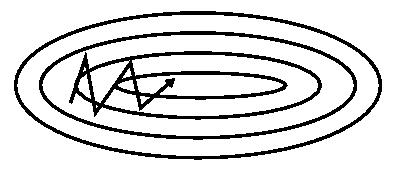
从图 1 中可以看出，引入动量有效的加速了梯度下降收敛过程。

Nesterov Accelerated Gradient

更进一步的，人们希望下降的过程更加智能：算法能够在目标函数有增高趋势之前，减缓更新速率。

NAG 即是为此而设计的，其在 SGD-M 的基础上进一步改进了步骤 1 中的梯度计算公式：

g_t = \nabla_\theta J(\theta - \gamma m_{t-1})

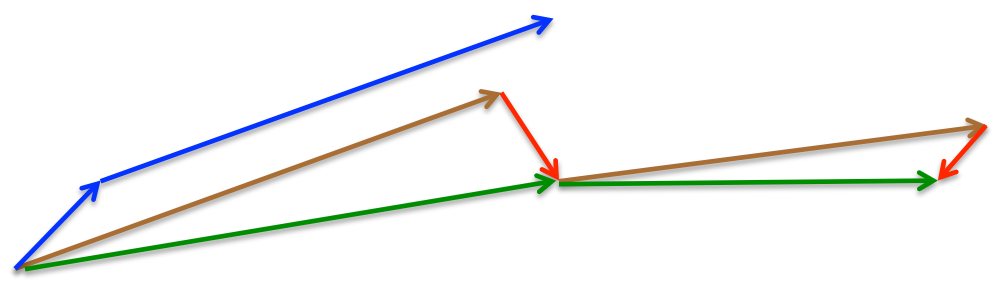
参考图 2，SGD-M 的步长计算了当前梯度（短蓝向量）和动量项（长蓝向量）。然而，既然已经利用了动量项来更新，那不妨先计算出下一时刻 \theta 的近似位置（棕向量），并根据该未来位置计算梯度（红向量），然后使用和 SGD-M 中相同的方式计算步长（绿向量）。这种计算梯度的方式可以使算法更好的「预测未来」，提前调整更新速率。

Adagrad

SGD、SGD-M 和 NAG 均是以相同的学习率去更新 \theta 的各个分量。而深度学习模型中往往涉及大量的参数，不同参数的更新频率往往有所区别。对于更新不频繁的参数（典型例子：更新 word embedding 中的低频词），我们希望单次步长更大，多学习一些知识；对于更新频繁的参数，我们则希望步长较小，使得学习到的参数更稳定，不至于被单个样本影响太多。

Adagrad[4] 算法即可达到此效果。其引入了二阶动量：

v_t = \text{diag}(\sum_{i=1}^t g_{i,1}^2, \sum_{i=1}^t g_{i,2}^2, \cdots, \sum_{i=1}^t g_{i,d}^2)

其中， v_t \in \mathbb{R}^{d\times d} 是对角矩阵，其元素 v_{t, ii} 为参数第 i 维从初始时刻到时刻 t 的梯度平方和。

此时，可以这样理解：学习率等效为 \eta / \sqrt{v_t + \epsilon} 。对于此前频繁更新过的参数，其二阶动量的对应分量较大，学习率就较小。这一方法在稀疏数据的场景下表现很好。

RMSprop

在 Adagrad 中， v_t 是单调递增的，使得学习率逐渐递减至 0，可能导致训练过程提前结束。为了改进这一缺点，可以考虑在计算二阶动量时不累积全部历史梯度，而只关注最近某一时间窗口内的下降梯度。根据此思想有了 RMSprop[5]。记 g_t \odot g_t 为 g_t^2 ，有

v_t = \gamma v_{t-1} + (1-\gamma) \cdot \text{diag}(g_t^2)

其二阶动量采用指数移动平均公式计算，这样即可避免二阶动量持续累积的问题。和 SGD-M 中的参数类似，\gamma 通常取 0.9 左右。

Adadelta

待补充

Adam

Adam[6] 可以认为是 RMSprop 和 Momentum 的结合。和 RMSprop 对二阶动量使用指数移动平均类似，Adam 中对一阶动量也是用指数移动平均计算。

m_t = \eta[ \beta_1 m_{t-1} + (1 - \beta_1)g_t ]

v_t = \beta_2 v_{t-1} + (1-\beta_2) \cdot \text{diag}(g_t^2)

其中，初值

m_0 = 0

v_0 = 0

注意到，在迭代初始阶段，m_t 和 v_t 有一个向初值的偏移（过多的偏向了 0）。因此，可以对一阶和二阶动量做偏置校正 (bias correction)，

\hat{m}_t = \frac{m_t}{1-\beta_1^t}

\hat{v}_t = \frac{v_t}{1-\beta_2^t}

再进行更新，

\theta_{t+1} = \theta_t - \frac{1}{\sqrt{\hat{v}_t} + \epsilon } \hat{m}_t

可以保证迭代较为平稳。

NAdam

NAdam[7] 在 Adam 之上融合了 NAG 的思想。

首先回顾 NAG 的公式，

g_t = \nabla_\theta J(\theta_t - \gamma m_{t-1})

m_t = \gamma m_{t-1} + \eta g_t

\theta_{t+1} = \theta_t - m_t

NAG 的核心在于，计算梯度时使用了「未来位置」\theta_t - \gamma m_{t-1}。NAdam 中提出了一种公式变形的思路[7]，大意可以这样理解：只要能在梯度计算中考虑到「未来因素」，即能达到 Nesterov 的效果；既然如此，那么在计算梯度时，可以仍然使用原始公式 g_t = \nabla_\theta J(\theta_t) ，但在前一次迭代计算 \theta_t 时，就使用了未来时刻的动量，即 \theta_t = \theta_{t-1} - m_t ，那么理论上所达到的效果是类似的。

这时，公式修改为，

g_t = \nabla_\theta J(\theta_t)

m_t = \gamma m_{t-1} + \eta g_t

\bar{m}_t = \gamma m_t + \eta g_t

\theta_{t+1} = \theta_t - \bar{m}_t

理论上，下一刻的动量为 m_{t+1} = \gamma m_t + \eta g_{t+1}，在假定连续两次的梯度变化不大的情况下，即 g_{t+1} \approx g_t，有 m_{t+1} \approx \gamma m_t + \eta g_t \equiv \bar{m}_t。此时，即可用 \bar{m}_t 近似表示未来动量加入到 \theta 的迭代式中。

类似的，在 Adam 可以加入 \bar{m}_t \leftarrow \hat{m}_t 的变形，将 \hat{m}_t 展开有

\hat{m}_t = \frac{m_t}{1-\beta_1^t} = \eta[ \frac{\beta_1 m_{t-1}}{1-\beta_1^t} + \frac{(1 - \beta_1)g_t}{1-\beta_1^t} ]

引入

\bar{m}_t = \eta[ \frac{\beta_1 m_{t}}{1-\beta_1^{t+1}} + \frac{(1 - \beta_1)g_t}{1-\beta_1^t} ]

再进行更新，

\theta_{t+1} = \theta_t - \frac{1}{\sqrt{\hat{v}_t} + \epsilon } \bar{m}_t

即可在 Adam 中引入 Nesterov 加速效果。

可视化分析

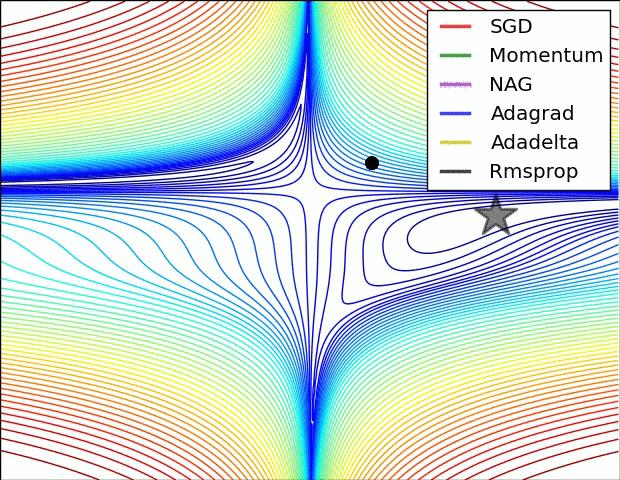
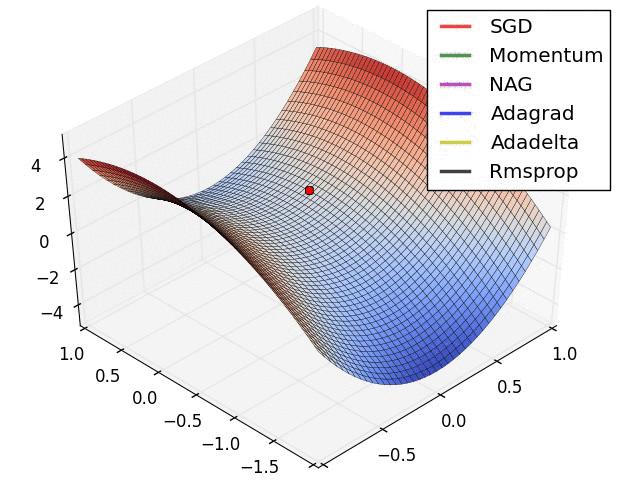
图 3: SGD optimization on loss surface contours

图 3 和图 4 两张动图直观的展现了不同算法的性能。(Image credit: Alec Radford)

图 3 中，我们可以看到不同算法在损失面等高线图中的学习过程，它们均同同一点出发，但沿着不同路径达到最小值点。其中 Adagrad、Adadelta、RMSprop 从最开始就找到了正确的方向并快速收敛；SGD 找到了正确方向但收敛速度很慢；SGD-M 和 NAG 最初都偏离了航道，但也能最终纠正到正确方向，SGD-M 偏离的惯性比 NAG 更大。

图 4 展现了不同算法在鞍点处的表现。这里，SGD、SGD-M、NAG 都受到了鞍点的严重影响，尽管后两者最终还是逃离了鞍点；而 Adagrad、RMSprop、Adadelta 都很快找到了正确的方向。

关于两图的讨论，也可参考[2]和[8]。

可以看到，几种自适应算法在这些场景下都展现了更好的性能。