范畴论学习笔记16：函子范畴、范畴的等价

Arjuna

语言学话题下的优秀答主

目录：类型论驿站写作计划

前一篇：范畴论学习笔记15：自然变换

后一篇：范畴论学习笔记17：米田引理

学习材料：Category Theory: A Gentle Introduction - Logic Matters，最近更新（2018年1月29日）的版本。这份笔记对应的是第 22-23 章。

圏論勉強１６：関手圏

函子范畴/関手圏（functor category）

定义102

从 \mathscr{C} 到 \mathscr{D} 的函子范畴，记为 [\mathscr{C,D}] ，是以所有的协变函子 F:\mathscr{C\to D} 为对象，以函子之间的自然变换为箭头的范畴。

逆变函子组成的范畴记为 [\mathscr{C^{op}\to D}] 。

离散范畴 \bar{2} 只有两个对象： \bullet 和 \star ，以及它们各自的恒等箭头（此前笔记中我一直将identity arrow 翻译成“单位箭头”，现改译为恒等箭头） 1_\bullet, 1_\star 。函子范畴 [\bar{2},\mathscr{C}] 的数据是什么呢？

它的对象是函子 F:\bar{2}\to \mathscr{C} ，和一对 \mathscr{C} 对象 (X,Y) 之间存在双射；平行函子 F,F' 之间的自然变换就是它的箭头，就是任何一对 \mathscr{C} 箭头 (j:X\to X',k:Y\to Y') 。因此，该函子箭头本质上就是积范畴 \mathscr{C\times C} ，或更严格地说，和这个积范畴是同构的。

回忆初等数学里， x^2 = x\times x 。

定理108

函子范畴 [\mathscr{C,D}] 中的同构就是自然变换 \psi:F\Rightarrow G ，其中 \mathscr{C}\Rightarrow_{G}^{F}\mathscr{D} 。

从函子范畴构建的 hom-函子

定义103

我们用 Nat(F,G) 来指代从 F 到 G 的自然变换的集合，如果这样的自然变换存在的话。

定义104

我们用 Nat(-,G) 来指代逆变 hom-函子 [\mathscr{C,D}](-,G):[\mathscr{C,D}]\to \sf Set ；用 Nat(F,-) 来指代同变 hom-函子 [\mathscr{C,D}](F,-) 。

赋值和对角函子

定义105

函子 ev_A:[\mathscr{C,D}]\to\mathscr{D} 将函子 F:\mathscr{C\to D} 映射到 FA 上，将自然变换 \alpha :F\Rightarrow G 映射到 \alpha_A:FA\to GA 上。

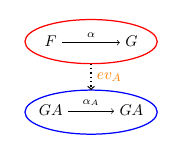
回顾函子（F10）：

设 \mathscr{C,D} 为非空范畴， D 是任意 \mathscr{D} 对象。那么存在一个对应的“坍塌至 D ”的常函子 \Delta_D:\mathscr{C\to D} ，将所有的 \mathscr{C} 对象都映射到 D ，将所有的 \mathscr{C} 箭头都映射到 1_D 。

定义106

函子 \Delta_\textsf{J}:\mathscr{C}\to[\textsf{J},\mathscr{C}] 将一个对象 C 映射到函子 \Delta_C:\textsf{J}\to \mathscr{C} 上，将箭头 f:C\to C' 映射到从 \Delta_C 到 \Delta_C' 的自然变换上，自然变换的每一个构件又都是 f 。

参考 F10 的定义，将上面的左图加以归约，就可以得到右图。所以我们可以确信上述自然变换的每一个构件也都是 f 。
逗号范畴 (\Delta_\textsf{J}\downarrow D) 正是 D 上的锥范畴。于是，我们可认为 D 上的一个锥就是逗号范畴 (\Delta_\textsf{J}\downarrow D) 中的一个对象，而一个极限锥就是这个范畴里的终对象。

作为自然变换的椎体

让我们关注一个小范畴 \textbf{J} 。考虑函子 [\textbf{J},\mathscr{C}] ，其对象为“作为函子的范畴图” D:\textbf{J}\to \mathscr{C} ，其箭头为这些函子之间的自然变换。

[\textbf{J},\mathscr{C}] 中一种特殊的对象是诸如 \Delta_C:\textbf{J}\to \mathscr{C} 的常函子，即将所有的 \textbf{J} 对象都映射到 C ，将每一个 \textbf{J} 箭头都映射到 1_C 的函子范畴图。

那么从 \Delta_C 到另一个函子范畴图 D 的自然变换是什么呢？这个自然变换就是一组用 J\in \textbf{J} 做指数（index）的 \textbf{J} 箭头 \alpha_J:\Delta_C(J)\to D(J) ，也就是箭头 \alpha_J:C\to D(J) ，使得对于每一个 \textbf{J} 中的 d:K\to L ，下面的正方形在 \mathscr{C} 中都是可交换的，相应的三角形也是（平凡）可交换的。

这个三角形就是 C 加上 \alpha_J 构成的一个在 D 上的椎体（的一个侧面）。反之，椎体也构成了自然变换 \alpha:\Delta_C\Rightarrow D 。

定理109

在 D:\textbf{J}\to \mathscr{C} 上的一个以 C 为顶点（vertex）的椎体包含 C 和一个从平凡函子 \Delta_C:J\to\mathscr{C} 到 D 的自然变换。

极限函子（limit functors）

定义107

假设每一个形状为 \sf J 的范畴图 D 都在 \mathscr{C} 中有一个极限，那么函子 \lim_{\leftarrow \textsf{J}}:[\textsf{J},\mathscr{C}]\to\mathscr{C}

将 [\textsf{J},\mathscr{C}] 对象 D 发送到（在 D 上选取的一个极限锥 [\lim D,\pi_J] ）的顶点 \lim D 上。
将 [\textsf{J},\mathscr{C}] 箭头 \alpha :D\Rightarrow D' 发送到满足“对于所有 \sf J 中的 J ， \pi_J'\circ u_\alpha = \alpha_J\circ \pi_J ”的箭头 u_\alpha:\lim D\to \lim D' 上。

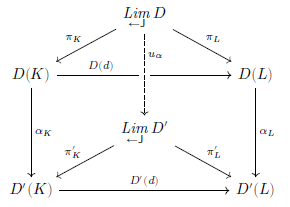
定理110

假设上图相关的形状的极限是存在的，那么，如果我们有一个自然同构 D\cong D' ，则有 \lim D\cong \lim D' 。

定理111

假设 \mathscr{C} 拥有所有形如 \sf J 的极限，那么对于函子 F:\mathscr{C\to D} 保存的每一个 D:\textsf{J}\to \mathscr{C} ， F(\lim_{\leftarrow \textsf{J}}D)\cong \lim_{\leftarrow \textsf{J}}(F\circ D) 。简而言之： F 和 \lim_{\leftarrow \textsf{J}} 可交换。

定义108

对于所有小范畴 \textsf{J} ，和形状为 \textsf{J} 的极限可交换的函子，是连续（continuous）的。

范畴的等价是比“上至同构”更弱的一种关系。

定义109

范畴 \mathscr{C} 和 \mathscr{D} 是等价（equivalent）的，记为 \mathscr{C}\simeq \mathscr{D} ，当且仅当存在函子 F:\mathscr{C\to D}, F:\mathscr{D\to C} ，以及一对自然同构 \alpha:1_\mathscr{C}\Rightarrow GF; \beta:FG\Rightarrow 1_\mathscr{D} 。

定义113

假定一个足够强的选择原则（a sufficiently strong choice principle），函子 F:\mathscr{C\to D} 是 \mathscr{C} 和 \mathscr{D} 的等价的一部分，当且仅当 F 是忠实（faithful）、全乎（full）和对于对象是本质满射（essentially surjective on objects）。

感谢 @爱笑的马叔老师转述的一个关于范畴等价的形象说法：

范畴等价的刻画是全乎，忠实，稠密。Baez-Baertles-Dolan给了一个“形象”描述。
如若一个函子不全乎，则它忘却了结构。 如若不忠实，则它忘却了填料（stuff）。 如若不稠密，则它忘却了性质。 https://ncatlab.org/nlab/show/stuff%2C+structure%2C+property

其中稠密（dense）是本质满射的另一种说法。

另外，南京师范大学贺伟老师在其所著的《范畴论》中，将 faithful 翻译为“局部单”（针对函子）；将 full 翻译为“局部满”（针对函子）。我将 faithful 简单地翻译成“忠实”，将“full”简单地翻译成“全[乎]”，为了把修饰子范畴的 full （满）相区别。

定理112

Set 和 Pfn 不是同构的。

定理114

\sf Pfn\simeq Set .

定理115

\sf FinOrdn\simeq FinSet . 其中 FinOrdn 是包含空集和所有形如 \{0,1,2,\dots,n-1\} 的集合以及它们之间的函数的 FinSet 的全乎子范畴。

骨架和邪灵（skeletons and evil）

定义110

范畴 \mathscr{C} 被称为范畴 \mathscr{C} 的骨架（skeleton，或译为骸骨），如果 \mathscr{S} 是 \mathscr{C} 的一个满子范畴，且只包含每个 \mathscr{C} 中的同态对象类（class of isomorphic objects）中的一个对象。如果一个范畴是另一个范畴的骨架，我们称这个范畴是骨架范畴（skeletal）。

定理116

如果果 \mathscr{S} 是 \mathscr{C} 的一个骨架，那么 \mathscr{S\simeq C} 。