embedding层如何反向传播
embedding层本质是矩阵乘
可能大家一看到这个题目第一反应是:这不很显然么?反向传播怎么传播就怎么传播,概莫能外。但仔细一想,也不是那么简单。在端到端的训练中,embedding层是把one-hot编码的categorial feature稠密化成一个实数向量后的产物,整体看起来,有点像mlp的源头输入。反向传播其实是求各种weight的变化对最终的误差能造成什么样的影响,或者说是各种weight怎么调整能让预估误差尽可能小,其实就是给各种weight找到梯度下降最快的方向,让损失函数快速地全局达到一个最优点。如果把embedding层看做输入,应用反向传播的概念就有点问题,因为这里没有weight什么事情。
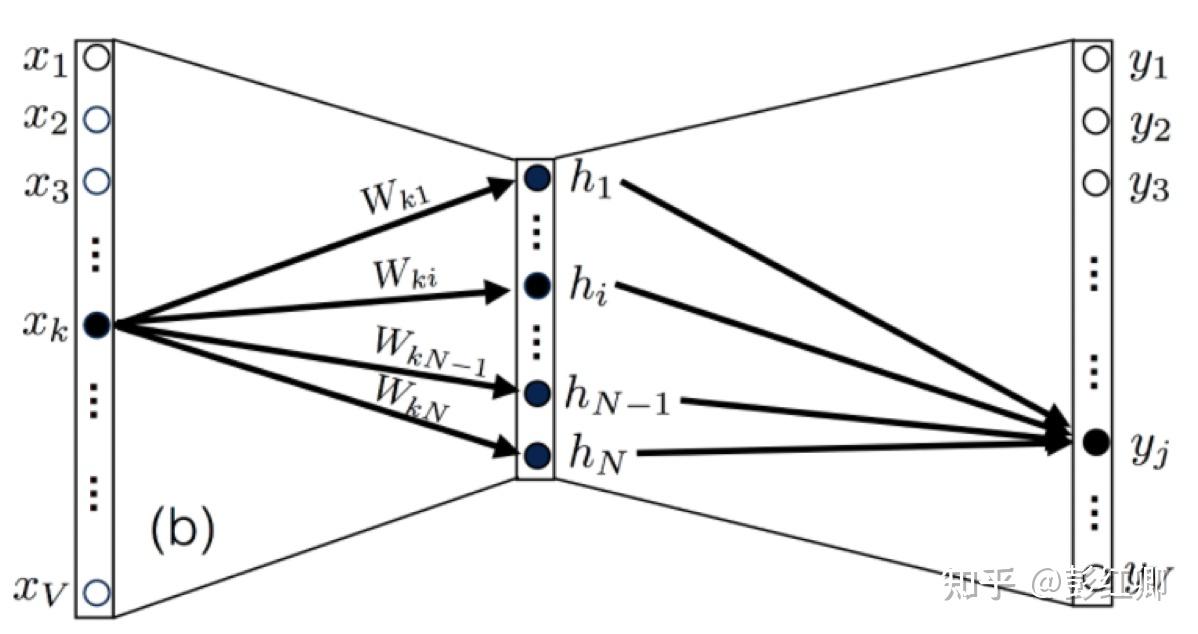
但其实embedding就是weight本身,只是没那么明显。下面这个图虽然借鉴word2vec,但作为embedding layer的示意图也能说明问题,从X到隐层H,就是一个embedding lookup的过程,也是一个one-hot编码后的X跟输入矩阵的乘积。但是这里注意跟Word2vec一样,隐层之后是没有激活函数的,这个隐层其实叫linear layer。把这个图扩展开来,多个X的隐层向量concat起来,隐层就成了MLP的输入层,Y就是MLP的第一层。
import tensorflow as tf
import numpy as np
NUM_CATEGORIES, EMBEDDING_SIZE = 5, 3
y = tf.placeholder(name='class_idx', shape=(1,), dtype=tf.int32)
RS = np.random.RandomState(42)
W_em_init = RS.randn(NUM_CATEGORIES, EMBEDDING_SIZE)
W_em = tf.get_variable(name='W_em',
initializer=tf.constant_initializer(W_em_init),
shape=(NUM_CATEGORIES, EMBEDDING_SIZE))
# Using tf.nn.embedding_lookup
y_em_1 = tf.nn.embedding_lookup(W_em, y)
# Using multiplication
y_one_hot = tf.one_hot(y, depth=NUM_CATEGORIES)
y_em_2 = tf.matmul(y_one_hot, W_em)
sess = tf.InteractiveSession()
sess.run(tf.global_variables_initializer())
sess.run([y_em_1, y_em_2], feed_dict={y: [1.0]})
# [array([[ 1.5230298 , -0.23415338, -0.23413695]], dtype=float32),
# array([[ 1.5230298 , -0.23415338, -0.23413695]], dtype=float32)]上面是从代码的角度去理解embedding_lookup本质是矩阵乘的事实
如何反向传播
f(x)=f_{2}(sigmoid((f_{1}(x))W_{2}+B_{2}) , f_{1}(x)=XW_{emb}W_{1}+B_{1} ,假定MLP拟合的函数如f(x),其中X是one-hot编码的特征输入, XW_{emb} 是MLP的输入层,linear layer的部分体现在 (XW_{emb})W_{1} ,即两个矩阵直接乘了,没有激活函数,没有non-linear的处理。sigmoid((XW_{emb})W_{1}+B_{1}) 是MLP第一层(上图中的Y)中的神经元节点的值,也是MLP第二层的输入, f_{2}(...) 是第二层往后MLP拟合的函数。从公式可以看出,对 W_{1} 求偏导,留下 (XW_{emb}) (即embedding lookup后得到的embedding,注意对 W_{1} 求导的时候,输入是embedding层,看不到X),对 W_{emb} 求偏导则留下X和 W_{1} 。
\frac{\partial_{loss}}{\partial_{W_{emb}}}=\frac{\partial_{L}}{\partial_{f}}*\frac{\partial_{f}}{\partial_{W_{emb}}}=\frac{\partial_{L}}{\partial_{f}}*\frac{\partial_{f}}{\partial_{f_{2}}}*\frac{\partial_{f_{2}}}{\partial_{W_{emb}}}=\frac{\partial_{L}}{\partial_{f}}*\frac{\partial_{f}}{\partial_{f_{2}}}*\frac{\partial_{f_{2}}}{\partial_{f_{1}}}*\frac{\partial_{f_{1}}}{\partial_{W_{emb}}}
(注意一个embedding乘以W1以后对多个前向通路产生了作用,反向传播的时候W1也是有多个通路会把误差反向传递,因此也构成了一个hessian矩阵)
具体的推导请参考https://web.eecs.umich.edu/~justincj/teaching/eecs442/notes/linear-backprop.html

注意,此文中的X相当于本文图中和前文的 W_{emb} ,而W则相当于隐层跟输出Y之间的矩阵 W_{1} ,Y相当于MLP第一层的神经元输入。换成本文的指代就是这样:
\frac{\partial_{L}}{\partial_{W_{emb}}}=\frac{\partial_{L}}{\partial_{Y}}W^{\mathsf{T}} , \frac{\partial_{L}}{\partial_{W_{1}}}=W_{emb}^{\mathsf{T}}\frac{\partial_{L}}{\partial_{Y}}

