模糊搜索&自动纠错——Fuzzy Query by Levenshtein Automata

在我们每天使用的搜索引擎中，有这么一个简单的小功能经常被忽略——模糊搜索以及自动纠错。当我们输入一个错误的单词时，与其相似的结果将会被返回。这个小功能需要很高的效率以提供良好的用户体验。

举个栗子：

不知道你有没有思考过这是如何实现的呢？

如果你对它感兴趣的话，请耐心读完本文，你将会有所收获。

本文的目的在于以简单易懂的方式阐述一种实现Fuzzy Query的方法——Levenshtein Automata。这种方法目前被用于Apache Lucene里。

在我们开始聊看起来很复杂的Levenshtein Automata前，首先需要知道以下这些事情。

Levenshtein Distance

首先，模糊匹配返回的单词集合是与搜索的单词相似的结果。那么，我们首先需要的就是定义这种相似。

给定两个字符串（单词），称两个字符串之间的“距离”为Levenshtein Distance，即编辑距离。简单来说，就是由字符串A变成字符串B所需要的最少变化（插入，删除，替换）次数。

示例：abcd 和 acdf 的编辑距离为2。
abcd ------> 删除 b ------> acd
acd ------> 插入 f ------> acdf

编辑距离的定义非常简单，距离越小的两个单词就越相似。接下来，对于给定的两个字符串，我们需要用一种方法来计算编辑距离。直观的方法是递归，更优的方法是动态规划。在这里不详细介绍了，这个问题是个经典算法问题，有太多的资料可以去看。

这里贴一下Lucene内的实现。对于利用动态规划编辑距离的计算，算法时间复杂度为 O(MN) ，空间复杂度可以优化到 O(N) 。

说到这里，我们已经知道如何定义相似。回到文章开始的使用场景，我们可以把这个问题简单提炼一下。

问题的输入：

已知的词典集合D，D中包含着大量的正确单词。
用户输入查询的字符串query。
距离n，衡量某一字符串与查询query的相似程度（即编辑距离大小）

问题的输出：

一个集合results，是与query距离小于n的，词典D的子集。

Naive Method

说到这里，想必你已经想出来一个最简单的方法了——把集合D中每一个单词和query的距离都计算一下，返回结果小于n的就可以了。

然而，这种方法每作一次查询都需要遍历一次词典D，并计算每个单词与query的编辑距离，在上述需要立即给用户返回结果的场景中，显然不具有现实意义。我们需要更高效的方法。

下面就要提到本文的主角了——Levenshtein Automata。

Levenshtein Automata

简单来说，这个算法是对给定的query和距离n建立一个有限状态自动机FSA（Finite State Automaton），这样就可以在 O(N) 时间内判断两个字符串是否相似（编辑距离小于n）。

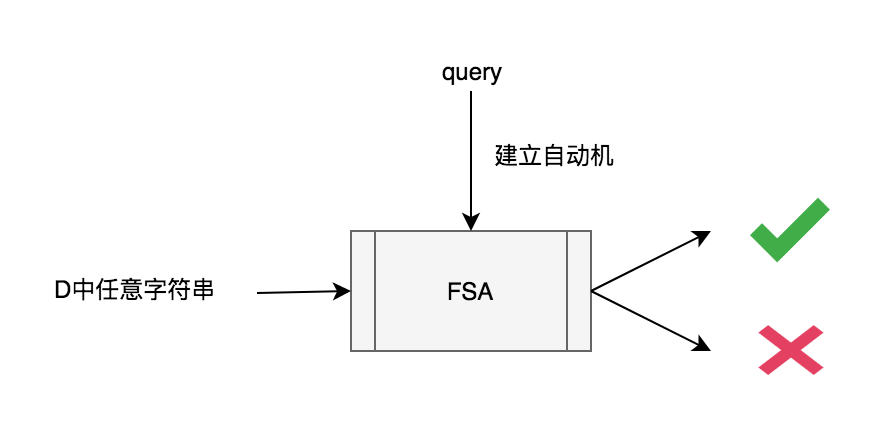
利用Levenshtein Automata，对比之前的动态规划，我们把 O(MN) 算法提升到了 O(N) ，对于D中大量的字符串来说，至少这是一个优化。当然这个算法并不是只有这个优点。

等一下，什么是有限状态自动机？让我们一步一步来。

Finite State Automaton (FSA)

如果你尝试搜索有限状态自动机，复杂的数学模型和难懂的术语可能让你晕头转向。

但对于这个算法来说，我们只需要简单理解FSA即可。

可以把FSA成一个有向图，图里的节点是状态。这个有向图有一个入口，我们从入口进入，然后输入给FSA的字符串的每一个字符，就是一个指导我们沿着图中的相应的边转移到下一个状态的命令。

图中是一个很简单的例子，从左边入口进入状态1。假设输入的query字符串为FOOD，则字符F让我们转移到状态2，接下来两个字符O都会使我们沿着边回到状态2，最后D让我们到达状态3。这里的状态3有黑色的圈，表示FSA中的接受状态。如果query字符串是FOO，那么最终我们会停留在状态2，就表示FSA不接受这个字符串。

图中的示例对于每个状态，同样符号的边只有一个，这样的FSA称为确定有限状态自动机(deterministic finite automaton, DFA)。还有一种非确定有限状态自动机NFA（参考下图）。它可以由同一状态发出多条相同符号的边，而且允许空边的存在，用 \epsilon 来表示，即不需要输入也可以通过这条边转移到下一个状态。

我们简单了解了FSA，那么下一步就是如何根据query构建它呢？

构建NFA

样例及下文示例代码来自Nick Johnson's Blog

这里给出了一个样例的NFA。

这个状态机的入口是左下角，由于包含了 \epsilon 空边，所以这是个NFA。首先理解每个状态中的数字是什么意思。每个状态的形式是 n^e ，其中 n 是走到当前状态消耗的字符数， e 表示错误数，也就是编辑距离。由于我们的query是food，有四个字符，n是2，最多距离为2，所以右上角的状态是 4^2 。

再看图中的边，有三种类型的边，分别是 * ， \epsilon 以及字符。其中水平向右的边都是字符边，表示输入当前边上符号的字符时候转移，意思是不做编辑。向上的 * 边表示插入操作，这个操作不消耗输入字符（相当于一种空边）但是需要一次编辑，所以由 0^0 转移到的下一个状态是 0^1 。向右上方的边表示一次替换操作，这个既需要消耗一个输入字符，又需要一次编辑。向右上方的 \epsilon 边表示删除操作。

图中最右侧的三个状态是黑色的圈，也就是接受状态。如果输入一个字符串，最终状态停在4^0,4^1,4^2 这三个状态的话，表示这个字符串和food在距离2内相似。

如果这样还是很抽象的话，让我们举个例子。

假设输入了前两个字母f和x，我们可能会暂时停在以下几个灰色状态。

比如我们消耗第一个f向右移动，然后消耗x字符做替换操作（原始的第二个字符应该是o）向右上移动，到达状态 2^1 。如果接下来是od，那么我们可以接受fxod。事实上恰好是第二个字符o做一次替换操作得到fxod。

又比如我们消耗f向右移动，又进行删除操作向右上移动，再消耗一个x做替换操作，到达状态 3^2 。如果接下来的输入是d，那么我们可以接受fxd。事实上food恰好删除第二个字符且替换第三个字符可以得到fxd。

所以灰色的六个状态是所有可能的当前状态，随着输入更多的字符，这些状态会不断进行状态转移。最终输入所有的字符，停在某几个可能的状态。如果这些状态中存在接受状态，则可以说明我们经过某些操作可以把输入的字符串转化成food，也就是说可以接受这个输入的单词。

相信我，当你看懂这个图之后，会有一种很奇妙的感觉。

其实构造这样的NFA并不复杂，下面是python的实现。

def levenshtein_automata(term, k):
  nfa = NFA((0, 0))
  for i, c in enumerate(term):
    for e in range(k + 1):
      # Correct character
      nfa.add_transition((i, e), c, (i + 1, e))
      if e < k:
        # Deletion
        nfa.add_transition((i, e), NFA.ANY, (i, e + 1))
        # Insertion
        nfa.add_transition((i, e), NFA.EPSILON, (i + 1, e + 1))
        # Substitution
        nfa.add_transition((i, e), NFA.ANY, (i + 1, e + 1))
  for e in range(k + 1):
    if e < k:
      nfa.add_transition((len(term), e), NFA.ANY, (len(term), e + 1))
    nfa.add_final_state((len(term), e))
  return nfa

可以看出构造这样的一个NFA的复杂度是 O(kN) ，这里的k很小，通常为2或3（Lucene内的n=2）所以可以近似看成N的线性时间。

咦？好像不对啊，虽然构造起来很快，可是在NFA中进行状态转移，每一步都有多种情况，事实上计算量反而更多了呀。

于是我们需要把NFA转换成DFA。在计算理论中，NFA和DFA是等价的。但DFA中对于每一个转移，下一个活跃状态是确定的，所以计算是非常高效的。

构建DFA

这里是个由query=food建立的DFA，输入任意单词，如果最终落在粗的圆圈上，即接受状态，则表示这个单词的编辑距离与food小于等于1。

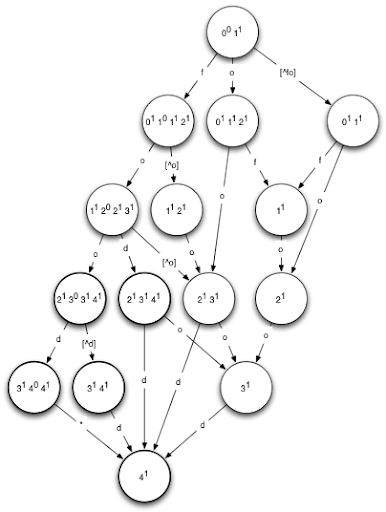
这个图要比之前NFA好理解的多，不信我们再来个例子试试。假如我们有单词feod。那么状态转移的过程应该是

0^01^1\rightarrow0^11^01^12^1\rightarrow1^12^1\rightarrow2^13^1\rightarrow4^1

最后的状态是接受状态，所以输入的单词我们认为是与food相似的。怎么样，是不是很简单？

可以发现，在DFA中的计算是非常的高效。但是如何从NFA构造一个DFA呢？

标准的方法是幂集构造（Powerset Construction）。然而这种方法的最坏时间是 O(2^n) 。指数复杂度的算法我们是不能接受的。可是并不要太担心，首先对于Levenshtein Automata来说是不会接近最坏时间的，其次，我们甚至有 O(n) 的算法来构造DFA ^{[1]} ，甚至有一些跳过构造DFA的步骤而是基于表格的算法。（Lucene内的实现就非常神奇，有兴趣可以去研究一下）

更高效的搜索

到这里我们已经了解了如何高效的构造Levenshtein Automata了，当然还有一个问题就是如何更高效的搜索D中的单词。

一种方法是将D本身看做DFA。字典集D常用数据结构如Trie，是一种特殊的DFA。将D和Levenshtein Automata进行交运算。也就是同时遍历两个DFA，并且只沿着相同的边前进。当两个DFA都到达了接受状态，则当前的单词可以作为结果集中的一个输出。

def intersect(dfa1, dfa2):
  stack = [("", dfa1.start_state, dfa2.start_state)]
  while stack:
    s, state1, state2 = stack.pop()
    for edge in set(dfa1.edges(state1)).intersect(dfa2.edges(state2)):
      state1 = dfa1.next(state1, edge)
      state2 = dfa2.next(state2, edge)
      if state1 and state2:
        s = s + edge
        stack.append((s, state1, state2))
        if dfa1.is_final(state1) and dfa2.is_final(state2):
          yield s

这种方法适用于以DFA的形式进行存储的字典集。

然而还有很多字典是以某种sorted list的形式存储在内存里，又或者以BTree的方式在硬盘中，这该怎么办呢？

Naive的方法是从最小的字符串依次放到自动机中遍历，然而我们可以做一些改进。由于Levenshtein Automata像一个有向图。如果某个错误的字符串最后落在了某个拒绝状态，可以从这个状态开始回溯搜索，找到自动机里按字典序的停在下一个接受状态的单词。我们只需要把自动机做一点预处理，让搜索的时候从每一个状态的最小字典序的边开始，就可以简单快速的找到下一个可接受的单词。这就意味着在有序的字典D中可以直接跳过这个单词之前的所有错误情况，极大提高了遍历的效率。

到这里，这篇文章就结束啦！如果你认真地读到了这里，相信你应该弄懂了基本的原理。

接下来会继续分享更多有趣的内容的。

默默匿去读书啦。ε=ε=ε=ε=ε=┌(;￣◇￣)┘

参考

[1] Fast string correction with Levenshtein automata

[2] http://blog.notdot.net/2010/07/Damn-Cool-Algorithms-Levenshtein-Automata