ML4. 对数几率回归与广义线性模型

为什么线性模型是可行的？

几何意义——生成子空间

假设有 N 个实例 \mathbf{x_i} = (x_0, x_1, x_2, \cdots, x_n) ，x_i(i \neq 0) 代表了实例的第 i 个属性， x_0 = 1 。

那么下列矩阵就变成了 N×(n 1) 维的数据矩阵 \mathbf{X}，它的每一行表示同一个样本的不同属性，每一列表示不同样本中的相同属性。 \begin{aligned} \left [ \begin{aligned} --\mathbf{x_1^\top} -- \\ --\mathbf{x_2^\top} --\\ --\dots -- \\ --\mathbf{x_N^\top}-- \\ \end{aligned} \right ] \end{aligned} \\\\ 模型是 h(\mathbf{x})=\mathbf{w}^\top \mathbf{x}=\sum_{i=0}^{n} w_{i} \cdot x_{i} ，最优解为 \mathbf{w^*} = (\mathbf{X^\top} \mathbf{X} )^{-1} \mathbf{X^\top} \mathbf{y} = X^\dagger \mathbf{y} ，代入 E_\mathrm{in}(\mathbf{w}) = \frac{1}{N} \| \mathbf{X}\mathbf{w} - \mathbf{y} \| ^2，得： \begin{aligned} E_\mathrm{in}(\mathbf{w^*}) & = \frac{1}{N} \| \mathbf{X}\mathbf{X}^\dagger \mathbf{y} - \mathbf{y} \| ^2 \\ & = \frac{1}{N} \| \mathbf{y} - \mathbf{X}\mathbf{X}^\dagger \mathbf{y} \| ^2 \\ & = \frac{1}{N} \| (\mathbf{I} - \mathbf{X}\mathbf{X}^\dagger) \mathbf{y} \| ^2 \\ & = \frac{1}{N} \| (\mathbf{I} - \mathbf{H} ) \mathbf{y} \| ^2 \end{aligned} \\\\ 注：投影矩阵 P ∈ \mathbb{R}_{n×n} 是正交投影矩阵的充要条件 P^\top = P

如果待拟合数据任意两个属性都线性无关的话，\mathbf{X} 就可以看成一个由它的所有列向量所张成的空间。

属性的数目 n 会远远小于数据的数目 N，因此 \mathbf{X} 张成的是 N 维空间之内的 n 维生成子空间，或者叫 n 维超平面。这个超平面的每一个维度都对应着数据集的一个列向量。理想条件下，输出 \mathbf{y} 作为属性的线性组合，也应该出现在由数据属性构成的超平面上。但受噪声的影响，真正的 \mathbf{y} 是超平面之外的一个点，这时就要退而求其次，在超平面上找到离 \mathbf{y} 最近的点作为最佳的近似。

• 黄色区域表示由所有属性张成的超平面；
• 黑色向量 \mathbf{x_1} 和天蓝色向量 \mathbf{x_2} 表示输入向量；
• 红色实线 \mathbf{y} 表示真实输出，水平的红色虚线 \mathbf{\hat{y}} 表示数据的最优估计值（属性的线性组合）；
• 垂直的红色虚线表示 \mathbf{y} - \mathbf{\hat{y}} （残差），它与超平面正交。

如果我们假设 \mathbf{w^*} 是上帝所知道的规律，那 \mathbf{Xw^*} 也仍然在 \mathbf{X} 的张成空间里。但是由于噪声 \mathbf{z} 的影响使得 \mathbf{y} 出现了偏差。 \mathbf{Xw^*} \mathbf{z} = \mathbf{y} \\\\

这就使得 \begin{aligned} E_\mathrm{in}(\mathbf{w^*}) &= \frac{1}{N}\sum_{i=1}^{N}(\mathbf{y} - \mathbf{\hat{y}})^2 \\ &= \frac{1}{N}\sum_{i=1}^{N}((\mathbf{I} - \mathbf{H})\mathbf{y})^2 \\ &= \frac{1}{n}\sum_{i=1}^{N}((\mathbf{I} - \mathbf{H})\mathbf{z})^2 \\ \end{aligned} \\\\ 还可以看成，这里把 \mathbf{x} 变成了它的转置（虽然输出的结果没有不同）。\mathbf{w}^\top \mathbf{x} 背后的寓意是每个包含若干输入属性和一个输出结果的样本都被视为一个整体，误差分散在不同的样本点上；而当输出被写成 \mathbf{x}^\top \mathbf{w} 时，每个单独属性在所有样本点上的取值被视为一个整体，误差分散在每个不同的属性上。

注意我们之前令 \mathbf{x} = (x_0, x_1, x_2, \cdots, x_n) ，x_i(i \neq 0) 代表了实例的第 i 个属性， x_0 = 1 ： h(\mathbf{x})=1 \cdot w_{0} \sum_{j=1}^{n} x_{j} \cdot w_{j}=\mathbf{x}^{\top} \mathbf{w} \\\\

概率视角——最大似然估计 MLE

高斯噪声是最复杂的噪声，我们一般认为噪声服从正态分布： \epsilon \sim N(\mu, \sigma^2) \\\\ 真实的f() 受到噪声的影响才有了 {y}： y = f(\mathbf{x}) \epsilon = \mathbf{w^\top}\mathbf{x} \epsilon \\\\

y 在条件下满足概率分布： y|_{\mathbf{x_i};\mathbf{w}} \sim N(\mathbf{\mu} \mathbf{w^\top}\mathbf{x}, \sigma^2) \\\\

其概率密度函数为： f_y(y) = \frac{1}{\sqrt{2\pi} \sigma}exp({-\frac{[y - (\mathbf{\mu} \mathbf{w^\top}\mathbf{x})]^2} {2 \sigma^2}}) \\\\ 根据最大似然估计得出似然函数： L(\mathbf{w}) = \prod_{i=1}^{N}f_y(y) \\ \begin{aligned} ln(L(\mathbf{w})) &= \sum_{i=1}^{N} \frac{1}{\sqrt{2\pi} \sigma}exp({-\frac{[y - (\mathbf{\mu} \mathbf{w^\top}\mathbf{\tilde{x}})]^2} {2 \sigma^2}}) \\ &= \sum_{i=1}^{N} ln(\frac{1}{\sqrt{2\pi} \sigma}) - {\sum_{i=1}^{N} \frac{[y - (\mathbf{\mu} \mathbf{w^\top}\mathbf{\tilde{x}})]^2} {2 \sigma^2}} \\ &= \sum_{i=1}^{N} ln(\frac{1}{\sqrt{2\pi} \sigma}) - {\sum_{i=1}^{N} \frac{[y - (\mathbf{\mu} \mathbf{w^\top}\mathbf{\tilde{x}})]^2} {2 \sigma^2}}\\ &= \sum_{i=1}^{N} ln(\frac{1}{\sqrt{2\pi} \sigma}) - {\sum_{i=1}^{N} \frac{[y - ( \mathbf{w^{*\top}}\mathbf{x})]^2} {2 \sigma^2}} \end{aligned} \\\\ 最大化似然函数： \begin{aligned} \mathbf{w^*} &= \arg \max _{\mathbf{w^*}}L(\mathbf{w}) \\ &= \arg \max _{\mathbf{w^*}}\sum_{i=1}^{N} ln(\frac{1}{\sqrt{2\pi} \sigma}) - {\sum_{i=1}^{N} \frac{[y - ( \mathbf{w^{*\top}}\mathbf{{x}})]^2} {2 \sigma^2}} \\ &= \arg \min _{\mathbf{w^*}} {\sum_{i=1}^{N} \frac{[y - ( \mathbf{w^{*\top}}\mathbf{x})]^2} {2 \sigma^2}} \\ &= \arg \min _{\mathbf{w^*}} {\sum_{i=1}^{N} [y - ( \mathbf{w^{*\top}}\mathbf{x})]^2 } \end{aligned} \\\\

对数几率回归

回归就是通过输入的属性值得到一个预测值，是否可以通过一个联系函数，将预测值转化为离散值从而进行分类呢？线性几率回归正是研究这样的问题。

为了解决一个最简单的二类分类问题, 我们为每一个点定义一个值域 [0, 1] 的函数, 表示这个点分在A类或者B类中的可能性, 如果非常可能是A类, 那可能性就逼近 1 , 如果非常可能是B类, 那可能性就逼近0（相对A的可能性）。

我们引入一个对数几率函数（logistic function ，logit 函数，也叫 sigmoid 函数）来实现实数集到 [0, 1] 的映射。将预测值投影到0-1之间，从而将线性回归问题转化为二分类问题。 y = \frac{1}{1 e^z} \\\\

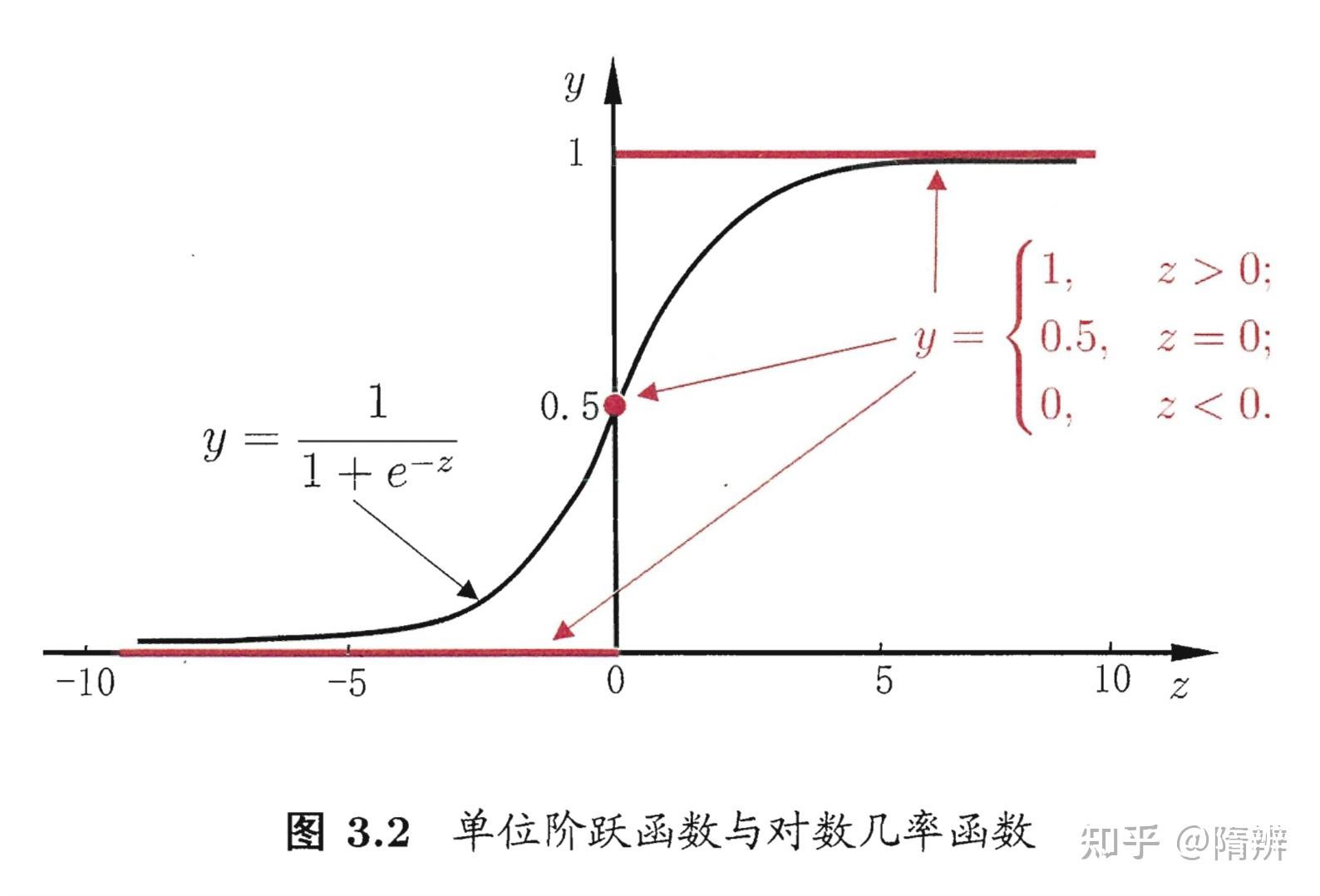
一个事件发生的几率(odds)是指该事件发生的概率与该事件不发生的概率的比值。如果事件发生的概率是 p，那么该事件的几率为\frac{p}{1-p} ，该事件的对数几率是：

logit(y) = \ln \frac{y}{1-y} \\\\ 由我们输出的得到： \ln \frac{p(y=1 \mid \mathbf{x})}{p(y=0 \mid \mathbf{x})}=\mathbf{w}^{\mathrm{T}} \mathbf{x} b \\\\

\begin{array}{l} p(y=1 \mid \mathbf{x})=\frac{e^{\mathbf{w}^{\mathrm{T}} \mathbf{x} b}}{1 e^{\mathbf{w}^{\mathrm{T}} \mathbf{x} b}} \\ p(y=0 \mid \mathbf{x})=\frac{1}{1 e^{\mathbf{w}^{\mathrm{T}} \mathbf{x} b}} \end{array} \\\\

同样用 MLE： \ell(\mathbf{w})=\sum_{i=1}^{m} \ln p\left(y_{i} \mid \mathbf{x}_{i} ; \mathbf{w}\right) \\\\

会得到所谓的误差函数，也叫做交叉熵： E_\mathrm{in} = \ln(1 \exp(-y\mathbf{w^\top x})) \\\\

我们的批量损失函数一般是这样的： \mathrm{Lost}\left(h_{\theta}(x), y\right)=\left\{\begin{array}{ll} -\log \left(h_{\theta}(x)\right) & y=1 \\ -\log \left(1-h_{\theta}(x)\right) & y=0 \end{array}\right. \\\\ 合并为这个式子： \mathrm{Lost}\left(h_{\theta}(x), y\right)=-y \log \left(h_{\theta}(x)\right)-(1-y) \log \left(1-h_{\theta}(x)\right) \\\\

广义线性模型

考虑所有 y 的衍生物的情形，就得到了“广义的线性模型”（generalized linear model），其中，g 称为联系函数（link function）。 y=g^{-1}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x} b\right) \\\\ 之前的对数几率回归就是代入了 g(c) = \ln \frac{c}{1-c}