强化学习3：价值函数和Bellman方程

学而不思则罔

几乎所有的强化学习问题都涉及到对价值函数 v(s)（评估当前状态）或是 q(s,a) （评估当前所给状态下某个行为）的评估，根据强化学习的目标，它们评估的内容就是当前Agent所能够获得的回报值的期望。

1、价值函数

Agent在运行过程中总会遵循一定的行为模式，比如走迷宫时总喜欢向左走，这就是一种行为模式，这种行为上的选择我们称之为策略，表示为 \pi ，而价值函数也与之息息相关。当Agent一直以策略 \pi 运行时，那么它在状态s可期望的回报就是：
v_{\pi}(s)=E[G_{t}|S_{t}=s]=E[\sum_{k=0}^{\infty}{\gamma ^{k}R_{t+k+1}|S_{t}=s}]

或者是在状态s下执行行为a的期望回报是：
q_{\pi}(s,a) = E[G_{t}|S_{t}=s,A_{t}=a]=E[\sum_{k=0}^{\infty}{\gamma ^{k}R_{t+k+1}|S_{t}=s,A_{t}=a}]

其实根据回报值的公式展开，我们可以接着得到一个迭代公式：
v_{\pi}(s) = E_{\pi}[G_{t}|S_{t}=s]

=E_{\pi}[R_{t+1}|+\gamma G_{t-1}|S_{t=s}]

=\sum_{a}^{}{\pi(s|a))}\sum_{s'}^{}{\sum_{r}^{}{p(s',r|s,)[r+\gamma E_{\pi}[G_{t+1}|S_{t+1=s'}]]}}

=\sum_{a}^{}{\pi(a|s)\sum_{s',r}^{}{p(s',r|s,a)[r+\gamma v_{\pi}(s')]}}

这个迭代式其实就是Bellman方程的基本表现形式，它表明了当前状态s下Agent所能够获得的期望回报值与其后继状态之间存在关联。如下图所示，空心圆代表状态，实心圆代表行为，在状态s是Agent面临三个选择，而促使Agent在三个行为中进行选择的就是策略 \pi ，它代表着一个概率分布，即从所有行为中选择不同行为的概率。在选择了行为a之后，Agent同样会有不同的可能性转换到不同的新状态，这个概率就是转换概率p，而新状态就是s'，在转换的过程中Agent也会获得环境的相应回报，即是r。

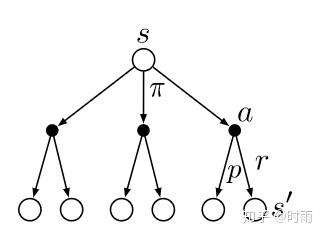
Bellman方程在强化学习中应用非常广泛。它的存在告诉了我们：

值函数可以通过迭代计算得到！

2、最优策略和最优值函数

因为在强化学习中我假定的是有限的马尔可夫决策过程，因此其状态集，行为集都是有限的，所以Agent所有的行为策略也是有限的。那么在这至少存在一个最优策略，强于或等效于其他所有的策略，我们定义其为 \pi* 。那么如何评价一个策略的好坏呢？其实很简单，强化学习的最终目标就是尽可能地多获得回报值，那么很自然的，当 v_{\pi'}\geq v_{\pi} 时就有 \pi'\geq\pi ，而对于最优策略，其值函数的值也必然是最大的： v_{*}(s)=\max_{\pi}v_{\pi}(s) ，同样的，对于最优动作价值函数我们可以得到： q_{*}(s,a)=\max_{\pi}q_{\pi}(s,a) 。

当我们对公式进行迭代展开之后就可以得到：

v_{*}(s) = \max_{a\in A}q_{_{\pi_{*}}}(s,a)

=\max_{a}E_{\pi_{*}}[G_{t}|S_{t}=s,A_{t}=a]

=\max_{a}E_{\pi_{*}}[R_{t+1}+\gamma G_{t+1}|S_{t}=s,A_{t}=a]

=\max_{a}\sum_{s',r}^{}{p(s',r|s,a)}[r+\gamma v_{*}(s')]

以及对于动作价值函数：

q_{*}(s,a)=E[R_{t+1}+\gamma \max_{a'}q_{*}(S_{t+1},a')|S_{t}=s,A_{t}=a]

=\sum_{s',r}^{}{p(s',r|s,a)[r+\gamma \max_{a'}q_{*}(s',a)]}

这个式子我们称之为Bellman最优化方程。在式中价值函数的迭代不依赖于策略，迭代方向是当前状态下的最优value值，而动作价值函数的迭代方向则是当前策略下的最优值，下图就是其示意图：