1.1 二元运算、等价关系和分划、同余关系

前言

道可道，非常道。名可名，非常名。——老子

抽象代数是一门语言，是解放思想的神兵，是认识世界本质的利器。

此抽象代数笔记是对邓少强老师的教学视频的总结。预备知识有集合基础知识、映射的概念、线性代数基础。线性代数不是必需的，只是介绍例子会用到。

目录

1.1 二元运算、等价关系、同余关系

导论

这一节主要讲一些基本概念以及明确抽象代数的研究对象——代数系统（集合+运算）。S0介绍了映射有关的基础概念，熟悉的可以跳过。S1介绍几个有用的概念，只需要知道名词的意义即可，交换图也要有个大概的映像，以后会经常用到。S2要掌握什么是二元运算，谈及二元运算就就要知道默认运算是封闭的。S3讲了关系和等价关系，这个要好好理解。要知道关系本质上是集合。等价关系本质上是做分类。今后在证明等价关系时，基本都是验证等价关系的三个性质。而在思考等价关系的意义时，基本都是从集合的分类去考虑。S4介绍了同余关系，同余关系的等价关系特殊的一种，它能够使商集继承原集合的运算。要计算两个商集的运算结果，只需对代表元进行运算，所得结果再取商集即可

Section 0 映射、单射、满射

定义0.1 （映射、像、原象）

设 A,B 是两个集合， f 称为 A 到B的映射，如果对任意的 a\in A , B 都存在 \color{red}{唯一} 的元素 f(a)\in B 与之（指代 a ）对应. 符号记做 f:A\to B 。此时 f(a) 称作 a 的像，而 a 称作 f(a) 的原像。另外，用符号「 \mapsto 」强调元素的对应，故映射 f 「把 a\in A 映射到 f(a) \in B 」记做： a \mapsto f(a) .

特别地，恒等映射 i: A\to A ,定义为 i(x)=x, \forall x\in A

定义 0.2 （单射、满射、双射）

设A,B 是两个集合，有映射 f:A\to B 。

(i) 称 f 是单射(injective)，如果 A 中任意两个不同的元素在 f 下的像都不同。用数学语言表述即是： \forall a,b \in A, a\not =b \Rightarrow f(a)\not=f(b) ,逻辑等价于 \forall a,b \in A, f(a)=f(b) \Rightarrow a =b

(ii) 称 f 是满射(surjective)，如果对 B 中任一元素在 A 中都存在原象。 用数学语言表述即是： \forall b\in B\Rightarrow\exists a\in A,f(a)=b .

(iii) 称 f 是双射（或一一映射）如果 f 即是单射又是满射

注1： \Delta 证明单射常用“ \forall a,b \in A, f(a)=f(b) \Rightarrow a =b ”这个技巧
注2： \Delta 证明满射，常用定义 \forall b\in B\Rightarrow\exists a\in A,f(a)=b 这个技巧，即是：先任意取 B 中一元素 b ,然后通过推理，找到 A 中一元素 a , 使得 a 和 b 满足关系 f(a)=b
注3： \Delta 证明双射，就是要证明即是单射，又是满射

定义 0.3 (复合映射）

设A,B,C 是集合，有映射 f:A\to B 和 g:B\to C . 定义 f 和 g 的复合映射 g\circ f :A \to C 为： (g\circ f)(x)=g(f(x)), \forall x\in A

定义0.3 （左逆、右逆、逆）

设A,B 是集合，有映射 f:A\to B 和 g:B\to A .

(i) 称 g 是 f 的左逆（映射），如果 g\circ f=i （ i 是恒等映射）

(ii) 称g 是 f 的右逆（映射），如果 f\circ g=i

(iii) 如果 g 即是 f 的左逆，又是f 的右逆，就称 g 是的逆（映射）。此时将 g 记做 f^{-1} .

命题0.1 （理解单射、满射、左逆、右逆的好题目）

设A,B 是两个集合，有映射 f:A\to B，证明：

(1) f 有左逆当且仅当 f 是单射；

(2) f 有右逆当且仅当 f 是满射；

(3) f 有逆当且仅当 f 是双射；

这个题目如果能稍微想一下就理解，说明对以上映射、逆等概念是完全理解的。

定义0.4 （原象集和像集）

设A,B 是两个集合，有映射 f:A\to B 。

设有子集 A_0 \subseteq A , A_0 在 f 下的像集记做 f(A_0) ,定义为 f(A_0):=\{f(x)\in B:x \in A_0\}

设有子集 B_0\subseteq B , B_0在 f 下的原像集记做 f^{-1}(B_0) ,定义为 f^{-1}(B_0):=\{x\in A:f(x)\in B_0\}

注1：这里 f^{-1} 不代表 f 有逆，只是一个记号。上面的定义对 f 有没有逆都适用。

Section 1 有用的概念

这几个概念将会一直用到。

定义 1.1 (子集到母集嵌入映射)

设有集合 A , A_0 是 A 的子集. 定义 A_0 到 A 的嵌入映射 i:A_0\to A 为： \forall x \in A_0,\ i(x)=x .

意思就是说，将 A 中子集 A_0 的元素映射到元素本身。

定义 1.2 （映射的延拓与限制）

设有集合 A_0,A,B 且 A_0\subseteq A . 有映射 f:A\to B, \ g:A_0\to B 。如果 \forall x\in A_0 有 f(x)=g(x) ,那么就称 f 是 g 在(A上)的延拓，或称 g 是 f 在( A_0 上)的限制，记做 g=f|_{A_0} .

意思就是说, f 和 g 在子集 A_0 上的取值相等。

定义1.3 交换图

我们可以将映射画成图。在图中，复合连接不同路径上的映射若相等，则称此图可交换。

交换图是一个工具，可用于直观展示映射之间的复合，见下面例子。

例子 1.1（嵌入映射、延拓与限制的交换图）

设有集合 A_0,A,B 且 A_0\subseteq A . 嵌入映射 i:A_0\to A。映射 f:A\to B, \ g:A_0\to B ， g=f|_{A_0} 。将映射 i,f,g 画成交换图。

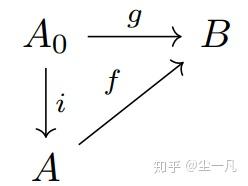
阅读交换图的方法：选定终点和起点，沿着某个路径从起点走到终点。顺着箭头，表示复合上箭头上的映射；逆着箭头，表示复合上箭头上的「逆映射」（如果逆映射存在）。
(a) 比如，选取起点 A_0 和终点 B . 从图中可以看出有两个路径，一个路径是走 g 这个箭头，一个路径是先走 i ,再走 f . 因此，从 A_0 到 B ,有 g=f\circ i （ \circ 表示映射的复合）
(b) 再比如，选取起点 A 和终点 B . 从图中可以看出有两个路径，一个路径是逆着 i ,再走 g ,一个路径是顺着 f . 因此，从 A 到 B ,有 g\circ i^{-1}=f.

定义 1.4 （集合的笛卡尔积）

设 A,B 是集合， A 和 B 的笛卡尔积（又叫直积）是一个集合，符号记做 A\times B ,定义为： A\times B=\{(a,b):a\in A,b \in B\} . 注意 (a,b) 是有顺序的。

Section 2 运算

所谓的代数体系=非空集合+运算(也叫代数系统），没有运算的集合是没有意义的。但是什么是运算？咱们先看观察一些运算。实数上的加法运算 + ，我们知道有 a+b=c ，加法运算就像一台机器，吃进去了两个实数 a,b ,生出来一个实数 c . 再来看看实向量空间 V 的数乘运算,取 \lambda \in \mathbb{R} ， a \in V ，通过数乘运算，得到一个向量 \lambda a \in V . 也就是说，运算本质上是一种映射，它将某两个集合 A,B 的元素，映射成第三个集合 C 里的元素。数学定义如下：

定义2.1 （运算）

设 A,B,C 为三个非空集合，映射 f:A\times B\to C 就称为 A 与 B 到 C 的运算。

给定 a\in A,b\in B ,则运算结果 f(a,b)\in C

注：因为笛卡尔积 A\times B 是有顺序的，因此,不一定有 f(a,b)=f(b,a)

如果上面定义中的 A,B,C 是同一个集合，那么这种运算就叫二元运算。

定义 2.2 （二元运算）

设 A 为非空集合，映射 f:A\times A\to A 称为 A 上的二元运算。给定 a,b\in A ,则运算结果 f(a,b)\in A。

今后二元运算如果很明确的，不会混淆的情况下，就简称运算。

注1："给定 a,b\in A ,则运算结果 f(a,b)\in A", 这个描述就是所谓的“封闭性”，即是说，对集合 A 元素运算的结果仍属于 A 。今后提到二元运算，就要想到这个运算对所定义的集合是封闭。
注2：对群的定义里，有些书明确写着封闭性，有写书没有明确写封闭性。原因就在于，有些书已经定义了二元运算，因此默认是封闭的。有些书只是提了运算，因此明确要求封闭。

参与运算的元素个数很多，用 f(a,b) 的方式来表示运算就很麻烦，比如 f(f(c,f(a,b)),d) 是不是看晕了。好在很早以前我们就发现了可以用「连接符」来表示运算了，比如我们将 f 命名为连接符 \diamond ,即用 a\diamond b 表示 f(a,b) . 那么 f(f(c,f(a,b)),d)=(c\diamond(a\diamond b))\diamond d （注意加括号表示先运算）,是不是一目了然呢！

这样一来，运算的结果看起来就会很简单，也有助于发现运算规律，今后若 A 在定义了某个二元运算（比如命名为 \odot），就记做有序对 (A,\odot) ,其中第一个位置表示集合，第二个位置表示运算 \odot ；如果不强调运算符，那么就干脆不写运算符

我们知道，对于实数的加法运算有结合律、交换律；对于实数的加法和乘法运算，他们配合下有分配律。也就是说，运算有三个基本规律，即结合律、交换律和分配律，严格定义如下

定义 2.3 （交换律、结合律、分配律）

设非空集合 A 上定义了二元运算 \otimes

(i) 交换律：如果 \forall a,b \in A ,有 a\otimes b=b\otimes a ,就称运算 \otimes 满足交换律。

(ii) 结合律：如果 \forall a,b \in A ,有 a\otimes (b \otimes c)=(a\otimes b)\otimes c ,就称运算 \otimes 满足结合律。

设非空集合 A 上定义了两个运算 \otimes和 \oplus ，设 a,b,c\in A

(iii) 如果满足 a\otimes (b\oplus c)=(a\otimes b )\oplus (a\otimes c) ,就称 \otimes 对 \oplus 有左分配律

(iV) 如果满足 (b\oplus c)\otimes a=(b\otimes a )\oplus (c\otimes a) ,就称 \otimes 对 \oplus 有右分配律

注1：交换律是描述两个元素的运算能够交换位置; 结合律是描述"先算后算"的问题
注2：并不是所有的运算都存在以上三种规律。
注3：如果满足结合律，则 a\otimes (b \otimes c) 和 (a\otimes b)\otimes c 的结果是一致的，因此以后不再区分，都记做 a\otimes b\otimes c

\Delta 如果 (A,\circ) 满足结合律，则可定义元素的「幂」，即 a^n=\underbrace{a\circ a\cdots\circ a}_{n 个a}, \quad n \in \mathbb{N}'

如果 (A,\circ)还满足交换律，则有 (a\circ b )^n=a^n \circ b^n

\begin{align} (a\circ b )^n&=\underbrace{(a\circ b )\circ (a\circ b )\cdots\circ (a\circ b )}_{n 个(a\circ b )}\\ &=a\circ b \circ a\circ b \cdots\circ a\circ b \quad(结合律)\\ &=\underbrace{(a\circ a\cdots \circ a)\circ(b\circ b\cdots \circ b)}_{交换位置,把a换到前面,把b换到后面}\quad(交换律)\\ &=a^n \circ b^n \end{align}

当集合是元素是有限时，集合上的运算可以用运算表来表示。比如设A 有四个元素， A=\{a,b,c,d\} ,定义了运算 \circ 如下表所示。

思考：如果运算满足交换律，那么这个表有什么特征？（答案：关于对角线对称的元素相等）

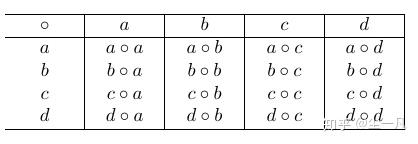
例子 2.1

设集合 A=\{a,b,c,d\} ,在 A 上定义了运算 \oslash 如下表所示，请验证 (A,\oslash) 是否满足结合律？是否满足交换律？

注：这个例子我是让 \{e, e^2, e^3, e^4\} 是循环群，令a=e,b=e^2,c=e^3,d=e^4 构造出来的。

(i) 验证结合律：
(a) (a\oslash a)\oslash a=b \oslash a=c ; a\oslash (a\oslash a)=a \oslash b=c ;因此 (a\oslash a)\oslash a=a\oslash (a\oslash a) ;
同理 (b\oslash b)\oslash b=b\oslash (b\oslash b)=b ; (c\oslash c)\oslash c=c\oslash (c\oslash c)=a ;
(d\oslash d)\oslash d=d\oslash (d\oslash d)=d
(b) (a\oslash b)\oslash c=c \oslash c=b ; a\oslash (b\oslash c)=a \oslash a=b ;因此 (a\oslash b)\oslash c=a\oslash (b\oslash c) ;
同理 (a\oslash b)\oslash d=a\oslash (b\oslash d)=c ; (a\oslash c)\oslash d=a\oslash (c\oslash d)=d
(b\oslash c)\oslash d=b\oslash (c\oslash d)=a
综上， 是否满足结合律。
(ii) 交换律可以直接从表中看出，因为表中关于对角线的对称的元素相等。

Section 3 关系与等价关系

“关系”一词在生活也是经常用到，比如“父子关系”“朋友关系”，但到底什么是关系？首先谈论关系时，必然要涉及两个对象; 其次这两个对象在此关系下必需是明确的，要么有这个关系，要么没有这个关系。不允许出现没法判断有没有关系的情况。举个例子，"父子关系”必需涉及两个人，其次任意两个人都可以判断有没有“父子关系”，不会出现没法判断这两个是不是父子关系的情况。

将上面叙述的，改写成集合语言。设有集合 A=\{世界上所有的人\} ，关系 R=父子关系 。那么对 A 中的所有人(元素)组对 (a,b) 都可以判断 a 和 b 有没有"父子关系".假设我们判断出来了,列出来 (a,b),(c,d),(e,f)\cdots ，也就是说有序对 (a,b),(c,d),(e,f)\cdots都满足“父子关系”，我们把这些有序对放在一起组成一个集合 ，这个集合就叫做有"父子关系"的集合，记做R=\{(a,b),(c,d),(e,f)\cdots\}\subseteq A\times A ,它正是 A\times A 的子集。

将上面过程抽象出来，定义“关系”如下

定义 3.1 (关系）

设有非空集合 A , R 是 A\times A 的一个子集。对 A 中的元素 a,b ,如果 (a,b)\in R ，则称 a 和 b 有关系(relationship ) R , 记做 a Rb 。此时称 R 为 A 中的一个(二元)关系。

注：这里混用了子集 R 和关系 R 的符号，是因为本质上它们两者是同一事物。

也就是说， A 中的关系 R ,本质上是 A\times A 的子集，即 R=\{(a,b):aR b\}\subseteq A\times A 或者 aRb \Leftrightarrow(a,b)\in R

注1： aRb \Leftrightarrow(a,b)\in R 读作「 a 和 b 有关系 R ,等价于有序对 (a,b) 属于子集 R 」
注2：构造一个关系可以这样做：从 A\times A 中，画出一个子集 R .如果有序对 (a,b) 落在这个子集里面，就定义为 a 和 b 有这种关系；如果有序对 (a,b) 落在这个子集外面，就定义为 a 和 b 没有这种关系。
注3：今后定义等价关系时，一般这么写： xRy\Leftrightarrow x,y满足(你所规定的)性质
另外，关系是一种客观的事物（本质上是集合），事物可以命名，比如命名为 R 、命名为 \sim 都可以。（名可名非常名——老子）

例子3.1

(a) 设集合 A=\{a,b,c,d\} ,在 A 上定义了运算 \oslash 如下表所示。我们定义关系 R 为 ：对任意 x,y \in A ，xR y\Leftrightarrow x\oslash y=a , 试找出关系 R 代表的集合，并判断 a 和 c 是否有关系 R ?

(i)由定义的关系 xR y\Leftrightarrow x\oslash y=a 知， x 和 y 有关系，就是说 x 和 y 进行 \oslash 运算要等于 a 。从表中可以直接找出运算结果等于 a 的有序对为: (a,d),(b,c),(c,b),(d,a) .因此关系 R=\{(a,d),(b,c),(c,b),(d,a)\} ,它确实是 A\times A 的子集。
(ii) a 和 c 没有关系 R。判断方法有两种:(a) a\oslash c=d\not =a ,故 a,c 没有关系；或(b) 因为有序对 (a,c)\notin R=\{(a,d),(b,c),(c,b),(d,a)\} ,故 a,c 没有关系。

有些关系很特殊，叫做“等价关系”,两个元素等价，就可以看成是同一个事物。初中学过的全等三角形，就是一种“等价关系”。对于全等三角形，有这样的性质：(a)自己和自己全等；(b) A和B全等，则B也和A全等；(c) A和B全等，B和C全等，则推出 A和C全等。这三个性质分别叫做「反身性」,「对称性」和「传递性」。也就是说，等价关系是一种特殊的关系，特殊在于，它必须满足这三个性质。定义如下

定义3.2 （等价关系）

设 R 是非空集合 A 的一个关系，如果对任意 a,b,c\in A 满足：

(i) 反身性(reflexivity) : 对任意 a\in A , a R a ;

(ii) 对称性(symmetry): 若有 a Rb ,则有 b R a

(iii) 传递性(transitivity)：若有 a Rb,bRc ,则有 a R c

注：今后要验证一个关系是不是等价关系，就要验证这三个条件。

例子3.2 (被m除具有相同余数是一种等价关系)

记 \mathbb{Z}=\{\cdots,-1,0,1,\cdots\} 为所有整数构成的集合，令 m=5 。任取 x,y \in \mathbb{Z} ，定义关系 R : \color{red}{x Ry\Leftrightarrow x,y除以m有相同的余数} 。那么，请问

(i) 请问13和4有没有关系 R ? 6和11有没有关系 R ?-12和-3有没有关系 R ?

(ii) 请问如上定义的关系 R 是不是等价关系？

注：我们规定余数只能是正整数，负整数也可以做整除求余数。比如 -4\div 5=(-1)\times 5+1 ,故-4除以5的余数是1

由关系 R 的定义可知, x 和 y 有关系 R ,必需 x,y 除以 m=5 的余数要相同。
(i)直接求余数验证。
(a) 13\div5=2\times5+3 ,因此13除以m=5得到的余数是3；而4除以m的余数是4。两个余数不相等，因此13和4没有关系 R .
(b)6除以m的余数是1,而11除以m的余数也是1.因此6和11有关系 R .
(c) -12\div5=(-3)\times5+3 ,故 -12除以m的余数是3；而 -3\div5=(-1)\times5+2 ,故-3除以m的余数是2. 两个余数不相等，故-12和-3没有关系。
(ii)利用等价关系的三个条件验证。设 a,b,c \in \mathbb{Z}
(a)验证反身性。对任意的a, a和a除以m有相同的余数，因此 aRa .
(b)验证对称性。若 a Rb ,说明a,b除以m有相同的余数,也即是b,a 除以m有相同的余数，也即是 bRa . 因此 a Rb 可以推出 bRa .
(c) 验证传递性。若有 a Rb,bRc . 即是a,b除以m有相同的余数，b,c除以m有相同的余数. 自然 a,c除以m也有相同的余数，也即是 a Rc . 因此 a Rb,bR c\Rightarrow a Rc

例子3.2中，其实 m 的取法可以是任意正整数。"被m除具有相同余数"这种关系就简称为「模 m 的同余关系」。我们发现 \color{red}{x,y除以m有相同的余数} 等价于 \color{red}{x-y能被m整除} ，记做 m|(x-y) 。下面两个问题务必理解。

例子3.3 (很重要的例子）

设 x,y,a,b \in \mathbb{Z} , m 是正整数。

(1)证明： \color{red}{x,y除以m有相同的余数} \Leftrightarrow m|(x-y) ;

(2) 定义关系 \equiv\ (\text{mod}\ m) : a\equiv b\ (\text{mod}\ m)\Leftrightarrow m|(a-b) ,这个关系称为「模m的同余关系」，证明：模m的同余关系是等价关系。

(1) 先证 \Rightarrow 方向。
若x,y除以m有相同的余数，则可设 x=k_1m+r, y=k_2m+r ,其中 0\leq r<m 。那么 (x-y)=(k_1-k_2)m ,即是 (x-y) 能被m整除，也即m|(x-y)。
再证 \Leftarrow 方向。
设 m|(x-y) ，则有 x-y=km ,然后如何说明 x,y 有相同的余数呢？想到这里我好像做不下去了，然后我继续观察已经推得的条件 x-y=km 想，如果 x,y 没有相同的余数呢？那么就有x=k_1m+r_1, y=k_2m+r_2其中 r_1\not=r_2 。把 x,y 带入式子 x-y=km ，得到 (k_1-k_2)m+(r_1-r_2)=km ,那么左边不能被 m 整除，右边可以被 m 整除，这就产生了矛盾。因此x,y 只能有相同的余数。
综合上面两个方向就完成了证明。


(2)证明等价关系，依然要验证等价关系3个条件。
(a)验证反身性。因为 m|(a-a)=m|0 ,因此 a\equiv a\ (\text{mod}\ m)
(b)验证对称性。设 a\equiv b\ (\text{mod}\ m) ,即有 m|(a-b) ，也即 a-b=km ,也即 b-a=(-k)m ,也即 m|(b-a) ,也即 b\equiv a\ (\text{mod}\ m)
(c)验证传递性。设 a\equiv b\ (\text{mod}\ m),b\equiv c\ (\text{mod}\ m) ,即有 m|(a-b),m|(b-c) ,也即 (a-b)=k_1m,\ \ (b-c)=k_2m 因此 a-c=(a-b)+(b-c)=(k_1+k_2)m ,也即 m|(a-c) ,也即 a\equiv c\ (\text{mod}\ m) 。

对于「模m的同余关系」这个「等价关系」，我们发现，它将整数集 \mathbb{Z} 按照余数作了分类。比如取 m=5 ,那么一个整数除以 5 得到的余数只有5种情况，分别是0,1,2,3,4。也就是说模 5 ，将整数集 \mathbb{Z}分成了 5 类，分别是 \bar{0},\bar{1},\bar{2},\bar{3},\bar{4} ,分别定义为：

\bar{0}=\{模5余数是0\}， \bar{1}=\{模5余数是1\} ， \bar{2}=\{模5余数是2\} ， \bar{3}=\{模5余数是3\} ， \bar{4}=\{模5余数是4\} 。

比如，整数 -5,0,5,10\in \bar{0} ;整数 -4,1,11 \in \bar{1} 。这5个集合是整数集\mathbb{Z}的子集，且是不相交的，而且5个集合的并集就是\mathbb{Z}，即是 \mathbb{Z}=\bar{0}\cup\bar{1}\cup\bar{2}\cup\bar{3}\cup\bar{4}

也就是说，通过「模m的同余关系」这个「等价关系」，可以将定义的集合分成不相交的集类，对于任意元素，总可以知道它属于哪一类。 对于其他的等价关系，也有这个性质：一个等价关系决定了集合的分类，反之给定集合的一个分类，就决定了一个等价关系；等价关系和集合的分类本质上是一回事。 接下来就来介绍这些内容。

定义3.3 （集合的分划/分类）

集合 A 的划分(partition of set)是 A 的非空子集构成的集合，使得 A 中每个元素 x 都属于且只属于其中一个子集（指代 A 的子集）.

集合的分划，也叫集合的分类。

注1：定义有点绕，我们剖析一下。首先, A 的分划是一个集合, 记做 P_A ; 其次，这个集合的元素是 A 的子集 A_i 。于是 P_A=\{A_i\} 。拥有这两个条件还不够，因为对任意 x\in A , x 只能属于其中一个 A_i ,这同时要求 A_i\cap A_j=\varnothing 且 \cup A_i=A 。
综上，我们将分划的定义用数学语言表达如下： 集合的一个分划 P_A是下面集合的元素 \{\{A_i\}: A=\cup A_i\ \text{ and }\ A_i\cap A_j=\varnothing ,i\not=j\}
注2： \{\{A_i\}: A=\cup A_i\ \text{ and }\ A_i\cap A_j=\varnothing ,i\not=j\} 经常用。

例子3.4

设集合 A=\{a,b,c,d,e\} ,试判断下面哪些是集合 A 的分划

(1) \{\{a\},\{a,b\},\{b,c,d,e\}\}

(2) \{\{a,b\},\{c,d\},\{e\}\}

(3) \{\{a,c\},\{b,d\}\}

(4) \{\{a,b,c,d,e\}\}

(1) \{\{a\},\{a,b\},\{b,c,d,e\}\} 不是 A 的划分。因为其中 \{a\}\cap\{a,b\}=\{a\} 。
(2)\{\{a,b\},\{c,d\},\{e\}\}是 A 的分类。意思是说， A 中元素 a,b 属于一类， c,d 属于同一类， e 单独成一类。
(3) \{\{a,c\},\{b,d\}\} 不是 A 的分类，虽然里面的子集都是不相交的，但是并集不能拼成 A ，即 A\not =\{a,c\}\cup\{b,d\}
(4) \{\{a,b,c,d,e\}\} 是A的分类。 意思是说， A 中所有的元素都属于同一类。

在现实生活中，属于同一类的事物应该是相同的（等价的），这就启发我们构造这样的一个等价关系：如果两个元素属于同一类，就定义它们等价。之前我们说过"一个等价关系决定了集合的分类；给定集合的一个分类，就决定了一个等价关系"。按照这种等价关系，下面就来证明后半句话。

定理3.1-1

集合 A 中的一个分划(分类）决定 A 中的一个等价关系。

设 \{A_i\} 是 A 的一个分划，即 A=\cup A_i 且 A_i\cap A_j=\varnothing,i\not=j 。
定义关系 \sim ： a\sim b\Leftrightarrow 存在A_i,使得a,b \in A_i 。


下面证明关系 \sim 是等价关系，只需验证反身性、对称性、传递性。
(a) 验证反身性：
根据分划的定义，任意元素 a 都属于某个 A_i ,即 a\in A_i .因此 a\sim a
(b) 验证对称性：
设 a\sim b ,即是存在子集 A_i ，使得a,b \in A_i ，自然也是 b,a \in A_i ,因此 b\sim a
(c) 验证传递性：
设 a\sim b, b\sim c ,即是存在 A_i ,使得 a,b \in A_i ;存在 A_j ,使得 b,c \in A_j 。 现在问题是 A_i 和 A_j 相不相等，当然是相等的。若 A_i\not= A_j , 因为同时 b\in A_i,b\in A_j ,即是 A_i\cap A_j\not=\varnothing ,而这与我们一开始分划 \{A_i\} 的构造相矛盾（我们构造要求 A_i\cap A_j=\varnothing,i\not=j ）。因此A_i 和 A_j 是相同的。因此有 a,c\in A_i(=A_j) ,即是 a\sim c 。

证明断言"一个等价关系决定了集合的分类；给定集合的一个分类，就决定了一个等价关系"前半句话的过程，产生了很多新概念。下面引进新概念，证明自然水到渠成。

定义3.4 （等价类和代表元）

设集合 A 上定义了等价关系 \sim 。 那么对任意 a\in A , 定义 a (所在)的等价类为 A 中所有与 a 等价的元素组成的集合，记做 \bar{a} ，即\bar{a}:=\{x\in A:a\sim x \} 。

任何属于 \bar{a} 的元素就称为代表元，比如 a 就是 \bar{a} 的代表元。（或者说，与 a 等价的元素都是代表元）

注1： a 的等价类的符号常用 \bar{a},\ [a] 等等，看具体如何说明。
注2：稍微来理解一下这个定义。首先 a 的等价类 \bar{a} 是一个集合，由定义 \{x\in A:a\sim x \} 它由 A 中所有和 a 等价的元素构成。根据反身性有 a\sim a ,故 a\in \bar{a} ,即 \bar{a} 不是空集，是有意义的。

例子 3.5

设 \mathbb{Z} 是整数集，令 m=5 , 在 \mathbb{Z} 上有「模m的同余关系」,由例子3.3 我们已经知道，这是一个等价关系。问题：

(1) 求出 2 的等价类 \bar{2} ;

(2) 7是不是 \bar{2}的代表元？

「m的同余关系」是指 ：
(a) "同余"二字是指相同的余数，即被5除有相同的余数。有时从这一点想很方便。
(b)或用数学描述， a\equiv b\ (\text{mod } m)\Leftrightarrow m|(a-b)

(1) 这里 m=5 。 设与 2 等价的元素是 x ,即是 x\equiv2 \ (\text{mod} \ 5)\Leftrightarrow 5|(x-2) .这意味着 x-2=5k ,即是 x=5k+2 ,其中 k \in \mathbb{Z} .
因此 2 的等价类 \bar{2}=\{5k+2: k\in \mathbb{Z}\} .
(2) 要判断 7 是不是 \bar{2} 的代表元，有多种方法。
(a) 验证 7 \in \bar{2} ,因为 7=5\times1+2 ,故符合 \bar{2} 中元素的形式。 故 7 是代表元。
(b) 验证 7 和 2 是否等价，验证的方法有两种：
（b'）按照 a\equiv b\ (\text{mod } m)\Leftrightarrow m|(a-b) 验证。 因为 5|(7-2) ,因此 7\equiv2\ (\text{mod } 5) ,故 7 是代表元。
（b''）按照同余的意义"被5除有相同的余数"验证。7除以5的余数是2; 2除以5的余数也是2. 因此7,2除以5 有相同的余数，因此 7 等价于 2 （ 7\equiv2\ (\text{mod } 5) ）,故 7 是代表元.

定义3.5 （商集）

设集合 A 上定义了等价关系 \sim，在此等价关系下， A 中所有元素(所在)的等价类组成的集合称做 A 对 \sim 的商集（quotient set）,记做 A/ \sim . 即是： A/\sim\ :=\{\bar{a}:a\in A\} .

注1：商集 A/ \sim 是一个集合，里面的元素是等价类 \bar{a} (提醒一下，等价类是 A的子集，即是\bar{a}\subseteq A )

例子3.6

设 \mathbb{Z} 是整数集，令 m=5 , 在\mathbb{Z} 上有「模m的同余关系」,我们知道，这个关系是等价关系，我们命名为 R . 请求出 商集\mathbb{Z}/R 。

我们已经知道，\mathbb{Z} 模 5 可以得到 5 种等价类，分别是 \bar{0},\bar{1},\bar{2},\bar{3},\bar{4}。
因此商集 \mathbb{Z}/R=\{\bar{0},\bar{1},\bar{2},\bar{3},\bar{4}\} , 商集 \mathbb{Z}/R 有5个元素。
由集合分划（分类）的定义可知，商集 \mathbb{Z}/R 是 \mathbb Z 的一个分划(分类）

例子3.6里可以看出，我们在集合上定义了一个等价关系，得到一个商集，这个商集就是原集合的一个分划，也即是“一个等价关系决定一种集合的分类”，证明如下：

定理3.1-2

集合 A 中的一个等价关系决定 A 中的一个分划(分类）

设在 A 中定义了等价关系 R , 可作出商集 A/R ,下面证明商集 A/R是 A 的一个分划.
A/R=\{\bar{a}:a\in A\} ,我们先明确要证明的是什么。我们要证明的是，商集里的元素 \bar{a} 能够拼成集合 A ,且商集里的元素(子集)是互不相交的。写成数学语言就是，证明： A=\bigcup_{a\in A}\bar{a} 且如果\bar{a}\cap\bar{b}=\varnothing .
（i）先证明 A=\bigcup_{a\in A}\bar{a} 。这是一个集合相等的等式，证明的技巧就是证明两个集合互相包含，而证明集合包含的技巧就是利用包含的定义“如果 x\in A\Rightarrow x\in B ，则有 A\subseteq B ”.
（a）设 x\in A ,则 x\in \bar{x} ( x 属于自身的等价类）,而A/R 的定义是所有等价类组成的集合，故 \bar{x}\in A/R . 因此 \bar{x}\subseteq \bigcup_{a\in A}\bar{a} (原因: \bigcup_{a\in A}\bar{a} 是所有等价类的并集，而 \bar{x} 是其中一个等价类)， 因此 x \in \bigcup_{a\in A}\bar{a} . 即 A\subseteq\bigcup_{a\in A}\bar{a} 。
（b）设 x \in \bigcup_{a\in A}\bar{a} . 由并集的定义, x 属于其中某个集合，不妨设为 \bar{x} ，即使 x\in\bar{x} .而每个等价类都是 A 的子集，即是 \bar{x}\subseteq A . 两者结合就有 x\in A 。即 A\supseteq\bigcup_{a\in A}\bar{a}
综合(a)和(b)就有 A=\bigcup_{a\in A}\bar{a} 。
（ii）接着取出商集 A/R 两个元素，设 \bar{a}\not=\bar{b} ,证明 \bar{a}\cap\bar{b}=\varnothing 。
反证法，设 \bar{a} 交 \bar{b} 不等于空集，则存在元素 x 同时属于 \bar{a} 和 \bar{b} 。而 x 属于\bar{a}，说明 x 和a等价; x 属于\bar{b}，说明 x 和b等价。 那么由等价关系的传递性，就有 a 和 b 等价。而a 和 b 等价，说明 a 和 b 在同一个等价类里，即是 \bar{a}=\bar{b}。这就和\bar{a}\not=\bar{b}产生了矛盾。因此不同的等价类是不相交的。

综合定理3.1-1和定理3.1-2,就得到我们要证明的结论：

定理3.1 （集合上的等价关系和分划等价）

集合 A 中的一个等价关系 \Leftrightarrow A 中的一个分划(分类）

例子3.7

设集合 A=\{a,b,c,d,e,f\} .

(1) 我们定义集合 A 的分类为: \{\{a,b\},\{c,d,f\},\{e\}\} ,即是 A=\{a,b\}\cup\{c,d,f\}\cup\{e\} .请写出这个分类代表的等价关系。

(2)假设(1)中你已经写成等价关系 R ,思考如何写出 A 的分类。

(1)提示：比如 \{c,d,f\} 表示 c,d,f 等价。那么c和c要等价，c和d等价，d和c等价，c和f等价，f和c等价，d和d等价，d和f等价，f和d等价，f和f等价。
(2) 提示：可以将A\times A 里的点用坐标表示出来，一目了然。

例子3.8

设 R 是非空集合 A 的一个关系，并且有对称性和传递性。有人断定R是一个等价关系，推理如下:

“对 a,b\in A ，由 aRb 得到 bRa （对称性)，又从传递性得 aRa ，因而有自反性，因此 R 是一个等价关系”。请问推理对吗？

不对。只需从「等价关系本质上是集合的分类」理解。
举个例子设 A=\{a,b,c,d,e\} .
（思考过程：我们规定a,b,c属于一类，d属于一类，e不属于任何一类。那么我们就得到 \{a,b,c\},\{d\} 两个子集。因为缺了元素 e ,故两个子集不能并成 A . 但这样规定的确实是一个关系，且满足对称性和传递性。把这个思考过程写成数学语言如下）
构造关系 \begin{align} R=&\{(a,a),(b,b),(c,c),(a,b),(b,a),\\ &(a,c),(c,a),(b,c),(c,b),(d,d)\} \end{align} 可以验证这个关系具有传递性和对称性，但对于元素 e\in A 不存在反身性，因此 R 不是 A 上等价关系。

在 A 在定义等价关系 R 之后，我们得到了商集 A/R . 那么 A 到 A/R 有一个很“自然”的映射，就是把 A 中的任一元素 x 对应到它所在的等价类 \bar{x} . 这个自然映射定义如下。

定义3.6 （自然映射）

设集合 A 中定义了等价关系 \sim ，则称映射 \pi:A\to A/ \sim,\quad\pi(a)=\bar{a} 是A 到 A/\sim 的自然映射。

接下来介绍一个定理，这个定理讲了这样的道理：对于多对一的映射（满射），可以把映到同一目标的元素看成是同一类——philosophy

定理3.2

设 f:A \to B 是一个满射，在 A 中定义关系 R: a Rb\Leftrightarrow f(a)=f(b) ,则 R 是 A 的一个等价关系。又设 \pi:A\to A/R 为自然映射，则有 A/ R 到 B 上的双射 \bar{f} ,满足 \bar{f}\pi=f 。即是下图是交换图。

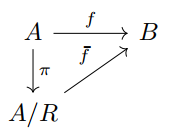
这个定理证明分两个部分，第一部分是证明 R 是一个等价关系；第二部分是构造出双射 \bar{f}


注1: 先读懂这个关系 R: a Rb\Leftrightarrow f(a)=f(b) 。 这个关系是说，如果元素 a,b\in A 映到 B 中同一元素，则定义 a,b 是有关系的。验证反身性、对称性、传递性即可证明这是一个等价关系。以验证传递性为例，设 a Rb ,bRc ,即是说 a和b映到同一B中元素 y ，b和c映到同一元素 y' ,因为b不可能映射两个不同的元素（映射的定义），故 y=y' ,因此a和c映到同一元素y=y'。因此 a Rc .即证明了传递性。

注2：如和构造出映射 \bar{f}:A/R\to B . A/R 中的元素是等价类 \bar{a} ，\bar{a}由 A 中所有和 a 映到同一元素 f(a)\in B 的元素构成。因此只需将 \bar{a} 映到 f(a) 能实现一一对应（双射）。故定义映射 \bar{f} (\bar{a})=f(a) 即可。

注3：这个定理以后有不同的版本
这个定理就不严格证明了，进一步理解见下面例子。

例子3.9

设集合 A=\{a,b,c,d,e\}, B=\{1,2,3\} . 因为 A 的元素个数比 B 的元素个数多，故从 A 到 B 的映射只能是满射。比如我们可以定义映射 f:A\to B 为： f(a)=1,f(b)=1 , f(c)=2,,f(d)=2 , f(e)=3 . 问题：

(1)定理3.2说的的等价关系 R 是什么？商集 A/R 是什么？

(2)请你构造出映射 \bar{f} 满足定理3.2的要求 \bar{f}\pi=f 。

(1) 等价关系 R 说的就是，映到同一元素的等价。 因此a,b等价；c,d等价；e等价。
写成集合分类就是： R=\{\{a,b\},\{c,d\},\{e\}\} .因此 A=\{a,b\}\cup\{c,d\}\cup\{e\}
商集A/R=\{\{a,b\},\{c,d\},\{e\}\}
我们命名 \bar{a}:=\{a,b\},\ \bar{d}:=\{c,d\},\ \bar{e}:=\{e\} （名字可以随便起的,但你要知道它代表的事物。这又体现了“名可名非常名”的思想）
则商集可写成 A/R=\{\bar{a},\bar{d},\bar{e}\}
(2) 构造映射 \bar{f}: A/R \to B 如下： \bar{f}(\bar{a})=f(a)=1 , \bar{f}(\bar{d})=f(c)=2 , \bar{f}(\bar{e})=f(e)=3 .(注意这三个式子的第二个等号中的 a,c,e 都是代表元，你也可以选择其他同一类的代表元)。这样构造出来的\bar{f}: A/R \to B是一一对应。
我们来验证是否有 \bar{f}\pi=f 。
以元素 c 为例。左边 \bar{f}\pi(c) : c\mathop \mapsto \limits^{\pi} \{c,d\}(已命名为\bar{d})\mathop \mapsto \limits^{\bar{f}}\bar{f}(\bar{d})=2 ;
右边 f(c)=2 . 同理可验证其他元素也是成立的。因此 \bar{f}\pi=f

Section 4 同余关系

S4是本节最后一个要点，我们先来说明为什么要引入「同余关系」的概念。

在S3我们已经知道，给定一定义了等价关系 R 的非空集合 A ，可以得到商集合 A/R .

如果 A 中定义了运算 \ast ，那么自然就会问商集A/R是否也存在运算？若存在，这个运算能够由原来集合 A 的运算\ast诱导出。 商集A/R肯定可以定义运算了，但我们希望运算是从运算\ast诱出来的，如下面这样子：

设 A/R 的运算是 \overline{\ast}，则对 \bar{x},\bar{y} \in A/R 希望有：\bar{x} \ \bar{\ast}\ \bar{y}=\overline{x \ast y} 。这个运算就是说，两个等价类去运算，等于先对代表元进行运算，再取等价类。 这样的定义是用代表元去算的，问题是代表元是可以随便取的，那么怎么保证取不同的代表元的运算结果是一致的呢？即是：

我们从 \bar{x} 取两个不同的代表元 x_1,x_2 (即 x_1 Rx_2,x_1\not =x_2 )。 从我们从 \bar{y} 取两个不同的代表元 y_1,y_2 (即是 y_1R\ y_2, y_1\not =y_2). 那么根据等价类运算的定义，就有：

\bar{x} \ \bar{\ast}\ \bar{y}=\overline{x_1 \ast y_1} 和 \bar{x} \ \bar{\ast}\ \bar{y}=\overline{x_2 \ast y_2} .

为了 \bar{x} \ \bar{\ast}\ \bar{y} 的运算结果相同，就必需有 \overline{x_1\ast y_1}=\overline{x_2 \ast y_2} .

而这个式子正是说明 x_1 \ast y_1 和 x_2 \ast y_2 是属于同个等价类，也就是 (x_1 \ast y_1 )\ R \ (x_2 \ast y_2) 。

因此，我们从 x_1 Rx_2 和 y_1 Ry_2 ,可以得出 (x_1 \ast y_1 )\ R \ (x_2 \ast y_2) ，也就是说我们找到了保证商集运算一致的必要条件，同时这个条件也是充分的（留作练习）。

也就是说，不是所有的等价关系 R 都可以使得商集继承原集合的运算，只有等价关系 R 满足条件：x_1 Rx_2 , y_1 Ry_2 \Rightarrow (x_1 \ast y_1 )\ R \ (x_2 \ast y_2),才可以使得商集继承原运算，满足条件的等价关系就叫做关于「运算 * 的同余关系」。定义如下：

定义4.1 （同余关系）

设非空集合 A 定义了二元运算 \star ，如果 A 的等价关系 R 满足：对任意 x_1,x_2,y_1,y_2\in A ,有 x_1Ry_1,x_2Ry_2\Rightarrow(x_1\star x_2 )R(y_1\star y_2) ,则称 R 为 A 中关于运算 \star 的同余关系。 此时元素 a\in A 所在的等价类 \bar{a} ,也叫做 a 的同余类。

注1：同余关系是等价关系的一种
注2： \Delta 只要是同余关系，等价类的运算就可以用代表元去算（画重点！）
注3：同余关系的命名来源于数论的「模m的同余关系」，见下面例子

例子4.1

设 \mathbb{Z} 是整数集，令 m=5 , 在 \mathbb{Z} 上的「模m的同余关系」是等价关系 R ，即 a\equiv b\ (\text{mod} \ m )\Leftrightarrow m|(a-b) 。我们已知道商集 \mathbb Z/R=\{\bar{0},\bar{1},\bar{2},\bar{3},\bar{4}\} 。问题：

(1)验证模m的同余关系在“加法 + ”和“乘法 \times ”下都是如定义4.1的同余关系

(2)将 \overline{14} 化成最简形式（即 \bar{a}, 0\leq a<m ）。请问 \bar{2}\times \bar{7} 是否等于 \bar{4}\times\bar{6} ?

(1) (a)验证模m的同余关系是关于加法运算“+”的同余关系。
设 x_1\equiv y_1(\text{mod } m),x_2\equiv y_2(\text{mod } m) 要验证 x_1+x_2\equiv y_1+y_2(\text{mod } m)
因为 x_1\equiv y_1(\text{mod } m) ，故 m|x_1-y_1 .同理 m|x_2-y_2 。根据整除的性质， m|((x_1-y_1)+(x_2-y_2)) ,即是 m|((x_1+x_2)-(y_1+y_2)) ,也即 x_1+x_2\equiv y_1+y_2(\text{mod } m) 。
(b)验证模m的同余关系是关于乘法运算“ \times ”的同余关系。
设 x_1\equiv y_1(\text{mod } m),x_2\equiv y_2(\text{mod } m) 要验证 x_1\times x_2\equiv y_1\times y_2(\text{mod } m)
设 x_1\equiv y_1(\text{mod } m) ，即是 x_1-y_1=k_1m .同理 x_2-y_2=k_2m 。
接下来要证明 x_1x_2-y_1y_2 可被 m 整除。根据整除的性质，我们知道 x_1-y_1 和 x_2-y_2 的线性组合也是可以被m 整除的。因此可以设 x_1x_2-y_1y_2=r(x_1-y_1)+s(x_2-y_2) ,解出系数 r,s 即得 x_1x_2-y_1y_2=x_2(x_1-y_1)+y_1(x_2-y_2)=x_2k_1m+y_1k_2m 因此 m|(x_1x_2-y_1y_2)


(2) \overline{14} 是 14 所在的等价类，而 14 模 5 的余数是 4 ,因此 14\equiv 4 \ (\text{mod } 5) ,因此 4 和 14 等价，故也是代表元，因此 \overline{14}=\overline{4} .
由(1)知，模m的同余关系在乘法下是同余关系，因此等价类的运算可以用代表元去运算。下面就用代表元去运算后再取等价类。
\bar{2}\times \bar{7}=\overline{2\times 7}=\overline{14}=\overline{4} \ (\text{mod }5) ,而 \bar{4}\times\bar{6}=\overline{4\times 6}=\overline{24}=\overline{4} \ (\text{mod }5)
因此 \bar{2}\times \bar{7}=\bar{4}\times \bar{6}