详解CTC

本文主要参考自Hannun等人在distill.pub发表的文章（https://distill.pub/2017/ctc/），感谢Hunnun等人对CTC的梳理。

简介

在语音识别中，我们的数据集是音频文件和其对应的文本，不幸的是，音频文件和文本很难再单词的单位上对齐。除了语言识别，在OCR，机器翻译中，都存在类似的Sequence to Sequence结构，同样也需要在预处理操作时进行对齐，但是这种对齐有时候是非常困难的。如果不使用对齐而直接训练模型时，由于人的语速的不同，或者字符间距离的不同，导致模型很难收敛。

CTC(Connectionist Temporal Classification)是一种避开输入与输出手动对齐的一种方式，是非常适合语音识别或者OCR这种应用的。

给定输入序列 X=[x_1,x_2,...,x_T] 以及对应的标签数据 Y=[y_1,y_2,..,y_U] ,例如语音识别中的音频文件和文本文件。我们的工作是找到 X 到 Y 的一个映射，这种对时序数据进行分类的算法叫做Temporal Classification。

对比传统的分类方法，时序分类有如下难点：

1. X 和 Y 的长度都是变化的；
2. X 和 Y 的长度是不相等的；
3. 对于一个端到端的模型，我们并不希望手动设计X 和 Y 的之间的对齐。

CTC提供了解决方案，对于一个给定的输入序列 X ，CTC给出所有可能的 Y 的输出分布。根据这个分布，我们可以输出最可能的结果或者给出某个输出的概率。

损失函数：给定输入序列 X ，我们希望最大化 Y 的后验概率 P(Y|X) , P(Y|X) 应该是可导的，这样我们能执行梯度下降算法；

测试：给定一个训练好的模型和输入序列 X ，我们希望输出概率最高的 Y :

Y^* = argmax_Yp(Y|X)\tag{1}

当然，在测试时，我们希望 Y^* 能够尽快的被搜索到。

算法详解

给定输入 X ，CTC输出每个可能输出及其条件概率。问题的关键是CTC的输出概率是如何考虑 X 和 Y 之间的对齐的，这种对齐也是构建损失函数的基础。所以，首先我们分析CTC的对齐方式，然后我们在分析CTC的损失函数的构造。

1.1 对齐

需要注意的是，CTC本身是不需要对齐的，但是我们需要知道 X 的输出路径和最终输出结果的对应关系，因为在CTC中，多个输出路径可能对应一个输出结果，举例来理解。例如在OCR的任务中，输入 X 是含有“CAT”的图片，输出 Y 是文本[C, A, T]。将 X 分割成若干个时间片，每个时间片得到一个输出，一个最简答的解决方案是合并连续重复出现的字母，如图2.

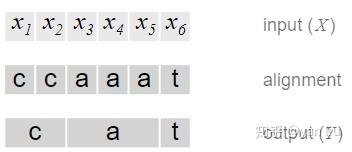
这个问题有两个缺点：

1. 几乎不可能将 X 的每个时间片都和输出Y对应上，例如OCR中字符的间隔，语音识别中的停顿;
2. 不能处理有连续重复字符出现的情况，例如单词“HELLO”，按照上面的算法，输出的是“HELO”而非“HELLO”。

为了解决上面的问题，CTC引入了空白字符 \epsilon ，例如OCR中的字符间距，语音识别中的停顿均表示为 \epsilon 。所以，CTC的对齐涉及去除重复字母和去除 \epsilon 两部分，如图3。

这种对齐方式有三个特征：

1. X 与 Y 之间的时间片映射是单调的，即如果 X 向前移动一个时间片， Y 保持不动或者也向前移动一个时间片；
2. X 与 Y 之间的映射是多对一的，即多个输出可能对应一个映射，反之则不成立，所以也有了特征3；
3. X 的长度大于等于 Y 的长度。

1.2 损失函数

CTC的时间片的输出和输出序列的映射如图4：

也就是说，对应标签 Y ，其关于输入 X 的后验概率可以表示为所有映射为 Y 的路径之和，我们的目标就是最大化 Y 关于 x = y 的后验概率 P(Y|X) 。假设每个时间片的输出是相互独立的，则路径的后验概率是每个时间片概率的累积，公式及其详细含义如图5。

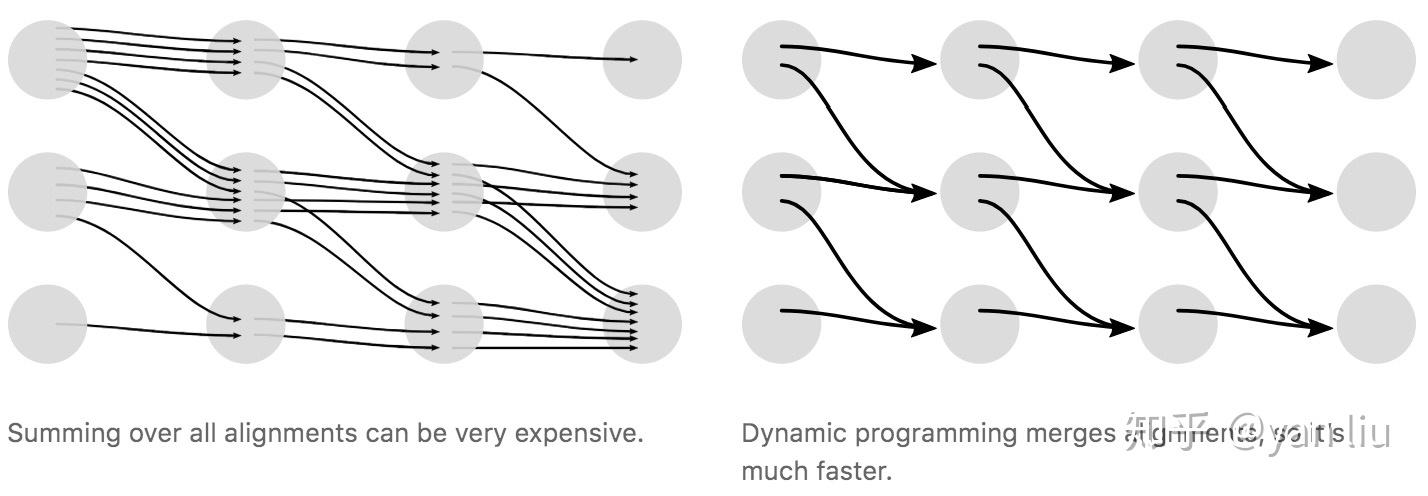
上面的CTC算法存在性能问题，对于一个时间片长度为 T 的 N 分类任务，所有可能的路径数为 N^T ，在很多情况下，这几乎是一个宇宙级别的数字，用于计算Loss几乎是不现实的。在CTC中采用了动态规划的思想来对查找路径进行剪枝，算法的核心思想是如果路径 \pi_1 和路径 \pi_2 在时间片 t 之前的输出均相等，我们就可以提前合并他们，如图6。

其中，横轴的单位是 X 的时间片，纵轴的单位是 Y 插入 \epsilon 的序列 Z 。例如对于单词“ZOO”，插入 \epsilon 后为：

Z =\{\epsilon, Z, \epsilon, O, \epsilon, O, \epsilon\}\tag{2}

我们用 \alpha_{s,t} 表示路径中已经合并的在横轴单位为 t ，纵轴单位为 s 的节点。根据CTC的对齐方式的三个特征，输入有9个时间片，标签内容是“ZOO”， P(Y|X) 的所有可能的合法路径如下图

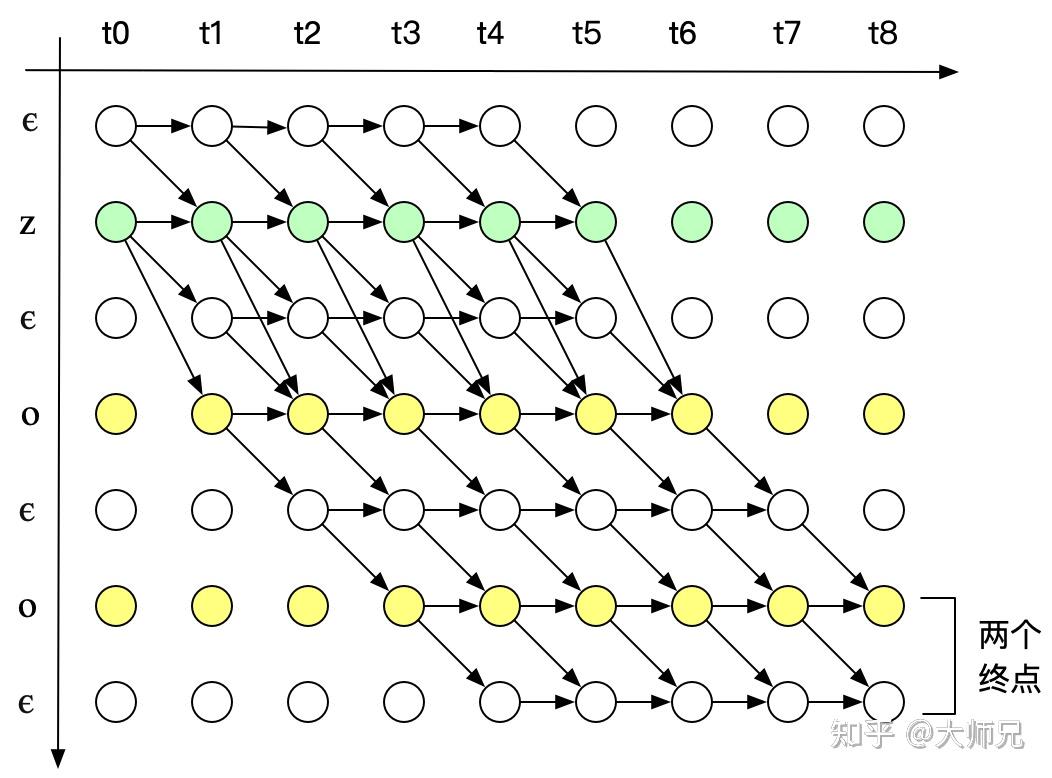
上图分成两种情况

Case 1：

如果 \alpha_{s,t} = \epsilon ， 则 \alpha_{s,t} 只能由前一个空格 \alpha_{s-1,t-1} 或者其本身 \alpha_{s,t-1} 得到，如果 \alpha_{s,t} 不等于 \epsilon ，但是 \alpha_{s,t} 为连续字符的第二个，即 \alpha_{s} = \alpha_{s-2} ，则 \alpha_{s,t} 只能由前一个空格 \alpha_{s-1,t-1} 或者其本身 \alpha_{s,t-1} 得到，而不能由前一个字符得到，因为这样做会将连续两个相同的字符合并成一个。 p_t(z_s | X) 表示在时刻t输出字符 z_s 的概率。

\alpha(s,t) = (\alpha(s,t-1) + \alpha(s-1, t-1))\cdot p_t(z_s | X) \tag{3}

Case 2:

如果 \alpha_{s,t} 不等于 \epsilon ，则 \alpha_{s,t} 可以由 \alpha_{s,t-1} ， \alpha_{s-1,t-1} 以及 \alpha_{s-2,t-1} 得来，可以表示为：

\alpha(s,t) = (\alpha(s,t-1) + \alpha(s-1, t-1) + \alpha(s-2, t-1))\cdot p_t(z_s | X)\tag{4}

从图7中我们可以看到，合法路径有两个起始点，合法路径的概率 p(Y|X) 是两个final nodes的概率之和。

现在，我们已经可以高效的计算损失函数，下一步的工作便是计算梯度用于训练模型。由于 P(Y|X) 的计算只涉及加法和乘法，因此其一定是可导函数，进而我们可以使用SGD优化模型。

对于数据集 D ，模型的优化目标是最小化负对数似然

\mathop{\sum}_{(X,Y)\in D} -logp(Y|X)\tag{5}

1.3 预测

当我们训练好一个RNN模型时，给定一个输入序列 X ，我们需要找到最可能的输出，也就是求解

Y^* = \mathop{\arg\max}_Y p(Y|X)\tag{6}

求解最可能的输出有两种方案，一种是Greedy Search，第二种是beam search

1.3.1 Greedy Search

每个时间片均取该时间片概率最高的节点作为输出：

A^* = \mathop{\arg\max}_A \prod{t=1}^T p_t(a_t | X)\tag{7}

这个方法最大的缺点是忽略了一个输出可能对应多个对齐方式.

1.3.2 Beam Search

Beam Search是寻找全局最优值和Greedy Search在查找时间和模型精度的一个折中。一个简单的beam search在每个时间片计算所有可能假设的概率，并从中选出最高的几个作为一组。然后再从这组假设的基础上产生概率最高的几个作为一组假设，依次进行，直到达到最后一个时间片，下图是beam search的宽度为3的搜索过程，红线为选中的假设。

CTC的特征

1. 条件独立：CTC的一个非常不合理的假设是其假设每个时间片都是相互独立的，这是一个非常不好的假设。在OCR或者语音识别中，各个时间片之间是含有一些语义信息的，所以如果能够在CTC中加入语言模型的话效果应该会有提升。
2. 单调对齐：CTC的另外一个约束是输入 X 与输出 Y 之间的单调对齐，在OCR和语音识别中，这种约束是成立的。但是在一些场景中例如机器翻译，这个约束便无效了。
3. 多对一映射：CTC的又一个约束是输入序列 X 的长度大于标签数据 Y 的长度，但是对于 Y 的长度大于 X 的长度的场景，CTC便失效了。

参考文献

[1] Connectionist Temporal Classification : Labelling Unsegmented Sequence Data with Recurrent Neural Networks. Graves, A., Fernandez, S., Gomez, F. and Schmidhuber, J., 2006. Proceedings of the 23rd international conference on Machine Learning, pp. 369--376. DOI: 10.1145/1143844.1143891

[2] Sequence Modeling with CTC. Hunnun, Awni, Distill, 2017