卷积神经网络——深度学习第九章

继续深度学习花书的读书笔记总结，这一章主要介绍了卷积神经网络(convolutional neural network, 简称CNN), 它通常适用于具有网格状结构的数据，例如时序数据可看做是在特定时间间隔上的一维网格，图像可以看做是像素构成的二维网格，医学成像如CT等为三维网格数据。

卷积神经网络，顾名思义，利用了数学上的卷积操作(convolution)。和前面第六章总结的基本的前馈神经网络相比，CNN只不过是将某层或某几层中的矩阵乘法运算替换为卷积运算，其他的比如说最大似然法则，反向传播算法等等都保持不变。

回顾一下矩阵乘法可以表示为C=AB，矩阵中每个元素为

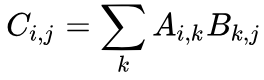
而卷积运算定义为

其中I是输入矩阵(input)，K是核矩阵(kernel)，输出S又称作特征图(feature map)，而m,n则为K的大小。卷积操作即可看做将核矩阵扫过输入矩阵并进行元素积求和的过程，如下图所示：

为什么CNN可以有这么高效的应用于具有网格结构的数据呢？主要原因是 1：稀疏连接(sparse connectivity) 2:参数共享(parameter sharing)。下面分别解释一下：

对于传统的神经网络来说，由于其操作是矩阵乘法，每一个输入与输出元之间都需要一个独立的参数来表示，这代表每个输出元与每个输入元之间都有连接，我们就需要很大的空间来存储这些参数，而对于CNN来说，通常其kernel的大小远小于其输入的大小，例如对于图像数据，输入常常有成千上万的像素，而对于检测图像中边的结构的kernel可能只需要利用十至百个像素即可，这极大的减小了存储所需空间，而且减小了计算输出时的计算量。对于m个输入和n个输出，矩阵乘法需要 个参数，其运算时间为 ，而假如我们限制每个输入到输出的连接为k个，则我们仅需要 个参数，且运算时间为 。如图中所示，上图为卷积操作，下图为矩阵乘法，可见卷积操作总的连接数大大减小

另外，对于传统神经网络来说，每一个输入至输出的元素都是独立的，只对于输入的一个元素起作用，而对于CNN来说，kernel的矩阵元素对于输入的每一个元素都起作用，实现了参数的共享，如图中所示，上图是一个kernel大小为3的卷积神经网络，其中深黑色箭头代表的kernel中间的元素对于每一个 到 的运算都起作用，而对于下图矩阵乘法来讲，黑色箭头代表的权重矩阵中的元素仅对 到 的运算起作用。

除了卷积层之外，CNN中还有常用的操作是pooling function，其作用是利用附近元素的统计信息来代替其原有的值，其目的是可以使结果在对于输入的小量改变的干扰下保持稳定。例如，一个经典的pooling function是max pooling，即将周围小方格中的最大值作为输出值，当某一输入值改变时，对最大值影响较小，保持了输出的稳定。加入pooling后，卷积的基本单元包括卷积层(convolution layer)，激活函数的非线性Detector layer，以及pooling layer，如下图所示

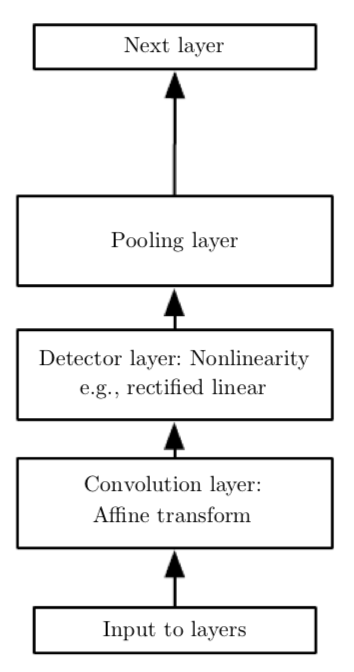
当然pooling layer实际上是假定了我们的数据对于小位移是不变的，比起特定的位置，我们更关心的是某个特征是否存在，对于有些问题，假如我们更关心其特征所在的特定位置，则我们不需用pooling layer。实际上，对于卷积操作来说，我们也是假设了隐藏层中的权重和其邻居是相同的只不过是位移了一下，而且权重集中在与该单元在空间上连续的一个小的空间内，而对于其他元素则权重为零，即我们的卷积层代表的函数是局域相互作用且平移不变的，所以我们要注意对于我们所要研究的数据convolution以及pooling是否会造成欠拟合。

CNN还有一些其他技巧如strided convolution，即我们每间隔几个元素做一次卷积，则输出相对于输入的大小进一步减小，如下图所示，图中为stride为2的卷积，输出元素个数近似为输入元素的1/2：

其他的技巧还有zero padding，即如果我们不加任何的padding，假如我们的kernel大小为k，对于一维网格的CNN，由于边缘元素的存在，则每层大小会减小k-1，这导致我们不能建立很深的CNN，所以我们可以采取对每层边缘额外补上k-1个零元素的方式，使每层大小保持一致，从而可以训练更深层的CNN。

基于基础的CNN架构，各种算法层出不穷，经典的有AlexNet，VGG，GoogleNet，ResNet等等，感兴趣的小伙伴可以参考斯坦福cs231n这节课的内容http://cs231n.stanford.edu/slides/2017/cs231n_2017_lecture9.pdf， 会详细讲解每个架构的原理， 这里仅总结基本的CNN操作及组成，万变不离其宗。CNN主要应用在图像识别领域，与下一章将要总结的RNN相结合，也可以用来进行视频识别，图像文字转换等有趣的任务。

注：截图均来自Ian Goodfellow等合著的Deep Learning一书，推荐阅读原书。