神经网络，BP算法的理解与推导

折射

intp程序员，世界的观察者

原创，转载请注明出处。

（常规字母代表标量，粗体字母代表向量，大写粗体字母代表矩阵）

这里假设你已经知道了神经网络的基本概念，并且最好看过BP算法。

可能你没有看懂，或者你跟我一样被各种公式搞晕了。尤其是学过的线性代数跟微积分知识也忘记得差不多的人，对复杂的数学公式跟符号非常不敏感的人，特别适合看这个。

希望在看完这篇文章后，能够帮助你弄懂BP算法的具体流程，以及BP算法的数学推导过程。能够对于任何给定的神经网络结构，求出对应的BP算法的训练公式。最好是能够理解到能写出代码的程度。

一、神经网络数学描述

假设给定一个神经网络，如何用数学语言来描述它？

我们来举个简单的例子，它包含一个输入层，2个隐含层，1个输出层。

（注意，本文的神经网络，是没有偏置项(bias)的，因为偏置项可以通过给每层加入一个恒为1的输入来消除掉，因此有偏置可以等价转换成没有偏置的问题。具体怎么消除类似于我之前在逻辑回归里面讲的方法）

从图中可以看出，我们的输入是一个二维的向量 \bm{x} = [x_1, x_2]^T ，输出是一个数值。

我们说的层具体指代的是图中的哪一个部分呢？

我随手画了4个方框，代表从左到右依次是：输入层，隐含层1，隐含层2，输出层。

二、输入，输出和激活函数

取隐含层1。先说这一层的输入和输出，对于这一层的每个神经元，都有一个对应的输入值，以及一个对应的输出值，它们都是一个标量，假设对于第 l 层（图里面画错了应该是l，请把图中的 n 脑补成 l ）：

我们可以将多个标量值变成一个向量值，定义：

\bm{a}_l= \left[ \begin{matrix} a^l_1 \\ a^l_2 \\ ... \\ a^l_n \end{matrix} \right] ， \bm{o}_l= \left[ \begin{matrix} o^l_1 \\ o^l_2 \\ ... \\ o^l_n \end{matrix} \right] ，

激活函数可以全部都选择sigmoid函数，但是也有每个神经元选用不一样的激活函数的情况，在这里为了更加通用，假设 f_1,f_2,f_3 用的是不同的激活函数。

在应用了激活函数以后，就能把 \bm{a}_l 转换成 \bm{o}_l ，它们的关系是：

\bm{o}_l = \left[ \begin{matrix} f_1(a^l_1) \\ f_2(a^l_2) \\ ... \\ f_3(a^l_n) \end{matrix} \right] = \bm{f}(\bm{a}_l)

因此，我们可以知道 l 层输出跟输出的关系，记作等式1：

\bm{o}_l = \bm{f}(\bm{a}_l)

三、权重

权重的值实际上就是层与层之间的连线，举个例子：

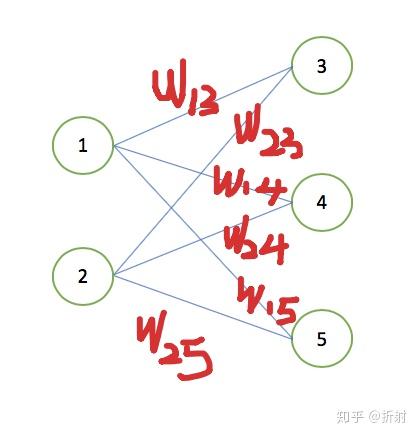
权重的作用，可以认为是对于上一层的输出向量 \bm{o}_{l-1} 做线性组合，在 l 层中，有几个神经元，就对应于对输出向量\bm{o}_{l-1}做几次线性组合。

比如 w_{13} 就代表点1连到点3的权值，我们可以把 l 层所有的权值写成一个权值矩阵 \bm{W}_l ，比如上面的图对应的权值矩阵就长这样：

\bm{W} = \left[ \begin{matrix} w_{13} & w_{23} \\ w_{14} & w_{24} \\ w_{15} & w_{25} \end{matrix} \right]

我们来看这个矩阵的含义：

上图中，\bm{W} 中的每一行代表着对右输出值的一次线性组合，对应于 l 层的一个神经元。因此矩阵有多少行，就代表着这一层有多少个神经元。

上图中， \bm{W} 的第 n 列，代表对输入的第 n 维做线性组合。因此，上一层的输出向量一共有多少个维度， \bm{W} 就对应有多少个列。

现在拿第一张图练习一下怎么把权值换成矩阵，自己动手画一画每一层对应的 \bm{W}，应该是这样子的（懒得写矩阵里面的标号了）：

我们来看这个矩阵的好处，有了这个矩阵，对\bm{o}_{l-1}做线性组合的计算就变得非常简单了。继续拿那个例子来说明，假设我们上一层的输出向量 \bm{o}_{l-1} 跟这一层的权重矩阵 \bm{W}_l ：

\bm{o}_{l-1} = \left[ \begin{matrix} o_1 \\ o_2 \end{matrix} \right] ， \bm{W}_l = \left[ \begin{matrix} w_{13} & w_{23} \\ w_{14} & w_{24} \\ w_{15} & w_{25} \end{matrix} \right]

知道了\bm{o}_{l-1} ， \bm{W}_l 以后，对\bm{o}_{l-1}做线性组合的过程，在有了矩阵这个强大的工具以后，就变得非常简单了。我们每次只需要一步操作，就能够将复杂的多次线性组合运算转变成一次矩阵左乘向量的运算，我们来感受一下这个过程：

\bm{W}_l \bm{o}_{l-1}= \left[ \begin{matrix} w_{13} & w_{23} \\ w_{14} & w_{24} \\ w_{15} & w_{25} \end{matrix} \right] \left[ \begin{matrix} o_{1} \\ o_{2} \end{matrix} \right] = \left[ \begin{matrix} w_{13}o_{1} + w_{23}o_{2} \\ w_{14}o_{1} + w_{24}o_{2} \\ w_{15}o_{1} + w_{25}o_{2} \end{matrix} \right] = \left[ \begin{matrix} a_{1} \\ a_{2}\\ a_{3} \end{matrix} \right] = \bm{a}_l

用图表示：

因此，每一层的输入对应上一层的输出对 \bm{W}_l 的线性变换，我们有这个等式：

\bm{W}_l \bm{o}_{l-1} = \bm{a}_l

四、正向传播

正向传播就是将一个样本 \bm{x}_n 输入到神经网络，从而获得输出值的过程。当训练好神经网络之后，走一遍正向传播过程就能够获得网络的输出值。

在BP算法的训练过程中，当拿到样本之后，我们做的第一步也是正向传播。

当有了矩阵这个工具以后，正向传播的过程十分简单，就是不断将输入做线性组合，再应用激活函数，转换成输出，再到下一层的输入，不断重复直到到达神经网络的最后一层。

来详细说明，首先回顾一下，前两节的最后，我们分别得到了两个非常重要的等式：

\bm{a}_l = \bm{W}_l \bm{o}_{l-1} (等式1)

\bm{o}_l = \bm{f}(\bm{a}_l) （等式2）

这两个等式非常重要，后面会一直用到，

(等式1)可以把 l 的值增加1 ，同时把 \bm{a} 变成 \bm{o} 。

(等式2)可以把 \bm{o} 变成 \bm{a}

那我们的输入的 \bm{x} 可以看做是第一层的输入 \bm{o}_0 ，用（等式1）可以转成 \bm{a}_1 ，再用（等式2）转化成 \bm{o}_1 ，我们就能够依次求出 \bm{o}_0,\bm{a}_1,\bm{o}_1,\bm{a}_2,\bm{o}_2,\bm{a}_3,\bm{o}_3,....,\bm{o}_L ，最后得到的 \bm{o}_L 就是神经网络的最终输出值。最终值所对应的数学表达式：

\bm{f}_3(\bm{W}_3\bm{f}_2{(\bm{W}_2\bm{f}_1(\bm{W}_1\bm{x_n}))}) = \bm{o}_3=y （n层的可以类推）

需要注意一点，这里的函数 \bm{f}() 我是用的粗体表示的，它不是普通的函数，而是一个向量函数。它的意思是对输入的每一个分量都应用那个节点的激活函数，它输出的也是一个向量：

\bm{f}(\bm{a}_l) = \left[ \begin{matrix} f_1(a^l_1) \\ f_2(a^l_2) \\ ... \\ f_z(a^l_n) \end{matrix} \right]

虽然实际应用中，每个点的激活函数可以都选择同一个函数。但是我们的为了公式能够通用，还是需要写成这样的形式。

具体过程直接画个图展示说明一下：

现在有个输入向量 \bm{x} 从左边进来，首先变成第1层的输入，它可以记作 \bm{o}_0 ，给它左乘一个矩阵做线性变换，直到求出最后一层的输出值：

五、BP算法

我们知道，给定一个输出，通过一次正向传播，我们就能获得输出。但是这是假设已经训练好了神经网络的情况下。然而训练网络的过程才是最难的。

下面就来介绍最经典最常用的训练网络的算法，BP算法。这个算法算是机器学习入门的一大门槛之一，估计劝退了不少人。我也是折腾了好久才搞明白这个算法的原理。下面我们来慢慢解析这个大名鼎鼎的BP算法。

BP算法是一种更新权重的方法，我们知道每一层都有一个权重 \bm{W}_l 在BP算法中，权重的更新依据是这样的：

\bm{W}_l = \bm{W}_l - \eta \frac{\partial C}{\partial \bm{W}_l}

其中 C 是我们定义的损失函数，\eta 是我们设定的学习率常数。对于回归问题，通常定义损失函数为：

C = \frac{1}{2}（o_L- y）^2

其中， L 是指代的神经网络的层数。解释一下就是求最后一层的输出与实际标签y的差值，对于只有一个输出的神经网络是这样，有的神经网络有多个输出值，需要改写成向量形式：

\bm{C} = \frac{1}{2}||\bm{o}_L- \bm{y}||^2

现在关键在于如何求出损失函数关于权值矩阵的偏导 \frac{\partial C}{\partial \bm{W}_l}

放在图里面看一下， \bm{W}_l 是中间的某一层的权重矩阵，而C是最右边的一个函数。

乍一看很懵逼，两个量之间隔了那么远，怎么能求出偏导呢？别忘了，我们之前提到过的2、3节推导出来的两个基本等式，这两个等式相当于一个桥梁，能够沟通神经网络的各个层。

\bm{a}_l = \bm{W}_l \bm{o}_{l-1} (等式1)

\bm{o}_l = \bm{f}(\bm{a}_l) （等式2）

(等式1)可以把 l 的值增加1 ，同时把 \bm{a} 变成 \bm{o} 。

(等式2)可以把 \bm{o} 变成 \bm{a}

注意到，等式1里面不是有一个 \bm{W}_l 吗？我们现在就要利用它。回头看看，我们之前得到过一个序列：

\bm{o}_0,\bm{a}_1,\bm{o}_1,\bm{a}_2,\bm{o}_2,\bm{a}_3,\bm{o}_3,....,\bm{o}_L

解释一下，这个序列的每个量之前都求出来过。并且每个量都是可以表达成它前面任何一个量的函数，所以，对于最后一项 \bm{o}_L 来说，在这个序列中选取前面的任何一项，有如下关系：

\bm{o}_L = f(任意项)

我们选取 \bm{a}_l 项，再加上等式1，可知：

\bm{o}_L = f(\bm{a}_{l})

\bm{a}_l = \bm{W}_l \bm{o}_{l-1} = g(\bm{W}_l)

由于\bm{o}_L = f(\bm{a}_{l}),\bm{a}_l = g(\bm{W}_l),所以， \bm{o}_L = f(g(\bm{W}_l)) 。

C是一个关于最后一层的输出 \bm{o}_L 的函数，假设它是 h(\bm{o}_L) ，那么它其实是一个关于 \bm{W}_l 的复合函数。根据高中学的链式求导的法则，公式可以变为：

\frac{\partial \bm{C}}{\partial \bm{W}_l} = \frac{\partial \bm{C}}{\partial \bm{a}_l} \frac{\partial \bm{a}_l} {\partial \bm{W}_l}

我们定义左边这一项为误差 \bm{\xi} ，右边可以求出来就等于 \bm{o}_{l-1} （矩阵求导公式表），定义：

\bm{\xi}_l = \frac{\partial \bm{C}}{\partial \bm{a}_l}

\bm{\xi}_l 是一个非常重要的值，它是第 l 层的误差向量。BP之所以叫做误差反向传播，就是来自于这个误差向量沿着从右往左的顺序的传播。

再来看看我们的等式：

\frac{\partial \bm{C}}{\partial \bm{W}_l} = \bm{\xi}_l \bm{o}_{l-1}^T

我们还是没有解出来它，因为我们不知道 \bm{\xi}_l 。虽然不知道它怎么求，但是我们想一个办法，类似于数学归纳法的思想，我们看看能不能找到误差向量 \bm{\xi}_l 跟上一层的误差向量 \bm{\xi}_{l+1} 的关联，就是说它的递推公式。

我们假设已经知道了 \bm{\xi}_{l+1} ，那如何才能求出 \bm{\xi}_{l} ，先从定义出发，问题可以表达为：

已知 \bm{\xi}_{l+1} = \frac{\partial \bm{C}}{\partial \bm{a}_{l+1}} ，求 \bm{\xi}_l = \frac{\partial \bm{C}}{\partial \bm{a}_l} ，

这里又要用到我们万能的等式一和等式二，还记得吗？

\bm{a}_{l+1} = \bm{W}_{l+1} \bm{o}_{l} (等式1)

\bm{o}_l = \bm{f}(\bm{a}_l) （等式2）

现在来求:

\bm{\xi}_l = \frac{\partial \bm{C}}{\partial \bm{a}_l}

等式1可以把 l 变成 l+1 ，但是需要 \bm{o}_l ，所以先用等式2结合链式法则：

\bm{\xi}_l = \frac{\partial \bm{C}}{\partial \bm{o}_l}\frac{\partial \bm{o}_l}{\partial \bm{a}_l}

对左边再用等式1做一次链式法则：

\bm{\xi}_l = \frac{\partial \bm{C}}{\partial \bm{a}_{l+1}} \frac{\partial \bm{a}_{l+1}}{\partial \bm{o}_l} \frac{\partial \bm{o}_l}{\partial \bm{a}_l}

过程：

我们再计算一下，过程中需要使用等式1跟等式2：

由图可知， \bm{\xi}_l 可以由这三个东西相乘得到：\bm{\xi}_{l+1}, \bm{W}_{l+1}^T, \bm{f'}(\bm{a}_l)

这里要小心了，这几个东西不是向量就是矩阵，不能随便直接就这么乘出来，需要注意乘的顺序，我们的先观察它的形状，确保这样乘过去是有意义的。

首先，误差是一个向量，假设 l 层有3个神经元，那就是一个三维向量， \bm{f'}(\bm{a}_l) 也是一个相同形状的向量。

\bm{\xi_i}= \left[ \begin{matrix} \xi_{i1} \\ \xi_{i2} \\ \xi_{i3} \end{matrix} \right] ，\bm{f'}(\bm{a}_l) = \left[ \begin{matrix} f'_1(a_l) \\ f'_2(a_l) \\ f'_3(a_l) \end{matrix} \right]

\bm{\xi}_{l+1}, \bm{W}_{l+1}^T 代表对 l+1 层的误差做 \bm{W}_{l+1} 变换，出来的结果也应该是一个向量，所以应该把 \bm{W}_l^T 放在左边乘，乘出来的结果再跟\bm{f'}(\bm{a}_l) 乘。

两个相同形状的向量直接点乘，相当于对于两个向量的对应位置的分量相乘，所以顺序应该是这样：

\bm{\xi}_l = (\bm{W}^T_{l+1}\bm{\xi}_{l+1}) \circ \bm{f'}(\bm{\bm{a}_l})

验证一下形状对不对，拿有2个神经元的第 l 层举例子：

形状是对的上的，说明这个乘的顺序没错了：

\bm{\xi}_l = (\bm{W}^T_{l+1}\bm{\xi}_{l+1}) \circ \bm{f'}(\bm{\bm{a}_l})

这个公式告诉我们，在确定后一层的误差向量跟权值矩阵后，我们就能求出当前层的误差向量。根据数学归纳法，我们下一步就是要找到多米诺骨牌的第一张，也就是我们的最后一层的误差，这样我们就能求出所有的误差了。

求最后一层的误差，还是从定义出发，假设最后一层是L层，则：

\begin{aligned} \bm{\xi}_L& = \frac{\partial \bm{C}}{\partial \bm{a}_L} \\ &= \frac{\partial (\frac{1}{2}||\bm{o}_L- \bm{y}||^2)}{\partial \bm{a}_L} \\ &= (\bm{o}_L - \bm{y}) \circ \bm{f'}(\bm{a}_L) \end{aligned}

（需要使用等式2，以及链式求导法则）

在这里，每个量都是已知量。因此最后一层的误差就能够求出来了，即：

\bm{\xi}_L = (\bm{o}_L - \bm{y}) \circ \bm{f'}(\bm{a}_L)

然后用误差来更新最后一层的权重 \bm{W}_L ，根据我们之前推的公式，求出 \frac{\partial \bm{C}}{\partial \bm{W}_L} :

\frac{\partial \bm{C}}{\partial \bm{W}_L} = \bm{\xi}_L \bm{o}_{L-1}^T

利用\frac{\partial \bm{C}}{\partial \bm{W}_L} 来更新最后一层的权重：

\bm{W}_L = \bm{W}_L - \eta \frac{\partial C}{\partial \bm{W}_L}

大功告成，我们现在已经可以从最后一层逐步往前更新每一层的权重，从而更新所有的权重了。

如果能坚持看到这里，相信已经差不多能够搞清楚它的数学推导过程了。放心，下面不会再有数学公式了。

六、训练过程

现在我们只解决了给一组数据如何更新权重，它叫做标准误差传播算法。它对于每个训练样本都会改变一次所有的权值。

标准误差逆传播算法 1 遍历所有训练样本 (\bm{x}_n,y_n) 1.1 进行一遍正向传播，依次求出 \bm{o}_0,\bm{a}_1,\bm{o}_1,\bm{a}_2,\bm{o}_2,\bm{a}_3,\bm{o}_3,....,\bm{o}_L 1.2 根据公式\bm{\xi}_L = (\bm{o}_L - \bm{y}) \circ \bm{f'}(\bm{a}_L) ，求出最后一层的误差 \bm{\xi}_L 1.3 根据误差 \bm{\xi}_L 和公式 \frac{\partial \bm{C}}{\partial \bm{W}_L} = \bm{\xi}_L \bm{o}_{L-1}^T， \bm{W}_l = \bm{W}_l - \eta \frac{\partial C}{\partial \bm{W}_l} ，更新权重 \bm{W}_L 1.4 从第 L-1 层直到第1层： 1.4.1 根据公式 \bm{\xi}_l = (\bm{W}^T_{l+1}\bm{\xi}_{l+1}) \circ \bm{f'}(\bm{\bm{a}_l})，算出 \bm{\xi}_l 1.4.2 根据误差 \bm{\xi}_l和公式，更新权重 \bm{W}_l

但是它的更新非常非常频繁，而且容易受到干扰。我们希望误差累积到一定程度以后再一次性更新，因此需要用累积误差逆传播算法。

我们每次更新应该是要对所有训练集的累积下来的误差再求平均，算出这个平均以后再来更新。但是这样效率太低了，每走一步的代价就是需要用到所有的训练集，而神经网络的训练集往往又非常非常的大，可以考虑用随机梯度下降。随机梯度下降法要求选择一个整体训练集的无偏估计的子集，就能够更新，关于SGD跟GD的区别可以看看我逻辑回归的那个文章：

具体做法就是：

我们把训练集随机，均匀地分成N份。我们就获得了N个整体样本的无偏估计子集。在每个子集上拿去训练，然后求出平均梯度值，更新一次权重。这样重复直到用完所有的子集。这样的速度就明显会更加快，因为每次只需要用到一小部分来进行更新。