数学随笔(9): 最速降线问题的深度探究
【摘要】文章对最速降线问题进行深入研究,探讨一些未明确的问题,发现了一些非常有趣的现象和结论。
引言
最速降线是数学史一个著名问题,一个质点由A点滑落到斜下方B点 (如下图),在不计空气阻力的情况下,沿何种曲线滑落时间最短?

学过高数的人都知道,答案是红色的摆线。即圆周上任意一点沿直线滚动形成的运动轨迹,如下图。

这里更进一步探讨的问题有:
1。摆线基园半径R如何获取?它应当与A,B点的相对位置有关。设A点为坐标原点(0,0), B点坐标为(a, b), 即两点的落差(高度)为 b, 水平距离为 a, 那么如何确立 R 与 a, b 的关系?
2。既然摆线是最速降线,对给定的坐标值 a, b,质点从A滑到B的具体时间是多少?与其他曲线相比,如图中的直线,抛物线,椭圆线,圆弧线相比,究竟能快多少?
3。在同一时刻,质点在不同曲线的位置如何确定?
带着这些问题,进入本文主题。
正文:
I:摆线基圆半径R的确立
最速降线是摆线的一部分,摆线参数方程 \begin{cases} x=R(\theta-\sin\theta)\\[2ex] y=R(1-\cos\theta)\\[2ex] \end{cases}\
当质点滑到B点时, 对应的幅角记为 \theta_{*} ,则
\begin{cases} a=R(\theta_*-\sin\theta_*)\\[2ex] b=R(1-\cos\theta*)\\[2ex] \end{cases}\
可得: R=\frac{b}{1-cos\theta_{*}}
因此先要确立 \theta_{*} 的数值。上面两式相除,得到:
\frac{a}{b}=\frac{\theta_*-sin\theta_*}{1-cos\theta_*}
记宽高比 k=\frac{a}{b} , 则有: \theta_*-sin\theta_*=k(1-cos\theta_*)
定义函数 f(\theta)=\theta-sin\theta-k(1-cos\theta)
则 \theta_* 是方程 f(\theta)=0 的根,但是该方程没有代数解。
显然 \theta_* 与宽高比 k 直接相关,从上面得知,半径 R 与 高度 b 和 \theta_* 相关。
可用牛顿求根公式获得获得 \theta_* 的数值解 :
\theta_{n+1}=\theta_n-\frac{f(\theta_n)}{f'(\theta_n)} 其中, f'(\theta)=1-cos\theta-ksin\theta
初值 \theta_0 越靠近正确的根,迭代序列收敛越快 (收敛速度为二阶的算法)。
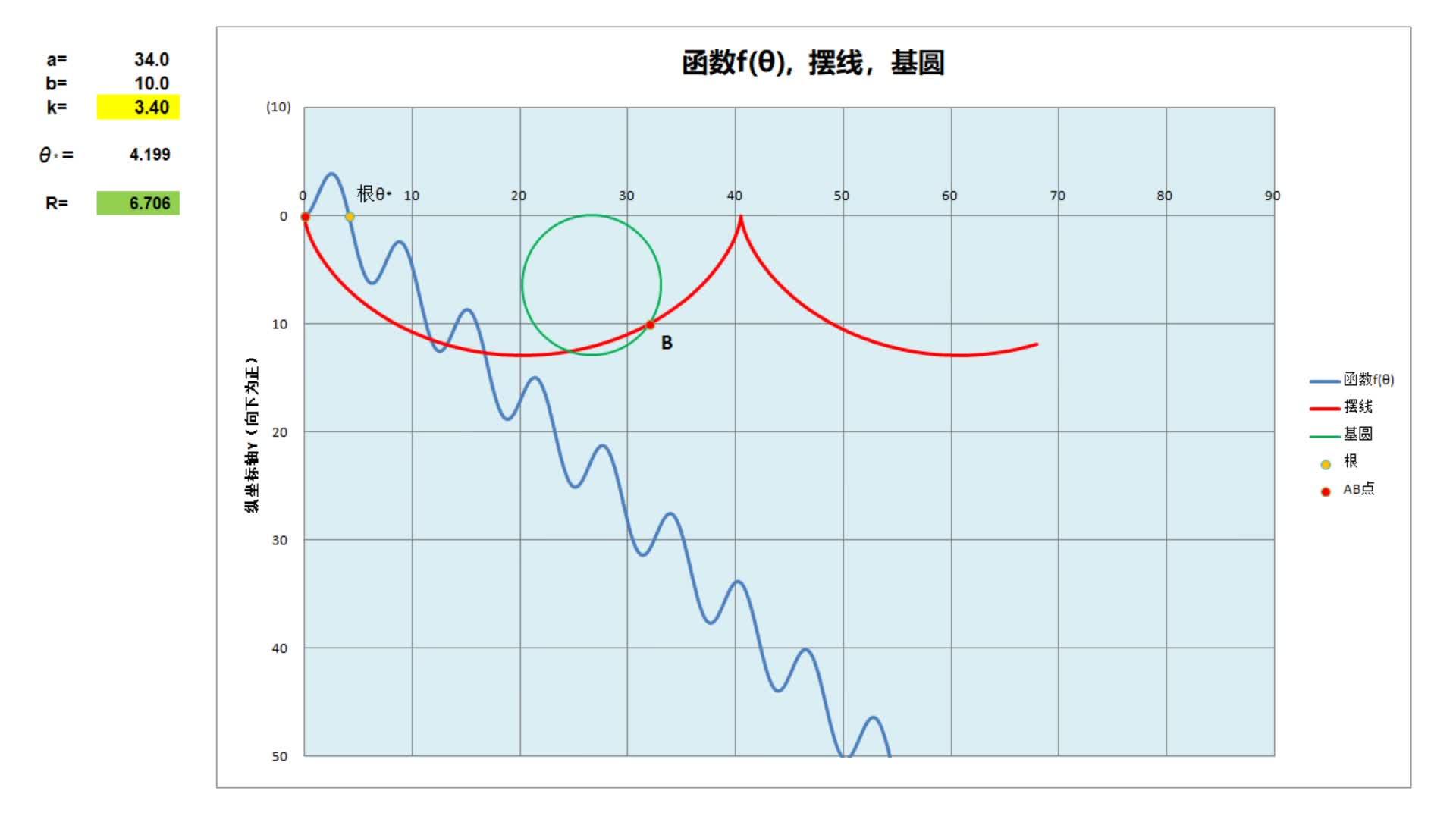
以 b=10 (米)为例,下面视频演示了函数曲线 f(\theta) 对应不同的 k 的表现形态及相应的根 \theta_* 和半径 R 。
 视频1:对应不同 k 的函数动图https://www.zhihu.com/video/1479105947071602689
视频1:对应不同 k 的函数动图https://www.zhihu.com/video/1479105947071602689比较有趣的是,当 k<4.5 时, f(\theta)=0 有唯一的正根, k\geq 4.5 时,有不止一个正根,k 越大,根越多。例如 k=5 时(对应 a=50, b=10 )有三个正根,除了原点,曲线有三次穿越X轴, 对应三个不同的基圆半径,形成三条不同的摆线,如下图,分别用红,绿,黄三种颜色表示,三条摆线都会经过相同点B点 (50,10) 。

那么选取哪个根呢?为了使滑行时间最短,应当取最小的一个根 \theta_* =4.595 ,对应基圆的半径最大,即红色摆线。这在后面分析滑行时间时会明白这一点。我们知道,摆线是周期函数,周期为 2\pi 。在 \theta=\pi 时,处于最低点 (\pi R, 2R) , 宽高比为 \frac{\pi}{2} 。因此,当AB点的宽高比 k >\frac{\pi}{2} 时,质点会越过最低点。当 k 较大时,质点要滑到B点,不但越过最低点,还可能越过最高点 (X轴上的点),在不计空气阻力情况下,在最高点速度降为零,然后再次滑落,以此循环。即便如此,滑行时间依然比沿直线或其他曲线滑行的时间更短,马上阐述这一点。
II:不同曲线的滑行时间比较
设质点沿曲线 y=y(x) 滑行,从A点到曲线上任意一点 (x,y) , 设Y轴朝下为正数。按机械能守恒,有 mgy=\frac12mv^2\Rightarrow v=\sqrt{2gy}\ ,其中 g 为重力加速度。
弧长的微分: ds=\sqrt{(dx)^{2}+(dy)^{2}}=\sqrt{1+y'^2}dx\
因为 v=\frac{ds}{dt}\Rightarrow dt=\frac{ds}{v}\
因此积分得到滑行总时间 T=\int_{0}^{a}\frac{ds}{v}=\int_{0}^{a}\sqrt{\frac{1+y'^2}{2gy}}dx\
使 T 到达最小值的曲线 y(x) 便是最速降线,也就是摆线 (由上面的参数方程描述),网上有许多文章介绍最速降线的求取或证明,这里不再赘述。被积函数是一个泛函, 泛函极值问题的求取促进了变分法学科的诞生。这里侧重研究不同曲线滑行时间的比较。
1. 直线: y=\frac{b}{a}x , x\in[0,a] ,则 y'=\frac{b}{a} , 代入公式,得滑行总时间为:
T_1=\int_{0}^{a}\sqrt{\frac{1+(\frac{b}{a})^2}{2g(\frac{b}{a})x}}dx=\int_{0}^{a}\sqrt{\frac{a^{2}+b^2}{2gabx}}dx=\sqrt{\frac{2(a^{2}+b^2)}{gb}} , (1)
沿直线滑行,路程最短,但时间却并非最短。当 a 趋近 0 时,滑行时间趋近 \sqrt{\frac{2b}{g}} , 这便是沿铅垂线向下的自由落体时间。
2. 摆线:参数方程 \begin{cases} x=R(\theta-\sin\theta)\\[2ex] y=R(1-\cos\theta)\\[2ex] \end{cases}\ \theta\in[0, \theta_{*}]
\theta_* 由上面的提到的数值求根得到。
将滑行时间由 x\in[0,a] 积分转为幅角 \theta\in [0,\theta_{*}] 的积分,注意
ds=\sqrt{(dx)^{2}+(dy)^{2}}=\sqrt{[R(1-cos\theta)d\theta]^{2}+[Rsin\theta d\theta]^{2}}
=R\sqrt{(1-cos\theta)^2+sin^{2}\theta}d\theta=R\sqrt{2-2cos\theta}d\theta ,滑行时间为:
T_2=\int_{0}^{\theta_{*}}\frac{ds}{v}=\int_{0}^{\theta_{*}}\frac{R\sqrt{2-2cos\theta}d\theta}{\sqrt{2gy}}=\int_{0}^{\theta_{*}}\frac{R\sqrt{2-2cos\theta}d\theta}{\sqrt{2gR(1-cos\theta)}}
=\int_{0}^{\theta_{*}}\sqrt{\frac{R}{g}}d\theta=\sqrt{\frac{R}{g}}\theta_{*}
注意 R 是由幅角 \theta_{*} 确定的, R=\frac{b}{1-cos\theta_*} , 因此
T_2=\sqrt{\frac{R}{g}}\theta_{*}=\sqrt{\frac{b}{g(1-cos\theta_*)}}\theta_{*} , (2)
3. 抛物线:请注意,图1选择的几种曲线都有个共同的特点,都是在A点与Y轴相切(直线除外),以便从A点开始,质点能尽快获取更大速度。抛物线选取如下图,经过A,B两点:

抛物线方程: x=\frac{a}{b^{2} }y^{2},y=b\sqrt{\frac{x}{a}},y'=\frac{b}{2\sqrt{ax}} ,滑行时间为:
T_3=\int_{0}^{a}\sqrt{\frac{1+y'^2}{2gy}}dx=\int_{0}^{a}\sqrt{\frac{1+\frac{b^{2}}{4ax}}{2gb\sqrt{\frac{x}{a}}}}dx=\int_{0}^{a}\sqrt{\frac{4ax+b^{2}}{8gbx\sqrt{ax}}}dx
=\int_{0}^{b}\sqrt{\frac{4a(\frac{a}{b^{2} }y^{2})+b^{2}}{8bg(\frac{a}{b^{2} }y^{2})\frac{ay}{b}}}d(\frac{a}{b^{2} }y^{2})=\int_{0}^{b}\sqrt{\frac{4a^2y^{2}+b^{4}}{8ga^2y^3}}\frac{2a}{b^{2} }ydy
=\frac{1}{\sqrt{2g}}\int_{0}^{b}\sqrt{\frac{4a^2y^{2}+b^{4}}{b^4y}}dy (换元: y=z^2 )
=\frac{1}{\sqrt{2g}}\int_{0}^{\sqrt{b}}\sqrt{\frac{4a^2z^2}{b^4}+\frac{1}{z^2}}d(z^2)=\sqrt{\frac{2}{g}}\int_{0}^{\sqrt{b}}\sqrt{1+(\frac{\sqrt{2a}}{b}z)^4}dz
再换元: t=\frac{\sqrt{2a}}{b}z ,得
T_3=\frac{b}{\sqrt{ag}}\int_{0}^{\sqrt{\frac{2a}{b}}}\sqrt{1+t^4}dt , (3)
这个定积分比较难积,可用数值积分法(如复合型T型公式或Simpson公式)获得数值解。
4. 椭圆:标准方程: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 , 如下图,截取当中 A 到 B 的部分 (第三象限)。
参数方程为: \begin{cases} x=acos\varphi\\[2ex] y=bsin\varphi\\[2ex] \end{cases}\ \varphi\in[\pi,\frac{3\pi}{2}]

将椭圆中心由原点移至 (a,0) , 则 A点变为坐标原点 (0,0) , 令: \varphi=\theta+\pi 其中 \theta\in[0,\frac{\pi}{2}] ,则适用图1的椭圆参数方程为: \begin{cases} x=-acos\theta+a\\[2ex] y=bsin\theta\\[2ex] \end{cases}\ \theta\in[0,\frac{\pi}{2}]
将滑行时间的积分由 x\in[0,a] 积分转为 幅角 \theta\in [0,\frac{\pi}{2}] 的积分,注意
ds=\sqrt{(dx)^{2}+(dy)^{2}}=\sqrt{(asin\theta d\theta)^{2}+(bcos\theta d\theta)^{2}}
=\sqrt{a^2sin^2\theta+b^2cos^{2}\theta}d\theta ,滑行时间为:
T_4=\int_{0}^{\frac{\pi}{2}}\frac{ds}{v}=\int_{0}^{\frac{\pi}{2}}\frac{\sqrt{a^2sin^2\theta+b^2cos^{2}\theta}d\theta}{\sqrt{2gbsin\theta}} ,即
T_4=\frac{1}{\sqrt{2gb}}\int_{0}^{\frac{\pi}{2}}\sqrt{(a^2-b^2)sin\theta+\frac{b^2}{sin\theta}}d\theta , (4)
这个积分可以采用数值积分法求解。注意积分函数第二项当 \theta \rightarrow 0 时, \frac{b^2}{sin\theta}\rightarrow \infty ,但积分是存在的,不会无穷大。记 c=\frac{a^2-b^2}{b^2} , 设 \varepsilon 为充分小的的量,则:
T_4=\sqrt{\frac{b}{2g}}\int_{0}^{\varepsilon}\sqrt{csin\theta+\frac{1}{sin\theta}}d\theta+\sqrt{\frac{b}{2g}}\int_{\varepsilon}^{\frac{\pi}{2}}\sqrt{csin\theta+\frac{1}{sin\theta}}d\theta
=\sqrt{\frac{b}{2g}}(I_1+I_2)
I_1\approx\int_{0}^{\varepsilon}\sqrt{c\theta+\frac{1}{\theta}}d\theta =\int_{0}^{\sqrt{\varepsilon}}\sqrt{ct^2+\frac{1}{t^2}}d(t^2)=2\int_{0}^{\sqrt{\varepsilon}}\sqrt{ct^4+1}dt
\approx2\int_{0}^{\sqrt{\varepsilon}}(1+\frac{c}{2}t^4)dt=2\sqrt{\varepsilon}+\frac{c}{5}\varepsilon^{2.5} \rightarrow 0 (当 \varepsilon\rightarrow 0 ) 。
因此 T_4 的积分存在,按给定精度要求,可取充分小的量 \varepsilon 在区间 [\varepsilon, \frac{\pi}{2}] 积分就可。
5. 圆弧线:这是伽利略曾经认为的最速曲线(其判断是错的)。经过AB两点的圆弧有无数个,如何选取最佳的圆弧使得滑行时间在所有圆弧中最短?设直线AB中点为D点,经D点作AB的中垂线交X轴与E点,以E点为圆心,EA为半径作圆弧,则 |EA|=|EB|。该圆弧在A点与Y轴相切,从而使质点从A滑落能尽快取得垂直方向加速度,如下图的绿色圆弧:

D点坐标 (x_d,y_d)=(\frac{a}{2}, \frac{b}{2}) , AB直线方程: y=\frac{1}{k}x (其中 k=\frac{a}{b} 为宽高比)。中垂线的方程: y-\frac{b}{2}=-k(x-\frac{a}{2}) , 令 y=0 得E点坐标 (x_e,y_e)=(\frac{a^2+b^2}{2a}, 0) , 圆半径 : r=|AE|=\frac{a^2+b^2}{2a} , 圆方程: (x-x_e)^2+y^2=r^2
圆弧从A点到B点,A点弧度 \varphi_{a}=0 ,B点弧度 \varphi_{b} 为:
\varphi_{b}=\begin{cases} arctan\frac{2ab}{|a^2-b^2|} , k<1\\[2ex] \pi-arctan\frac{2ab}{|a^2-b^2|}, k>1\\[2ex] \frac{\pi}{2}, k=1 \end{cases}\
圆弧的参数方程: \begin{cases} x=-rcos\theta+r\\[2ex] y=rsin\theta\\[2ex] \end{cases}\ \theta\in[0,\varphi_{b}]
ds=\sqrt{(dx)^{2}+(dy)^{2}}=\sqrt{(-rsin\theta d\theta)^{2}+(rcos\theta d\theta)^{2}}=rd\theta
由此得滑行时间为:
T_5=\int_{0}^{\varphi_{b}}\frac{ds}{\sqrt{2gy}}=\int_{0}^{\varphi_{b}}\frac{rd\theta}{\sqrt{2grsin\theta}} ,即
T_5=\sqrt{\frac{r}{2g}}\int_{0}^{\varphi_{b}}\frac{d\theta}{\sqrt{sin\theta}} , (5)
同椭圆的情况类似,被积函数当 \theta \rightarrow 0 时, \frac{1}{\sqrt{sin\theta}}\rightarrow \infty ,但积分是存在的, 不会无穷大。
设 \varepsilon 为充分小的的量,则 I=\int_{0}^{\varepsilon}\frac{d\theta}{\sqrt{sin\theta}}\approx\int_{0}^{\varepsilon}\frac{d\theta}{\sqrt{\theta}}=2\sqrt{\varepsilon}\rightarrow 0 (当 \varepsilon\rightarrow 0 ) 。
因此 T_5 的积分存在,按给定精度要求,可取充分小的 \varepsilon 在区间 [\varepsilon, \frac{\pi}{2}] 进行数值积分。
有了这几种曲线的计算公式或积分公式,便可进行滑行时间的比较。
以下是以 b=10 (米) 为例,k 取不同值计算的滑行时间数据 (单位秒,精确到毫秒):

由此看出,对给定的 B 点坐标 (a,b) , 各曲线的滑落时间不同: 无论 k 取值如何,摆线时间总是最短,是最速降线。沿直线滑落,距离最短,时间却最长。k较小时,沿各曲线的滑落时间相差不大,k较大时,比如 k=8,时间差距拉大,摆线时间只有直线时间的一半左右 (50.6%),圆弧线的路径最长,时间第二短,为直线时间的(53%). 沿抛物线和椭圆滑落要花更多时间,分别为直线时间的69.6%和63.8%。
以上是质点沿各曲线滑到 B 点的总时间。类似地,对给定的 B 点而相应确定的各曲线,质点在曲线上任意坐标点的时间可以算出,有类似公式:
直线: T_1(x)=\sqrt{\frac{2(a^{2}+b^2)x}{gab}} ,x\in[0,a]
摆线: T_2(\theta)=\sqrt{\frac{R}{g}}\theta , \theta\in[0,\theta_*]
其中 \theta_* 是 f(\theta)=0 的根, R=\frac{b}{1-cos\theta_*} 。
抛物线: T_3(y)=\frac{b}{\sqrt{ag}}\int_{0}^{\sqrt{\frac{2y}{b^2}}}\sqrt{1+t^4}dt , y\in [0,b]
椭圆: T_4(\varphi)=\frac{1}{\sqrt{2gb}}\int_{0^{+}}^{\varphi}\sqrt{(a^2-b^2)sin\theta+\frac{b^2}{sin\theta}}d\theta , \varphi \in(0, \frac{\pi}{2}]
圆弧: T_5(\varphi)=\sqrt{\frac{r}{2g}}\int_{0^+}^{\varphi}\frac{d\theta}{\sqrt{sin\theta}} , \varphi \in(0, \varphi_b]
这是以坐标点(横坐标,或纵坐标,或幅角) 为自变量的时间函数。
III:相同时间质点在曲线上的位置。
如果以时间为自变量,如何确定质点在各曲线上的坐标点?那就是时间函数的反函数,直接求取比较困难 (直线和摆线容易求出,抛物线,椭圆和圆弧非常困难),可以采用函数插值的方法获取数值解。这样便得到在任意时间点,质点在各曲线上的位置。当时间连续变化,就得到质点沿曲线滑落的动态图。下面视频演示了按时间变量的精确位置的动图(以k=2 和 k=8为例)。
 https://www.zhihu.com/video/1480307759246110720
https://www.zhihu.com/video/1480307759246110720该视频显示,k=8时,沿摆线和圆弧线滑落要快许多,将沿直线前行的质点远远甩在后面,非常有趣。
