微积分入门——积分入门
我们知道如何计算像是三角形、矩形、圆形这样简单图形的面积
但是我们如何计算抛物线所包围的区域面积呢?

面积问题
古代几何学家思考过这个问题,但微积分的发明才完全解答了这个问题。让我们一步一步地完成这个过程。
首先,我们通过将抛物线拟合到矩形内来找到抛物线面积的上限:

图中面积上限是?
- \frac18
- \frac14
- \frac12
- 1
解答:
矩形高度为0.25=1/4,底边长度为1,所以面积为1/4x1=1/4
因为抛物线在矩形里面,其面积肯定小于1/4
现在,我们能使用该上限作为抛物线面积的估计值,但它会是一个很好的估计值吗? 不
是的! 看,矩形的面积包括抛物线以外的所有空间,所以 1/4高估了抛物线的面积。
让我们尝试用两个矩形做得更好。
要了解我们如何选择这些新矩形,我们需要重新考虑我们如何选择第一个矩形。
从表面上看,这个矩形是唯一一个底边完全沿着抛物线域
y=f(x)=x(1−x),0≤x≤1\\
且高度与下方抛物线完美契合:

换一种方式看,它是一个矩形,其底边沿区间 [0,1] ,高度通过评估中点 f 给出:
f\left( \frac{1}{2} \right) = \frac{1}{2} \left( 1- \frac{1}{2} \right) = \frac{1}{4} .\\
假设我们为 f(x) = x(1-x) 选择一个新矩形,其底边等于区间 \left[ 0, \frac12\right] ,高度由区间中点给出
矩形高度为多少?
- \frac1{16}
- \frac3{16}
- \frac12
- \frac9{16}
解答:
区间 \left[ 0, \frac12\right] 的中点为 \frac14 ,所以矩形高度为
\begin{aligned} f\left( \frac{1}{4} \right) & = \frac{1}{4} \left( 1- \frac{1}{4} \right) \\ & = \frac{1}{4} \times \frac{3}{4} \\& = \frac{3}{16}. \end{aligned}\\
现在,以另一个区间为底的矩形 \left[\frac12 ,1 \right] 具有相同的高度,所以如果我们在同一个图上将它们绘制在一起,我们会得到:

期待抛物线外的阴影区域大致等于其下方和两个矩形上方的空白区域。
两个矩形的组合面积为我们提供了对抛物线面积更好的估计。
现在,两个矩形的总面积为多少?
- \frac3{32}
- \frac3{16}
- \frac38
- \frac34
解答:
两个矩形具有相同的高度和相同的底长,因此我们只需将一个的面积加倍即可获得总面积
底边长度为\frac12 而高度是 \frac3{16} ,正如我们之前发现的那样。将这些相乘得到单个矩形的面积\frac3{32}
将其加倍得到总面积 \frac3{16}
我们的最初估计从使用一个矩形的 \frac14 = 0.25 下降到使用两个矩形的 \frac3{16} = 0.1875 。
仅使用一个矩形会大大超出真实区域,因此使用两个矩形进行较小的估计是朝着正确方向迈出的一步。
如果我们使用越来越多的矩形,我们应该得到越来越好的估计:
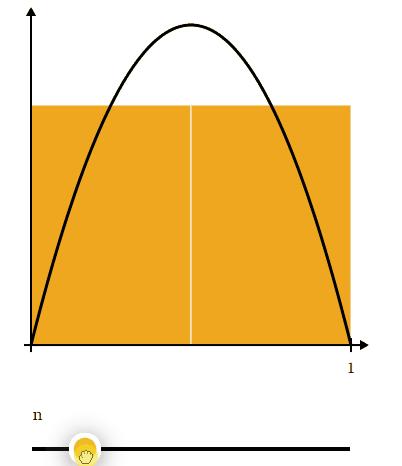
很容易说我们可以通过使用无限多的矩形来获得抛物线面积的确切值。
但是实际上是否可以使用无限数量的矩形?猜到这里就OK了。
【是】【否】
不错的猜测,但实际上是不可能的!
让我们看看如果我们尝试使用无限数量的矩形来找到抛物线的面积,我们会遇到什么麻烦。
假设我们尝试沿着区间 [0,1] 拟合 n 个底边长度为 b 的矩形。
底边长度 b 是随 n 上升还是下降?
【上升】【下降】
没错!
如果我们在下图中向上拨 n,矩形会变窄:

更精确地说,由于 n 个底边长度为 b 的矩形必须完全符合区间 [0,1], nb=1 。
这是因为区间 [ 0, 1 ] 本身的长度为 1
重新排列,我们得到 b = \frac{1}{n} ,b 随着 n 的上升而下降。
因此,如果我们从字面上使用无限数量的矩形,这些“矩形”的底长将为 0,没有面积。
那么,这整个尝试使用矩形获得抛物线面积的确切值是否是一个死胡同呢?
一点也不。我们可以借助称为极限的微积分概念来保存它。
如果我们使用有限数量的矩形,比如 n,那么我们可得到 \frac{1}{6} + \frac{1}{12 n^2} 作为抛物线面积的估计
我们不需要获取抛物线面积估计值的详细信息,但如果您有兴趣,请继续阅读。否则,请随时跳过。
如果我们使用 n 个矩形,那么底边长度为 \frac1n 。
所以矩形底边位于子区间 \left [ 0, \frac{1}{n} \right], \left[ \frac{1}{n}, \frac{2}{n} \right] , \dots , \left [\frac{n-1}{n},1 \right] 上,底边中点为
\begin{aligned} \frac{0+\frac1n}{2} & = \frac{1}{2n}, \\ \frac{\frac1n + \frac2n}{2} & = \frac{3}{2n} , \\ &\ \ \vdots \\ \frac{\frac{n-1}n + 1}{2} & = \frac{n-\frac12}{n}. \end{aligned}\\
让我们用整数 j 标记每个子区间,即 j=1标记为 \left[ 0, \frac1n\right] ,j=2标记为 \left[ \frac1n, \frac2n\right],依此类推。
这意味着区间 j 的中点为 \frac{j-\frac12}{n} = \frac{2j -1}{2n}. 试着亲自插入一些 j 值来测试它看看是否有效。
矩形 j 的高度为 \begin{aligned} f \left( \frac{2j -1}{2n} \right) & = \frac{2j -1}{2n} \left( 1 - \frac{2j -1}{2n} \right) \\ & = \frac{2j -1}{2n} \times \frac{2n + 1 - 2j}{2n} \\ & = \frac{(2j-1)(2n+1 - 2j)}{4 n^2}, \end{aligned}\\
底边为 \frac1n
所以矩形 j 的面积为 \frac{(2j-1)(2n+1 - 2j)}{4 n^3} = \frac{ 4(n+1) j - 4 j^2 -(2n+1)}{4 n^3}.
为了得到我们的估计,我们必须将所有这些区域相加,从 j = 1 开始,到 j = n 结束。
有两个公式在这儿可以帮助我们:
1 + 2 + 3 + \dots + n = \frac{n(n+1)}{2} 和 1^2 + 2^2 + 3^2 + \dots + n^2 = \frac{n (n+1) (2 n+1)}{6}.
这些恒等式告诉我们所有矩形面积之和等于 \frac{4 (n+1) \times \frac{n(n+1)}2 - 4 \times \frac{ n (n+1) (2 n+1)}6 - (2n+1)\times n }{4n^3}
简化后如下 \frac{1}{6} + \frac{1}{12 n^2}.
哇!
如果我们认为 n 非常非常大(但有限),这个估计值是多少?
- \frac1{12}
- \frac16
- \frac13
- \frac12
解答:
当 n 非常非常大时, 12 n^2 非常大,表示 1/(12n^2) 非常小。
所以 \frac{1}{6} + \frac{1}{12 n^2} 中的第二项非常小到可以忽略
换句话说,估计值将近 \frac16
当n趋近于无限,我们可以估计面积 \frac{1}{6} + \frac{1}{12 n^2} 也趋近于极限 \frac16
一个更简便的表示法是: \lim\limits_{ n \to \infty} \left( \frac{1}{6} + \frac{1}{12 n^2} \right) = \frac{1}{6}.
这就是微积分教会我们如何得到抛物线面积的精确值 \frac16 = 0.16\dots
我们并不是从字面上对无限数量的矩形求和——当矩形的数量接近无穷大时,我们会查看和的极限。

由于我们将很多分开的矩形的区域积累或整合在一起,我们将得到的区域称为积分。
我们使用拉长的“s”(s 表示“sum”)来表示积分。例如,对于抛物线,我们写成
\int\limits_{0}^{1} x(1-x)\,dx = \frac{1}{6}.\\
如果这些符号的部分或全部还没有意义,请不要担心——我们将在课程的后面部分详细介绍。
现在,让我们看一下积分可以用来做的一些事情
应用
加百列号角
例如,如果我们绕 x 轴进入第三维旋转 f(x) = \frac1x , x\geq1 的图像,我们得到一个称为加百列号角的形状:

它的表面积,我们可以认为是完全涂满其外部所需的涂料量,
即 2\pi f(x) \sqrt{1+\big[f'(x) \big]^2 } 在 f(x)= \frac1x 时的积分。
我们将在课程的稍后部分展示并计算它。
号角永远延伸,下图只显示了 x = 1 和 x = l+1 之间的部分,其表面积 SA 服从
\text{SA}(l) > 2\pi \ln(l + 1): \\

当 l 变大时,你注意到表面积是怎样的?
【保持不变】【收缩】【继续扩大】
非常正确! 表面积与\ln(l+1)成正比,其中 l 是我们可以看到的号角部分的长度。
如果我们一直向上调动 l,我们会看到表面积变得非常大。
事实上,对数函数会不断增长,所以加百列号角的总面积不可能是有限的。
换句话说,没有办法用有限的涂料给号角上色。这符合我们的直觉,因为号角是无限长的。
现在,假设我们要计算加百列号角的体积而不是其表面积。
正如我们稍后将在课程中看到的,总体积等于 \pi \big[ f(x) \big]^2 = \frac{\pi}{x^2} 的积分
在 x = 1 和 x=l+1 之间的号角部分的体积是 V(l)=\pi \left( 1 - \frac{1}{l+1} \right):

随着长度 l 的增加,它的体积是怎样的?
【保持不变】【收缩】【继续扩大】
非常正确!
就像我们对表面积所做的那样,我们将 l 一直向上拨动,以查看当我们看到越来越多的号角时体积的表现。
令人惊讶的是,体积量趋向于 \pi = 3.14159\ldots
积分显示加百列号角是多么奇怪:
即使它永远延伸并且我们永远无法完全涂满它的外部,我们却可以用有限数量的涂料填满它!
运动(物理学)
计算面积和体积并不是积分的唯一用途——它们还可以帮助我们解决运动问题。
在上一课中,我们发现炮弹的速度 v(t) 等于 h'(t),即高度函数 h(t) 的导数。

事实证明,v(t) 的积分为我们提供了炮弹的位移[1]: h(b)-h(a) = \int\limits_{a}^{b} v(t)\, dt.
在这里,t = a 是我们开始关注炮弹的时间,t = b 是我们停止的时间。我们将在课程后面说明为什么这是真的
考虑到上面说的一切,积分 \int\limits_{0}^{2} v(t)\, dt = \int\limits_{0}^{2} ( 10 - 10t )\, dt 等于?(提示:不要考虑积分怎么计算)
- 0
- 2
- 5
- 7
解答:0
我们可以通过一个个的矩形进行面积求和来从头开始计算积分,但是h(2)-h(0) = \int\limits_{0}^{2} v(t)\, dt 直接给了我们一条捷径——因为炮弹在同一高度开始和停止, \begin{aligned} h(2)- h(0) &= 2 - 2 \\ &= 0 \\ &= \int\limits_{0}^{2} v(t)\, dt \\ &= \int\limits_{0}^{2} \left( 10 - 10t \right )\, dt. \end{aligned}
这实际上是一个更深层次结果的示例,称为微积分的基本定理:
f(b) - f(a) = \int\limits_{a}^{b} f'(x)\, dx.\\
记住,f ' 是 f 的导数
我们将在课程后面证明它并用它来计算复杂的积分。
回顾和反思
我们将积分介绍为由函数图像界定的区域的面积,但它的用途远远超出几何:
积分可以在运动、工程、概率和统计中找到。
我们将研究其中一些积分的应用,并在我们的课程后面开发更清晰的工具来计算它们。
结束
参考
- ^位移是指一个物体位置的整体变化

