David Silver 增强学习补充知识——梯度下降法

前言

本文是《David Silver 增强学习》（后5章）的补充知识，帮助大家理解梯度下降算法。

虽然在Tensorflow中一行代码就能实现不同的梯度下降算法，但还是希望大家能够从数学角度去认识它们。

这样能够帮助我们在调参时有一个明确的思路。

目录

1.1 导数
1.2 微分
1.3 偏导数
1.3.1 偏导数的几何意义
1.4 方向导数
1.4.1 定理
1.5 梯度
1.5.1 示例 \frac{x}{e^{ x^2+y^2}}

2.1 梯度下降法
2.1.1 示例——单变量函数的梯度下降 J\left( \theta \right)=\theta^2
2.1.2 示例——多变量函数的梯度下降 J\left( \theta \right)=\theta^2_1+\theta^2_2
2.1.3 示例——线形回归

3.1 梯度下降法变体1——批量梯度下降法（Batch gradient descent，BGD）
3.2 梯度下降法变体2——随机梯度下降法（Stochastic Gradient Descent，SGD）
3.3 梯度下降法变体3——小批量梯度下降法（Mini-batch Gradient Descent，MBGD）

4.1 指数加权移动平均（Exponential Weighted Moving Average）
4.1.1 加权平均VS算术平均
4.1.2 指数加权移动平均
4.1.3 指数加权平均实现
4.1.4 指数加权平均的偏差修正

5.1 梯度下降优化算法1——动量梯度下降法
5.1.1 算法实践
5.1.2 TensorFlow中提供了动量梯度下降算法的实现
5.1.3 示例

6.1 Nesterov加速梯度法
6.1.1 TensorFlow中的NAG优化器
6.1.2 示例

7.1 Adagrad法
7.1.1 TensorFlow中的Adagrad优化器
7.1.2 示例

8.1 Adadelta法
8.1.1 TensorFlow中的Adadelta优化器
8.1.2 示例

9.1 RMSprop
9.1.1 TensorFlow中的RMSprop优化器
9.1.2 示例

10.1 适应性动量估计法（Adaptive Moment Estimation，Adam）
10.1.1 TensorFlow中的Adam优化器
10.1.2 示例

11.1 学习速率 \alpha

12.1 如何选择合适的优化算法

1.1 导数

设函数 y=f\left( x \right) 在 x_0 的某领域内有定义，当自变量从 x_0 变到 x_0+\Delta x 时，函数 y=f\left( x \right) 的增量 \Delta y=f\left( x_0+\Delta x \right)-f\left( x_0 \right) 与自变量的增量 \Delta x 之比 \frac{\Delta y}{\Delta x}=\frac{f\left( x_0+\Delta x \right)-f\left( x_0 \right)}{\Delta x} 称为 f\left( x \right) 的平均变化率。如果 \Delta x \rightarrow 0 时，平均变化率的极限 \mathop{\textrm{lim}}_{\Delta x \rightarrow 0}\frac{\Delta y}{\Delta x}=\mathop{\textrm{lim}}_{\Delta x \rightarrow 0}\frac{f\left( x_0+\Delta x \right)-f\left( x_0 \right)}{\Delta x} 存在，则称 f\left( x \right) 在 x_0 处可导，并称此极限值为函数 f\left( x \right) 在 x_0 处的导数，用记号 y'{\Big |}_{x=x_0} 、 f'\left( x_0 \right) 、 \frac{\mathrm{d}y}{\mathrm{d}x}{\Big |}_{x=x_0} 或 \frac{\mathrm{d}f}{\mathrm{d}x}{\Big |}_{x=x_0} 表示。

导数 f'\left( x \right) 也代表 f\left( x \right) 在点 x 处的斜率。导数对于最小化一个函数很有用，因为它告诉我们如何更改 x 来略微地改善 y 。

当 f'\left( x \right)=0 ，导数无法提供往哪个方向移动的信息。 f'\left( x \right)=0 的点称为临界点（critical point）或驻点（stationary point）。一个局部极小点（local minimum）意味着这个点的 f\left( x \right) 小于所有邻近点，因此不可能通过移动无穷小的步长来减小 f (x) 。一个局部极大点（local maximum）意味着这个点的 f (x) 大于所有邻近点，因此不可能通过移动无穷小的步长来增大 f(x) 。有些临界点既不是最小点也不是最大点。这些点被称为鞍点（saddle point）。下图给出了各种临界点的例子。

使 f(x) 取得绝对的最小值（相对所有其他值）的点是全局最小点（global minimum）。函数可能只有一个全局最小点或存在多个全局最小点，还可能存在不是全局最优的局部极小点。在深度学习的背景下，我们要优化的函数可能含有许多不是最优的局部极小点，或者还有很多处于非常平坦的区域内的鞍点。尤其是当输入是多维的时候，所有这些都将使优化变得困难。因此，我们通常寻找使 f 非常小的点，但这在任何形式意义下并不一定是最小。见下图的例子。

1.2 微分

设函数 y=f\left( x \right) 在 x 附近有定义，若自变量从 x_0 变到 x_0+\Delta x 时，函数的增量可表示为 \Delta y=A \Delta x+o\left( \Delta x \right) 的形式，其中 A 与 \Delta x 无关，则说函数 f\left( x \right) 在 x 处可微，并把 A\Delta x 称为函数 f\left( x \right) 在 x 处的微分，记为 {\mathrm d}y 或 {\mathrm d}f\left( x \right) ，即 {\mathrm d}y=A \Delta x 。

1.3 偏导数

设函数 z=f\left( x,y \right) 在点 \left( x_0,y_0 \right) 的某临域内有定义，固定 y=y_0 ，给 x_0 以增量 \Delta x ，称 \Delta_xz=f\left( x_0+\Delta x,y_0 \right)-f\left( x_0,y_0 \right) 为 f\left( x,y \right) 在点 \left( x_0,y_0 \right) 处关于 x 的偏增量。若极限 \mathop{\textrm{lim}}_{\Delta x \rightarrow 0}\frac{\Delta_xz}{\Delta x}=\mathop{\textrm{lim}}_{\Delta x \rightarrow 0}\frac{f\left( x_0+\Delta x,y_0 \right)-f\left( x_0,y_0 \right)}{\Delta x} 存在，则称此极限值为函数 z=f\left( x,y \right) 在点 \left( x_0,y_0 \right) 处关于 x 的偏导数，记为 \frac{\partial z}{\partial x}{\Big |}_{\left( x_0,y_0 \right)} 或者 f'_x\left( x_0,y_0 \right) 。同样定义函数 z=f\left( x,y \right) 在点 \left( x_0,y_0 \right) 处关于 y 的偏导数为 \frac{\partial z}{\partial y}{\Big |}_{\left( x_0,y_0 \right)}=f'_y\left( x_0,y_0 \right)=\mathop{\textrm{lim}}_{\Delta y \rightarrow 0}\frac{\Delta_yz}{\Delta y}=\mathop{\textrm{lim}}_{\Delta y \rightarrow 0}\frac{f\left( x_0,y_0+\Delta y \right)-f\left( x_0,y_0 \right)}{\Delta y} 。

• 1.3.1 偏导数的几何意义

因为偏导数 f'_x\left( x_0,y_0 \right) 就是一元函数 f\left( x_0,y_0 \right) 在 x_0 处的导数，所以几何上 f'_x\left( x_0,y_0 \right) 表示曲面 z=f\left( x,y \right) 与平面 y=y_0 的交线 z=f\left( x,y_0 \right) 在点 \left( x_0,y_0,f\left( x_0,y_0 \right) \right) 处的切线对 x 轴的斜率。同样 f'_y\left( x_0,y_0 \right) 表示曲面 z=f\left( x,y \right) 与平面 x=x_0 的交线 z=f\left( x_0,y \right) 在点 \left( x_0,y_0,f\left( x_0,y_0 \right) \right) 处的切线对 y 轴的斜率。

1.4 方向导数

设点 P_0 \in D ， l 是从 P_0 引出的射线， \vec{l} 为其方向向量。在 l 上取一临近点 P_0 的动点 P ，记 \left| P_0P \right|=\rho ，如果当 P \mathop{\rightarrow}^{l} P_0 时，比式 \frac{\Delta u}{\rho}=\frac{u\left( P \right)-u\left( P_0 \right)}{\left| PP_0 \right|} 的极限存在，则称此极限为函数 u=u\left( P \right) 在点 P_0 处沿 \vec l 方向的方向导数，记为 \frac{\partial u}{\partial \vec l}{\Big |}_{P_0} ，即 \frac{\partial u}{\partial \vec l}{\Big |}_{P_0}=\mathop{\textrm{lim}}_{\rho \rightarrow 0}\frac{\Delta u}{\rho}=\mathop{\textrm{lim}}_{P \rightarrow P_0}\frac{u\left( P \right)-u\left( P_0 \right)}{\left| PP_0 \right|} 。

方向导数是函数 u=u\left( P \right) 沿指定方向对距离 \rho 的变换率，当 \frac{\partial u}{\partial \vec l}{\Big |}_{P_0}>0 时，函数 u 在 P_0 处沿 \vec l 方向是增加的；当 \frac{\partial u}{\partial \vec l}{\Big |}_{P_0}<0 时，函数 u 在 P_0 处沿 \vec l 方向是减小的。

• 1.4.1 定理

设 u=u\left( x,y,z \right) 在点 P_0\left( x_0,y_0,z_0 \right) 处可微，则函数 u\left( x,y,z \right) 在点 P_0 处沿任意指定方向 \vec l 的方向导数都存在，且 \frac{\partial u}{\partial \vec l}{\Big |}_{P_0}=\frac{\partial u}{\partial x}{\Big |}_{P_0}\mathrm{cos}\alpha+\frac{\partial u}{\partial y}{\Big |}_{P_0}\mathrm{cos}\beta+\frac{\partial u}{\partial z}{\Big |}_{P_0}\mathrm{cos}\gamma ，其中 \mathrm{cos}\alpha 、 \mathrm{cos}\beta 、 \mathrm{cos}\gamma 是 \vec l 的方向余弦。

1.5 梯度

函数 u\left( P \right) 在点 P 处的梯度是个向量，其方向为 u\left( P \right) 在点 P 的变化率最大的方向，其模恰好等于这个最大的变化率，表达式为 \nabla u={\mathrm{\textbf{grad}}}u=\frac{\partial u}{\partial x}{\textbf{i}}+\frac{\partial u}{\partial x}{\textbf{j}}+\frac{\partial u}{\partial x}{\textbf{k}} 。

• 1.5.1 示例 \frac{x}{e^{ x^2+y^2}}

clear all;clc;
x=linspace(-2, 2, 25);
y=linspace(-2, 2, 25);
[xx,yy]=meshgrid(x,y);
zz=xx.*exp(-xx.^2 - yy.^2);
figure(1);%曲面图
mesh(xx,yy,zz);
colorbar;
print -djpeg -r300 jpg1
%-djpeg是格式,d表示device,jpeg是格式
%-r300表示像素300dpi,r表示resolution,也就是分辨率的第一个字母
%jpg1是文件名
figure(2);%等高线
[C,h] = contour(zz,20);
set(h,'ShowText','off');
axis off;
print -djpeg -r600 jpg2
figure(3);%梯度图
h=contour(zz,20);
[dx, dy]=gradient(zz,.2,2);
hold on;
quiver(dx, dy);
axis off;
print -djpeg -r600 jpg3

2.1 梯度下降法

沿着梯度向量 \left( \frac{\partial u}{\partial x},\frac{\partial u}{\partial y},\frac{\partial u}{\partial z} \right) 的方向，更容易找到函数的最大值；沿着梯度向量 \left( \frac{\partial u}{\partial x},\frac{\partial u}{\partial y},\frac{\partial u}{\partial z} \right) 相反的方向，梯度减少最快，也就更加容易找到函数的最小值。

参数更新公式如下：

\theta\leftarrow \theta-\alpha \cdot \nabla J(\theta)

其中 J(\theta) 是目标函数， \nabla J(\theta) 是 J\left( \theta \right) 关于参数 \theta 的梯度，步长 \alpha 又称为学习速率（通过 \alpha 来控制每一步走的距离，保证不要走太快错过最低点，同时保证不要走太慢导致迟迟走不到最低点）。

• 2.1.1 示例——单变量函数的梯度下降 J\left( \theta \right)=\theta^2

J'\left( \theta \right)=2\theta
\alpha=0.4

\theta^0=1

\theta^1=\theta^0-\alpha \ast J'(\theta^0)=1-0.4\ast 2=0.2

\theta^2=\theta^1-\alpha \ast J'(\theta^1)=0.2-0.4\ast \left( 2\ast0.2 \right)=0.04

\theta^3=\theta^2-\alpha \ast J'(\theta^2)=0.04-0.4\ast \left( 2\ast0.04 \right)=0.008

\theta^4=\theta^3-\alpha \ast J'(\theta^3)=0.008-0.4\ast \left( 2\ast0.008 \right)=0.0016

clear all;clc;
theta0 = 1;alpha = 0.4;
theta=-1:0.01:1;
y=theta.^2;
figure(1);
plot(theta,y,'b-','Linewidth',2);
hold on;
syms Theta Y
Y=Theta^2;
df=diff(Y);
Theta=theta0;
for i=1:4
    plot(Theta,Theta^2,'r*','Linewidth',2);
    hold on;
    Theta=Theta-alpha*eval(df);
end
print -djpeg -r300 example1

• 2.1.2 示例——多变量函数的梯度下降 J\left( \theta \right)=\theta^2_1+\theta^2_2

\nabla J(\theta)=\left( 2\theta_1,2\theta_2 \right)

\alpha=0.1

\theta^0=\left( 1,3 \right)

\theta^1=\theta^0-\alpha\ast\nabla J(\theta)=\left( 1,3 \right)-0.1\ast\left( 2\theta_1,2\theta_2 \right)=\left( 1,3 \right)-0.1\ast\left( 2,6 \right)=\left( 0.8,2.4 \right)

\theta^2=\theta^1-\alpha\ast\nabla J(\theta)=\left( 0.8,2.4 \right)-0.1\ast\left( 2\theta_1,2\theta_2 \right)=\left( 0.8,2.4 \right)-0.1\ast\left( 1.6,4.8 \right)=\left( 0.64,1.92 \right)

clear all;clc;
theta0 = [1,3];alpha = 0.1;
theta_1=-5:0.5:5;
theta_2=-5:0.5:5;
[theta_1_1,theta_2_2]=meshgrid(theta_1,theta_2);
y=theta_1_1.^2+theta_2_2.^2;
figure(1);
mesh(theta_1_1,theta_2_2,y);
hold on;
syms Theta_1 Theta_2 Y
Y=Theta_1^2+Theta_2^2;
df_Theta1=diff(Y,Theta_1);
df_Theta2=diff(Y,Theta_2);
Theta_1=theta0(1);
Theta_2=theta0(2);
Theta=[Theta_1,Theta_2];
for i=1:10
    plot3(Theta_1,Theta_2,eval(Y),'r*','Linewidth',1) 
    hold on;
    Theta=[Theta_1-alpha*eval(df_Theta1),Theta_2-alpha*eval(df_Theta2)]
    Theta_1=Theta(1);
    Theta_2=Theta(2);
end

迭代10次：

Theta =
    0.1074    0.3221

迭代100次：

Theta =
   1.0e-09 *
    0.2037    0.6111

• 2.1.3 示例——线形回归

设 h_{\theta}\left( x \right)=\theta_0+\theta_1x ，或者记为向量的形式（令 x_0\equiv1 ） h\left( x \right)=\sum_{i=0}^{n}\theta_ix_i=\theta^{T}x 。

数据的维度 n 又称为特征（features）的个数，这里 n=2 。

程序需要一个机制去评估 h 函数，一般这个函数称为损失函数（loss function），描述 h 函数不好的程度，在这里使用均方差（ x\left( i \right) 的估计值与真实值 y\left( i \right) 差的平方和）作为损失函数： J\left( \theta \right)=\frac{1}{2m}\sum_{i=1}^{m}\left( h_{\theta}\left( x^{\left( i \right)} \right)-y^{\left( i \right)} \right)^2 。

由梯度下降法：

\theta_j:=\theta_j-\alpha\frac{\partial}{\partial \theta_j}J\left( \theta \right)

令 z=\left( h_{\theta}\left( x^{\left( i \right)} \right)-y^{\left( i \right)} \right)^2 ， u=h_{\theta}\left( x^{\left( i \right)} \right)-y^{\left( i \right)} ，那么 z=u^2 。

\begin{align*} \frac{\partial}{\partial \theta_j}J\left( \theta \right) &=\frac{\partial}{\partial \theta_j}\frac{1}{2m}\sum_{i=1}^{m}\left( h_{\theta}\left( x^{\left( i \right)} \right)-y^{\left( i \right)} \right)^2\\ &=\frac{1}{2m}\sum_{i=1}^{m}\frac{\partial z}{\partial u}\frac{\partial u}{\partial \theta_j}\\ &=\frac{1}{2m}\ast2\sum_{i=1}^{m}u\ast\frac{\partial u}{\partial \theta_j}\\ &=\frac{1}{m}\sum_{i=1}^{m}u\ast\frac{\partial u}{\partial \theta_j} \end{align*}

\begin{align*} \frac{\partial}{\partial \theta_0}J\left( \theta \right) &=\frac{1}{m}\sum_{i=1}^{m}u\ast\frac{\partial u}{\partial \theta_0}\\ &=\frac{1}{m}\sum_{i=1}^{m}\left( h_{\theta}\left( x^{\left( i \right)} \right)-y^{\left( i \right)} \right)\ast\frac{\partial }{\partial \theta_0}\left( h_{\theta}\left( x^{\left( i \right)} \right)-y^{\left( i \right)} \right)\\ &=\frac{1}{m}\sum_{i=1}^{m}\left( \theta_0+\theta_1x^{\left( i \right)}-y^{\left( i \right)} \right)\ast\frac{\partial }{\partial \theta_0}\left( \theta_0+\theta_1x^{\left( i \right)}-y^{\left( i \right)} \right)\\ &=\frac{1}{m}\sum_{i=1}^{m}\left( \theta_0+\theta_1x^{\left( i \right)}-y^{\left( i \right)} \right)\\ &=\frac{1}{m}\sum_{i=1}^{m}\left( h_{\theta}\left( x^{\left( i \right)} \right)-y^{\left( i \right)} \right) \end{align*}

\begin{align*} \frac{\partial}{\partial \theta_1}J\left( \theta \right) &=\frac{1}{m}\sum_{i=1}^{m}u\ast\frac{\partial u}{\partial \theta_1}\\ &=\frac{1}{m}\sum_{i=1}^{m}\left( h_{\theta}\left( x^{\left( i \right)} \right)-y^{\left( i \right)} \right)\ast\frac{\partial }{\partial \theta_1}\left( h_{\theta}\left( x^{\left( i \right)} \right)-y^{\left( i \right)} \right)\\ &=\frac{1}{m}\sum_{i=1}^{m}\left( \theta_0+\theta_1x^{\left( i \right)}-y^{\left( i \right)} \right)\ast\frac{\partial }{\partial \theta_1}\left( \theta_0+\theta_1x^{\left( i \right)}-y^{\left( i \right)} \right)\\ &=\frac{1}{m}\sum_{i=1}^{m}\left( \theta_0+\theta_1x^{\left( i \right)}-y^{\left( i \right)} \right)\ast x^{\left( i \right)}\\ &=\frac{1}{m}\sum_{i=1}^{m}\left( h_{\theta}\left( x^{\left( i \right)} \right)-y^{\left( i \right)} \right)\ast x^{\left( i \right)} \end{align*}

\theta_0:=\theta_0-\alpha\ast\frac{\partial}{\partial \theta_0}J\left( \theta \right)=\theta_0-\alpha\ast\frac{1}{m}\sum_{i=1}^{m}\left( h_{\theta}\left( x^{\left( i \right)} \right)-y^{\left( i \right)} \right)

\theta_1:=\theta_1-\alpha\ast\frac{\partial}{\partial \theta_1}J\left( \theta \right)=\theta_1-\alpha\ast\frac{1}{m}\sum_{i=1}^{m}\left( h_{\theta}\left( x^{\left( i \right)} \right)-y^{\left( i \right)} \right)\ast x^{\left( i \right)}

（注：假如是多维输入，那么 \theta_j:=\theta_j-\alpha\ast\frac{\partial}{\partial \theta_j}J\left( \theta \right)=\theta_j-\alpha\ast\frac{1}{m}\sum_{i=1}^{m}\left( h_{\theta}\left( x^{\left( i \right)} \right)-y^{\left( i \right)} \right)\ast x_j^{\left( i \right)} ）

clear all;clc;
x_train = [2.5, 3.5, 6.3, 9.9, 9.91, 8.02, 4.5, 5.5, 6.23, 7.923,...
              2.941, 5.02, 6.34, 7.543, 7.546, 8.744, 9.674, 9.643, 5.33, 5.31,...
              6.78, 1.01, 9.68, 9.99, 3.54, 6.89, 10.9];
y_train = [3.34, 3.86, 5.63, 7.78, 10.6453, 8.43, 4.75, 5.345, 6.546, 7.5754,...
              2.35654, 5.43646, 6.6443, 7.64534, 7.546, 8.7457, 9.6464, 9.74643, 6.32, 6.42,...
              6.1243, 1.088, 10.342, 9.24, 4.22, 5.44, 9.33];
plot(x_train,y_train,'b*','Linewidth',2);hold on;
theta_0 =1; theta_1 =1; alpha = 0.01; J=10; m=length(x_train);
while(J>0.26)
    sum0=0;sum1=0;sum2=0;
    for i=1:m
        sum0=sum0+theta_0+theta_1*x_train(i)-y_train(i);
        sum1=sum1+(theta_0+theta_1*x_train(i)-y_train(i))*x_train(i);
        sum2=sum2+(theta_0+theta_1*x_train(i)-y_train(i))^2;
    end
    J=(1/(2*m))*sum2;
    theta_0=theta_0-alpha*(1/m)*sum0;
    theta_1=theta_1-alpha*(1/m)*sum1;
end
x=[1:0.1:11];
y=theta_0+theta_1*x;
plot(x,y,'r-','Linewidth',2);
print -djpeg -r600 example3

吴恩达的机器学习讲义中还给出了求解线性回归的最小二乘法： \theta=\left( X^TX \right)^{-1}X^T{\vec y} 。公式证明请参考【4】4.4，其他相关资料可参考【5】、【6】、【7】。

3.1 梯度下降法变体1——批量梯度下降法（Batch gradient descent，BGD）

批量梯度下降法是梯度下降法最原始的形式，它的具体思路是在更新每一参数时都使用所有的样本来进行更新，其数学形式为： \theta_j^{'}=\theta_j-\alpha\ast\frac{1}{m}\sum_{i=1}^{m}\left( h_{\theta}\left( x^{\left( i \right)} \right)-y^{\left( i \right)} \right)\ast x_j^{\left( i \right)} 。（推导过程请参见2.1.3）

repeat{
\theta_j^{'}=\theta_j-\alpha\ast\frac{1}{m}\sum_{i=1}^{m}\left( h_{\theta}\left( x^{\left( i \right)} \right)-y^{\left( i \right)} \right)\ast x_j^{\left( i \right)}
(for every j=0,...,n)
}

clear all;clc;
%y_train=theta_0*x_train_0+theta_1*x_train_1+theta_2*x_train_2
x_train_0 = [1,   1,   1,   1,   1,   1,   1,   1,   1,   1];
x_train_1 = [1.1, 1.3, 1.5, 1.7, 1.9, 2.1, 2.3, 2.5, 2.7, 2.9];
x_train_2 = [1.5, 1.9, 2.3, 2.7, 3.1, 3.5, 3.9, 4.3, 4.7, 5.1];
y_train =   [2.5; 3.2; 3.9; 4.6; 5.3; 6.0; 6.7; 7.4; 8.1; 8.8];
theta_0 =1; theta_1 =1; theta_2=1;
alpha = 0.1; m=length(x_train_0); eposize=5000; J=(eposize);
for i=1:eposize
    sum=0;sum_0=0;sum_1=0;sum_2=0;
    for j=1:m
        sum=sum+(theta_0*x_train_0(j)+theta_1*x_train_1(j)+theta_2*x_train_2(j)-y_train(j))^2;
        sum_0=sum_0+(theta_0*x_train_0(j)+theta_1*x_train_1(j)+theta_2*x_train_2(j)-y_train(j))*x_train_0(j);
        sum_1=sum_1+(theta_0*x_train_0(j)+theta_1*x_train_1(j)+theta_2*x_train_2(j)-y_train(j))*x_train_1(j);
        sum_2=sum_2+(theta_0*x_train_0(j)+theta_1*x_train_1(j)+theta_2*x_train_2(j)-y_train(j))*x_train_2(j);
    end
    theta_0=theta_0-alpha*(1/m)*sum_0;
    theta_1=theta_1-alpha*(1/m)*sum_1;
    theta_2=theta_2-alpha*(1/m)*sum_2;
    J(i)=(1/(2*m))*sum;
end
x_predict_0=[1, 1, 1, 1, 1];
x_predict_1=[3.1, 3.3, 3.5, 3.7, 3.9];
x_predict_2=[5.5, 5.9, 6.3, 6.7, 7.1];
for k=1:length(x_predict_0)
    y_predict(k) = theta_0*x_predict_0(k)+theta_1*x_predict_1(k)+theta_2*x_predict_2(k);
end
plot([1:1:eposize],J,'r-','Linewidth',0.5);
print -djpeg -r600 BGD

结果：

y_predict =
    9.5000   10.2000   10.9000   11.6000   12.3000

3.2 梯度下降法变体2——随机梯度下降法（Stochastic Gradient Descent，SGD）

由于批梯度下降每更新一个参数的时候，要用到所有的样本数，所以训练速度会随着样本数量的增加而变得非常缓慢。随机梯度下降正是为了解决这个办法而提出的。它是利用每个样本的损失函数对 \theta 求偏导得到对应的梯度，来更新 \theta ： \theta^{'}_j=\theta_j-\alpha\left( h_\theta\left( x^\left( i \right) \right)-y^\left( i \right) \right)x_j^\left( i \right) 。

1. Randomly shuffle dataset;
2. repeat{
for i=1,...,m{
\theta^{'}_j=\theta_j-\alpha\left( h_\theta\left( x^\left( i \right) \right)-y^\left( i \right) \right)x_j^\left( i \right)
(for j=0,...,n)
}
}

clear all;clc;
%为了方便大家清楚认识，这里不用矩阵的形式
%y_train=theta_0*x_train_0+theta_1*x_train_1+theta_2*x_train_2
x_train_0 = [1,   1,   1,   1,   1,   1,   1,   1,   1,   1];
x_train_1 = [1.1, 1.3, 1.5, 1.7, 1.9, 2.1, 2.3, 2.5, 2.7, 2.9];
x_train_2 = [1.5, 1.9, 2.3, 2.7, 3.1, 3.5, 3.9, 4.3, 4.7, 5.1];
y_train =   [2.5; 3.2; 3.9; 4.6; 5.3; 6.0; 6.7; 7.4; 8.1; 8.8];
theta_0 =1; theta_1 =1; theta_2=1;
alpha = 0.1; m=length(x_train_0); eposize=5000; J=(eposize);
rand_num=1;
for i=1:eposize
    %抽取rand_num对应的样本进行更新
    theta_0=theta_0-alpha*(theta_0*x_train_0(rand_num)+theta_1*x_train_1(rand_num)+theta_2*x_train_2(rand_num)-y_train(rand_num))*x_train_0(rand_num);
    theta_1=theta_1-alpha*(theta_0*x_train_0(rand_num)+theta_1*x_train_1(rand_num)+theta_2*x_train_2(rand_num)-y_train(rand_num))*x_train_1(rand_num);
    theta_2=theta_2-alpha*(theta_0*x_train_0(rand_num)+theta_1*x_train_1(rand_num)+theta_2*x_train_2(rand_num)-y_train(rand_num))*x_train_2(rand_num);
    if rand_num == m
        rand_num=1;
    else
        rand_num=rand_num+1;
    end
    sum=0;
    for j=1:m
        sum=sum+(theta_0*x_train_0(j)+theta_1*x_train_1(j)+theta_2*x_train_2(j)-y_train(j))^2;
    end
    J(i)=(1/(2*m))*sum;
end
x_predict_0=[1, 1, 1, 1, 1];
x_predict_1=[3.1, 3.3, 3.5, 3.7, 3.9];
x_predict_2=[5.5, 5.9, 6.3, 6.7, 7.1];
for k=1:length(x_predict_0)
    y_predict(k) = theta_0*x_predict_0(k)+theta_1*x_predict_1(k)+theta_2*x_predict_2(k);
end
plot([1:1:eposize],J,'r-','Linewidth',0.5);
print -djpeg -r600 SGD

结果：

y_predict =
    9.5000   10.2000   10.8999   11.5999   12.2999

随机梯度下降是通过每个样本来迭代更新一次，对比上面的批量梯度下降，迭代一次需要用到所有训练样本（往往如今真实问题训练数据都是非常巨大），一次迭代不可能最优，如果迭代10次的话就需要遍历训练样本10次。但是，SGD伴随的一个问题是噪音较BGD要多，使得SGD并不是每次迭代都向着整体最优化方向。

3.3 梯度下降法变体3——小批量梯度下降法（Mini-batch Gradient Descent，MBGD）

每次更新参数时使用b个样本（假设b为10），其具体的伪代码形式为：

Say b=10, m=1000.
Repeat{
for i=1, 11, 21, 31, ... , 991{
\theta_j:=\theta_j-\alpha\ast\frac{1}{10}\sum_{k=i}^{i+9}\left( h_{\theta}\left( x^{\left( k \right)} \right)-y^{\left( k \right)} \right)\ast x_j^{\left( k \right)}
(for every j=0, ... , n)
}
}

clear all; clc;
%y_train=theta_0*x_train_0+theta_1*x_train_1+theta_2*x_train_2
x_train_0 = [1,   1,   1,   1,   1,   1,   1,   1,   1,   1];
x_train_1 = [1.1, 1.3, 1.5, 1.7, 1.9, 2.1, 2.3, 2.5, 2.7, 2.9];
x_train_2 = [1.5, 1.9, 2.3, 2.7, 3.1, 3.5, 3.9, 4.3, 4.7, 5.1];
y_train =   [2.5; 3.2; 3.9; 4.6; 5.3; 6.0; 6.7; 7.4; 8.1; 8.8];
theta_0 =1; theta_1 =1; theta_2=1;
alpha = 0.1; m=length(x_train_0); eposize=5000; J=(eposize); a=1;
mini_batch_num=5;
for i=1:eposize
    %抽取mini_batch对应的样本进行更新
    sum_0=0;sum_1=0;sum_2=0;
    for ii=a:mini_batch_num
        sum_0 = sum_0+(theta_0*x_train_0(ii)+theta_1*x_train_1(ii)+theta_2*x_train_2(ii)-y_train(ii))*x_train_0(ii);
        sum_1 = sum_1+(theta_0*x_train_0(ii)+theta_1*x_train_1(ii)+theta_2*x_train_2(ii)-y_train(ii))*x_train_1(ii);
        sum_2 = sum_2+(theta_0*x_train_0(ii)+theta_1*x_train_1(ii)+theta_2*x_train_2(ii)-y_train(ii))*x_train_2(ii);
    end
    theta_0 = theta_0-alpha*(1/mini_batch_num)*sum_0;
    theta_1 = theta_1-alpha*(1/mini_batch_num)*sum_1;
    theta_2 = theta_2-alpha*(1/mini_batch_num)*sum_2;
    if a + mini_batch_num > m
        a = 1;
    else
        a = a + mini_batch_num;
    end
    sum=0;
    for j=1:m
        sum=sum+(theta_0*x_train_0(j)+theta_1*x_train_1(j)+theta_2*x_train_2(j)-y_train(j))^2;
    end
    J(i)=(1/(2*m))*sum;
end
x_predict_0=[1, 1, 1, 1, 1];
x_predict_1=[3.1, 3.3, 3.5, 3.7, 3.9];
x_predict_2=[5.5, 5.9, 6.3, 6.7, 7.1];
for k=1:length(x_predict_0)
    y_predict(k) = theta_0*x_predict_0(k)+theta_1*x_predict_1(k)+theta_2*x_predict_2(k);
end
plot([1:1:eposize],J,'r-','Linewidth',2);
print -djpeg -r600 MBGD

结果：

y_predict =
    9.5000   10.2000   10.9000   11.6000   12.3000

小结

1. BGD每次更新使用了所有的训练数据去最小化损失函数，缺点是如果样本值很大的话，更新速度会很慢。
2. SGD在每次更新的时候，只考虑了一个样本点，这样会加快训练过程，不过有可能由于训练数据的噪声点较多，那么每一次利用噪声点进行更新的过程中，就不一定是朝着极小值方向更新，但是由于更新多轮，整体方向还是大致朝着极小值方向更新，又提高了速度。
3. MBGD是为了解决BGD的训练速度慢，以及SGD的准确性综合而来。

4.1 指数加权移动平均（Exponential Weighted Moving Average）

• 4.1.1 加权平均VS算术平均

算术平均数

一般地，对于 n 个数 x_{1},x_{2},x_{3},...,x_{n} 我们把 \frac{1}{n}(x_{1}+x_{2}+x_{3}+...+x_{n}) 叫做这 n 个数的算术平均数，记作 \bar{x} 。

加权平均数

在实际问题中，一组数据里的各个数据的重要程度未必相同。加权平均数一般来说，如果在 n 个数中， x_{1} 出现的 f_{1} 次， x_{2} 出现 f_{2} 次，...， x_{k} 出现 f_{k} 次 (f_{1}+f_{2}+f_{3}+...+f_{k}=n) ，则 \bar{x}=\frac{1}{n}(x_{1}f_{1}+x_{2}f_{2}+x_{3}f_{3}+x_{k}f_{k}) ，其中 f_{1},f_{2},f_{3}...f_{k} 叫做权。

算术平均数与加权平均数的区别

算术平均数是加权平均数的一种特殊情况（各项的权相等为1)；在实际问题中，各项权不相等的时，计算平均数时就要采用加权平均数，当各项权相等时，计算平均数就要采用算术平均数。

加权平均数中的权的形式

整数的形式
比的形式
百分比的形式

• 4.1.2 指数加权移动平均

下图是一个关于天数和温度的散点图：

我们现在直接给出公式： v_{t}=\beta*v_{t-1}+(1-\beta)\theta_{t} 。

其中 v_{t} 代表到第 t 天的平均温度值， \theta_{t} 代表第 t 天的实际温度值 ， \beta 代表示加权下降的快慢，值越小权重下降的越快。

v_{t}\approx\frac{1}{(1-\beta)}\textrm{ day's temperature} （后面会说明原因）
当 \beta =0.9 时，指数加权平均最后的结果如图中红色线所示（ v_{t}\approx10\textrm{ day's temperature} 相当于粗略平均了过去10天的温度）；
当 \beta =0.98 时，指数加权平均最后的结果如图中绿色线所示（ v_{t}\approx50\textrm{ day's temperature} 相当于粗略平均了过去50天的温度，得到的曲线更平坦，波动更小，这是因为多平均了几天的温度，缺点是曲线进一步右移，因为指数加权平均公式中 \beta =0.98 ，相当于给前一天的值增加了太多权重，只有 0.02 的权重给了当日的值，在温度变化时，适应地更缓慢一些，所以会出现一定的延迟）；
当 \beta =0.5 时，指数加权平均最后的结果如下图中黄色线所示（ v_{t}\approx2\textrm{ day's temperature} 相当于粗略平均了过去2天的温度，平均的数据太少，得到的曲线有更多的噪声，也更有可能出现异常值，但是这个曲线能够更快适应温度的变化）。

当 \beta =0.9 时：

\begin{align*} v_{100} &= 0.9v_{99}+0.1\theta_{100}\\ v_{99} &= 0.9v_{98}+0.1\theta_{99}\\ v_{98} &= 0.9v_{97}+0.1\theta_{98}\\ \ldots \end{align*}

展开，有：

\begin{align*} v_{100} &=0.1\theta_{100}+0.9(0.1\theta_{99}+0.9(0.1\theta_{98}+0.9v_{97}))\\ &=0.1\theta_{100}+0.1\times0.9\theta_{99}+0.1\times(0.9)^{2}\theta_{98}+0.1\times(0.9)^{3}\theta_{97}+0.1\times(0.9)^{4}\theta_{96}\cdots \end{align*}

（注：上式中所有 \theta 前面的系数相加起来为 1 或者接近于 1 ，称之为偏差修正。）

分析 v_{100} 组成，即在一年第100天计算的数据，包括 \theta_{100} 、 \theta_{99} 、 \theta_{98} 、 \theta_{97} 、 \theta_{96} 等等。

从公式中可以看到：每天温度 \theta_t 的权重系数以指数等比形式缩小，时间越靠近当前时刻的数据加权影响力越大。

到底需要平均多少天的温度？

存在 (1-\varepsilon)^{1/\varepsilon}=\dfrac{1}{e} ，在上例中， 1-\varepsilon=\beta=0.9 ， \varepsilon=0.1 ，即 0.9^{10}\approx 0.35\approx\dfrac{1}{e} 。相当于大约10天后，权重下降到原来的 \dfrac{1}{e} 。仿佛我们在计算一个指数加权平均数，只关注了过去10天的天气，因为10天后，权重下降到不到当日权重的三分之一（假如 \beta=0.98 ，那么 (1-0.02)^{1/0.02=50}=\dfrac{1}{e} ，则过去了50天，权重才会下降当日权重的三分之一）。则得到结论： v_{t}\approx\frac{1}{(1-\beta)}\textrm{ day's temperature} 。

• 4.1.3 指数加权平均实现

\begin{align*} v_{0}&=0\\ v_{1}&=\beta v_{0}+(1-\beta)\theta_{1}\\ v_{2}&=\beta v_{1}+(1-\beta)\theta_{2}\\ v_{3}&=\beta v_{2}+(1-\beta)\theta_{3}\\ \ldots \end{align*}

因为，在计算当前时刻的平均值，只需要前一天的平均值和当前时刻的值，所以在数据量非常大的情况下，指数加权平均在节约计算成本的方面是一种非常有效的方式，可以很大程度上减少计算机资源存储和内存的占用。

• 4.1.4 指数加权平均的偏差修正

在我们执行指数加权平均的公式时，当 \beta=0.98 时，我们得到的并不是图中的绿色曲线，而是下图中的紫色曲线，其起点比较低。通过紫色曲线我们看出在预测的初期值和我的真实值的差距很大，所以引入了偏差修正的概念。

原因：

\begin{align*} v_{0}&=0\\ v_{1}&=0.98v_{0}+0.02\theta_{1}=0.02\theta_{1}\\ v_{2}&=0.98v_{1}+0.02\theta_{2}=0.98\times0.02\theta_{1}+0.02\theta_{2}=0.0196\theta_{1}+0.02\theta_{2} \end{align*}

如果第一天的值为如 40 ，则 v_{1}=0.02\times40=8 ，得到的值要远小于实际值，后面几天的情况也会由于初值引起的影响，均低于实际均值。

偏差修正：

指数加权平均公式 v_{t}=\beta v_{t-1}+(1-\beta)\theta_{t}

带修正偏差的指数加权平均公式 v_{t}^{'}=\frac{v_{t}}{1-\beta^{t}}=\frac{(\beta v_{t-1}+(1-\beta)\theta_t)}{1-\beta^{t}}

使用 v_{1}=0.02\times40=8 ，当 t=2 时：

1-\beta^{t}=1-(0.98)^{2}=0.0396

v_2^{'}= \dfrac{v_{2}}{0.0396}=\dfrac{0.0196\theta_{1}+0.02\theta_{2}}{0.0396}

偏差修正得到了绿色的曲线，在开始的时候，能够得到比紫色曲线更好的计算平均的效果。

对于 1-\beta^{t} 我们可以看出，随着 t 的逐渐增大， \beta^{t} 会逐渐接近与0，那么 1-\beta^{t} 就会逐渐接近与1，那么我们从公式上可以看出，我们的偏差修正最终会变成（如果数据多的话） v^{'}_{t}=v_{t} ，公式最终会变成 v^{'}_{t}=v_{t}=\beta v_{t-1}+(1-\beta)\theta_{t} 。所以在机器学习中，在计算指数加权平均数的大部分时候，大家不太在乎偏差修正，大部分宁愿熬过初始阶段，拿到具有偏差的估测，然后继续计算下去。如果你关心初始时期的偏差，修正偏差能帮助你在早期获得更好的估测。

5.1 梯度下降优化算法1——动量梯度下降法

SGD很难在陡谷中找到正确更新方向。而这种陡谷，经常在局部极值中出现。在这种情况下，如下图左所示，SGD在陡谷的周围震荡，向局部极值处缓慢地前进。

动量法，如上图右所示，则帮助SGD在相关方向加速前进，并减少它的震荡。对于动量梯度下降算法，其更新方程如下：

v_t =\gamma v_{t-1}+\alpha\nabla J(\theta)

\theta =\theta -v_t

（注：超参 \gamma ，一般取接近 1 的值如 0.9 ）

可以看到，参数更新时不仅考虑当前梯度值，而且加上了一个积累项（动量）。从本质上说，动量法，就仿佛我们从高坡上推下一个球，小球在向下滚动的过程中积累了动量，在途中它变得越来越快（直到它达到了峰值速度，如果有空气阻力的话， \gamma<1 ）。在我们的算法中，相同的事情发生在我们的参数更新上：动量项在梯度指向方向相同的方向逐渐增大，对梯度指向改变的方向逐渐减小。由此，我们得到了更快的收敛速度以及减弱的震荡。

• 5.1.1 算法实践

On integration t :
Compute dW , db on the current mini-batch
v_{dW}=\beta v_{dW}+\left( 1-\beta \right)dW
v_{db}=\beta v_{db}+\left( 1-\beta \right)db
W=W-\alpha v_{dW}
b=b-\alpha v_{db}

那么你有两个超参数， \alpha 和 \beta （ \beta 最常用的值是0.9，之前用来平均十天的温度，这次将平均前十次迭代的梯度），（查阅一些文献发现）很多时候将 1-\beta 去掉，那么得到：

v_{dW}=\beta v_{dW}+dW
v_{db}=\beta v_{db}+db

此时 \alpha 要根据 \frac{1}{1-\beta} 相应的变化（吴恩达老师建议用前者更直观）。

• 5.1.2 TensorFlow中提供了动量梯度下降算法的实现

tf.train.MomentumOptimizer(learning_rate=learning_rate, momentum=0.9)

（PS：Matlab for Mac用起来特别卡，还是pycharm比较流畅，之后的代码将用python完成。）

• 5.1.3 示例

考虑一个一元函数 \mathrm{func}\left( x \right) ，它的一阶导数为 \mathrm{d}x 。

普通梯度下降法 x=x-v ，每次 x 更新量 v 为 v=\alpha \cdot \mathrm{d}x 。

动量梯度下降法中每次 x 更新量 v 为 v=\alpha\cdot \mathrm{d}x+\beta\cdot v 。

import numpy as np
import matplotlib.pyplot as plt
import os
import shutil

# 用文件夹Images来存放每次plot的pic
folderName = 'Images'
if os.path.exists(folderName):
	shutil.rmtree(folderName)
os.mkdir(folderName)

# 目标函数:y=x^2
def func(x):
	return np.square(x)


# 目标函数一阶导数:dy/dx=2*x
def dfunc(x):
	return 2 * x


def GD_momentum(x_start, df, epochs, alpha, beta):
    """
    动量梯度下降法
    input:
    x_start   x的起始点
    df        目标函数的一阶导函数
    epochs    迭代周期
    alpha     学习率
    beta      冲量

    return:
    x在每次迭代后的位置（包括起始点），长度为epochs+1
    """
    xs = np.zeros(epochs+1)
    x = x_start
    xs[0] = x
    v = 0
    for i in range(epochs):
        dx = df(x)
	v = alpha * dx + beta * v
	x = x - v
	xs[i+1] = x
    return xs


line_x = np.linspace(-5, 5, 100)
line_y = func(line_x)
x_start = -5
epochs = 6
alpha = [0.01, 0.1, 0.6, 0.9]
beta = [0.0, 0.1, 0.5, 0.9]
color = ['k', 'r', 'g', 'y']
size = np.ones(epochs+1) * 10  # size的长度为epochs+1
size[-1] = 70  # 将size中倒数第一个元素置为70
for i in range(len(alpha)):
	for j in range(len(beta)):
		plt.figure(figsize=(10, 10))  # 创建画图的窗口
		x = GD_momentum(x_start, dfunc, epochs, alpha=alpha[i], beta=beta[j])
		plt.title(r'$\alpha$=' + str(alpha[i]) + r'$\beta$=' + str(beta[j]), fontsize=30)
		plt.plot(line_x, line_y, c='b', linewidth=2.5)  # 画出y=x^2的曲线
		plt.plot(x, func(x), c=color[i], linewidth=2.5)
		plt.scatter(x, func(x), c=color[i], s=size)
		plt.xticks(fontsize=15)
		plt.yticks(fontsize=15)
		plt.savefig(os.path.join(folderName, "alpha" + str(alpha[i]) + "_" + "beta" + str(beta[j])) + ".png")

结果：

从第一张图可看出：在学习率较小的时候，适当的 \beta 能够起到一个加速收敛速度的作用。
从第四张图可看出：在学习率较大的时候，适当的 \beta 能够起到一个减小收敛时震荡幅度的作用。

6.1 Nesterov加速梯度法

当一个小球从山谷上滚下的时候，盲目的沿着斜率方向前行，其效果并不令人满意。我们需要有一个更“聪明”的小球，它能够知道它再往哪里前行，并在知道斜率再度上升的时候减速。

Nesterov加速梯度法（Nesterov accelerated gradient，NAG）是一种能给予梯度项上述“预测”功能的方法。我们知道，我们使用动量项 \gamma v_{t-1} 来“移动”参数项 \theta 。通过计算 \theta-\gamma v_{t-1} ，我们能够得到一个下次参数位置的近似值——也就是能告诉我们参数大致会变为多少。那么，通过基于未来参数的近似值而非当前的参数值计算相得应罚函数 J\left( \theta -\gamma v_{t-1} \right) 并求偏导数，我们能让优化器高效地“前进”并收敛：

v_t=\gamma v_{t-1}+\alpha\nabla_{\theta} J\left( \theta -\gamma v_{t-1} \right)

\theta =\theta - v_t

在该情况下，我们依然设定动量系数 \gamma 在0.9左右。

这种基于预测的更新方法，使我们避免过快地前进，并提高了算法地响应能力，大大改进了RNN在一些任务上的表现。

因为我们现在能根据我们罚函数的梯度值来调整我们的更新，并能相应地加速SGD，我们也希望能够对罚函数中的每个参数调整我们的更新值，基于它们的重要性以进行或大或小的更新。

• 6.1.1 TensorFlow中的NAG优化器

tf.train.MomentumOptimizer(learning_rate=learning_rate, momentum=0.9, use_nesterov=True)

• 6.1.2 示例

v_0=0

v_1=\alpha\nabla_{\theta} J\left( \theta -\gamma v_0 \right)

v_2=\alpha\nabla_{\theta} J\left( \theta -\gamma v_1 \right)

v_3=\alpha\nabla_{\theta} J\left( \theta -\gamma v_2 \right)

...

v_t=\gamma v_{t-1}+\alpha\nabla_{\theta} J\left( \theta -\gamma v_{t-1} \right)

\theta_\mathrm{new}=\theta-v_t

import numpy as np
import matplotlib.pyplot as plt
import os
import shutil

# 用文件夹Images来存放每次plot的pic
folderName = 'Images'
if os.path.exists(folderName):
	shutil.rmtree(folderName)
os.mkdir(folderName)

# 目标函数:y=x^2
def func(x):
	return np.square(x)


# 目标函数一阶导数:dy/dx=2*x
def dfunc(x):
	return 2 * x


def NAG(x_start, df, epochs, alpha, gamma):
    """
    NAG下降法
    input:
    x_start   x的起始点
    df         目标函数的一阶导函数
    epochs  迭代周期
    alpha     学习率
    beta      冲量

    return:
    x在每次迭代后的位置（包括起始点），长度为epochs+1
    """
	xs = np.zeros(epochs+1)
	x = x_start
	xs[0] = x
	v = 0
	for i in range(epochs):
		dx = df(x - gamma * v)
		v = alpha * dx + gamma * v
		x = x - v
		xs[i+1] = x
	return xs


line_x = np.linspace(-5, 5, 100)
line_y = func(line_x)
x_start = -5
epochs = 6
alpha = [0.01, 0.1, 0.6, 0.9]
gamma = [0.0, 0.1, 0.5, 0.9]
color = ['k', 'r', 'g', 'y']
size = np.ones(epochs+1) * 30  # size的长度为epochs+1
size[-1] = 100  # 将size中倒数第一个元素置为70
for i in range(len(alpha)):
	for j in range(len(gamma)):
		plt.figure(figsize=(10, 10))  # 创建画图的窗口
		x = NAG(x_start, dfunc, epochs, alpha=alpha[i], gamma=gamma[j])
		plt.title('NAG(' + r'$\alpha$=' + str(alpha[i]) + r'$\gamma$=' + str(gamma[j])+')', fontsize=30)
		plt.plot(line_x, line_y, c='b', linewidth=2.5)  # 画出y=x^2的曲线
		plt.plot(x, func(x), c=color[i], linewidth=2.5)
		plt.scatter(x, func(x), c=color[i], s=size)
		plt.xticks(fontsize=15)
		plt.yticks(fontsize=15)
		plt.savefig(os.path.join(folderName, "alpha" + str(alpha[i]) + "_" + "gamma" + str(gamma[j])) + ".png")

结果（左列为动量梯度下降法，右列为NAG加速梯度法）：

7.1 Adagrad法

Adagrad是一个基于梯度的优化算法，它的主要功能是：对不同的参数调整学习率，具体而言，对低频出现的参数进行大的更新，对高频出现的参数进行小的更新。因此，它很适合于处理稀疏数据。

在这之前，我们对于所有的参数 \theta 使用相同的学习率 \alpha 进行更新。但Adagrad则不然，对不同的训练迭代次数 t ，Adagrad对每个参数 \theta_i 都有一个不同的学习率。我们首先考察Adagrad每个参数的的更新过程，然后我们再使之向量化。为简洁起见，我们记在迭代次数 t 下，对参数 \theta_i 求目标函数梯度的结果为 g_{t,i} ：

g_{t,i}=\nabla_{\theta_t} J\left( \theta_{t,i} \right)

那么普通SGD的更新规则为：

\theta_{t+1,i}=\theta_{t,i}-\alpha \cdot g_{t,i}

而Adagrad将学习率 \alpha 进行了修正，对迭代次数 t ，基于每个参数 \theta_i 之前计算的梯度值，将每个参数 \theta_i 的学习率 \alpha 按如下方式修正：

\theta_{t+1,i}=\theta_{t,i}-\frac{\alpha}{\sqrt{G_{t,ii}+\epsilon}}\cdot g_{t,i}
其中 G_t \in {\Bbb R}^{d \times d} 是一个对角阵，其中对角线上的元素 G_{t,ii} 是从一开始到 t 时刻目标函数对于参数 \theta_i 梯度的平方和。 \epsilon 是一个平滑项，以避免分母为0的情况，它的数量级通常在 1e-8 。有趣的是，如果不开方的话，这个算法的表现会变得很糟。

因为 G_t 在其对角线上，含有过去目标函数对于参数 \theta_i 梯度的平方和，我们可以利用一个元素对元素的向量乘法 \odot ，将我们的表达式向量化：

\theta_{t+1,i}=\theta_{t,i}-\frac{\alpha}{\sqrt{G_{t,ii}+\epsilon}}\odot g_{t,i}

Adagrad的主要优势之一，是它不需要对每个学习率手工地调节。而大多数算法，只是简单地使用一个相同地默认值如0.1，来避免这样地情况。

Adagrad的主要劣势，是它在分母上的 G_t 项中积累了平方梯度和。因为每次加入的项总是一个正值，所以累积的和将会随着训练过程而增大。因而，这会导致学习率不断缩小，并最终变为一个无限小值——此时，这个算法已经不能从数据中学到额外的信息。

• 7.1.1 TensorFlow中的Adagrad优化器

tf.train.AdagradOptimizer.__init__(learning_rate, initial_accumulator_value=0.1, use_locking=False, name=’Adagrad’)

• 7.1.2 示例

import numpy as np
import matplotlib.pyplot as plt
import os
import shutil

# 用文件夹Adagrad Images来存放每次plot的pic
folderName = 'Adagrad Images'
if os.path.exists(folderName):
	shutil.rmtree(folderName)
os.mkdir(folderName)

# 目标函数:y=x^2
def func(x):
	return np.square(x)


# 目标函数一阶导数:dy/dx=2*x
def dfunc(x):
	return 2 * x


def Adagrad(x_start, df, epochs, alpha, epsilon):
    """
    Adagrad法
    input:
    x_start     x的起始点
    df           目标函数的一阶导函数
    epochs    迭代周期
    alpha      学习率
    epsilon    平滑项以避免分母为0的情况

    return:
    x在每次迭代后的位置（包括起始点），长度为epochs+1
    """
	xs = np.zeros(epochs+1)
	x = x_start
	xs[0] = x
	v = 0
	for i in range(epochs):
		v = v + np.square(df(x))
		x = x - (alpha / np.sqrt(v+epsilon)) * df(x)
		xs[i+1] = x
	return xs


line_x = np.linspace(-5, 5, 100)
line_y = func(line_x)
x_start = -5
epochs = 6
epsilon = 1e-8
alpha = [0.01, 0.05, 0.1, 0.5]
size = np.ones(epochs+1) * 30  # size的长度为epochs+1
size[-1] = 100  # 将size中倒数第一个元素置为70
for i in range(len(alpha)):
	plt.figure(figsize=(10, 10))  # 创建画图的窗口
	x = Adagrad(x_start, dfunc, epochs, alpha=alpha[i], epsilon=epsilon)
	plt.title('Adagrad(' + r'$\alpha$=' + str(alpha[i]) + ')', fontsize=30)
	plt.plot(line_x, line_y, c='b', linewidth=2.5)  # 画出y=x^2的曲线
	plt.plot(x, func(x), c='g', linewidth=2.5)
	plt.scatter(x, func(x), c='g', s=size)
	plt.xticks(fontsize=15)
	plt.yticks(fontsize=15)
	plt.savefig(os.path.join(folderName, "alpha" + str(alpha[i])) + ".png")

结果：

（PS：之前介绍的方法还推荐大家阅读资料和程序【20】【21】【22】【23】【24】【25】【26】）

8.1 Adadelta法

Adadelta法是Adagrad法的一个延伸，它旨在解决Adagrad法学习率不断单调下降的问题。相比计算之前所有梯度值的平方和，Adadelta法仅计算在一个大小为 \omega 的时间区间内梯度值的累积和。

但该方法并不会存储之前 \omega 个梯度的平方值，而是将梯度值累积值按如下的方式递归地定义：它被定义为关于过去梯度值的衰减均值（decade average），当前时间 t 的梯度均值 E\left[ g^2 \right]_t 是基于过去梯度均值 E\left[ g^2 \right]_{t-1} 和当前梯度值平方 g^2_t 的加权平均，其中 \gamma 是类似上述动量项的权值。

E\left[ g^2 \right]_t=\gamma E\left[ g^2 \right]_{t-1}+\left( 1-\gamma \right)g^2_t

与动量项的设定类似，我们设定 \gamma 为以 0.9 左右的值。为明确起见，我们将SGD更新规则写为关于参数更新向量 \Delta\theta_t 的形式：

\Delta\theta_t=-\alpha \cdot g_{t,i}

\theta_{t+1}=\theta_t+\Delta\theta_t

由此，我们刚刚在Adagrad法中推导的的参数更新规则的向量表示，变为如下形式：

\Delta \theta_t=-\frac{\alpha}{\sqrt{G_t+\epsilon}} \odot g_t

我们现在将其中的对角矩阵 G_t 用上述定义的基于过去梯度平方和的衰减均值 E\left[ g^2 \right]_t 替换：

\Delta \theta_t=-\frac{\alpha}{\sqrt{E\left[ g^2 \right]_t+\epsilon}} \odot g_t

因为分母表达式的形式与梯度值的方均根（root mean squared，RMS）形式类似，因而我们使用相应的简写来替换：

\Delta \theta_t=-\frac{\alpha}{\mathrm{RMS}\left[ g \right]_t} \odot g_t （即 {\mathrm{RMS}\left[ g \right]_t}={\sqrt{E\left[ g^2 \right]_t+\epsilon}} ）

在该更新中（SGD、Momentum、Adagrad也类似）单位并不一致，也就是说，更新值的量纲与参数值的假设量纲并不一致。为改进这个问题，Adadelta算法如下：

Require: Decay rate \gamma , Constant \epsilon
Require: Initial parameter x_1
Initialize accumulation variables E\left[ g^2 \right]_{0}=0 E\left[ \Delta \theta^2 \right]_{0}
for t=1:T do %% Loop over # of updates
Compute Gradient: g_t
Accumulate Gradient: E\left[ g^2 \right]_t=\gamma E\left[ g^2 \right]_{t-1}+\left( 1-\gamma \right)g^2_t
Compute Update: \Delta\theta_t=-\frac{{\mathrm{RMS}\left[ \Delta\theta \right]_{t-1}}}{{\mathrm{RMS}\left[ g \right]_t}}g_t
Accumulate Updates: E\left[ \Delta\theta^2 \right]_t=\gamma E\left[ \Delta\theta^2 \right]_{t-1}+\left( 1-\gamma \right)\Delta\theta^2_t
Apply Update: \theta_{t+1}=\theta_t+\Delta\theta_t
end for

借助Adadelta法，我们甚至不需要预设一个默认学习率，因为它已经从我们的更新规则中被删除了。

• 8.1.1 TensorFlow中的Adadelta优化器

tf.train.AdadeltaOptimizer.init(learning_rate=0.001, rho=0.95, epsilon=1e-08, use_locking=False, name=’Adadelta’)

• 8.1.2 示例

import numpy as np
import matplotlib.pyplot as plt
import os
import shutil

# 用文件夹Adadelta Images来存放每次plot的pic
folderName = 'Adadelta Images'
if os.path.exists(folderName):
	shutil.rmtree(folderName)
os.mkdir(folderName)

# 目标函数:y=x^2
def func(x):
	return np.square(x)


# 目标函数一阶导数:dy/dx=2*x
def dfunc(x):
	return 2 * x


def Adadelta(x_start, df, epochs, epsilon, gamma):
    """
    Adadelta法
    input:
    x_start     x的起始点
    df           目标函数的一阶导函数
    epochs    迭代周期
    gamma    动量项权值
    epsilon    平滑项以避免分母为0的情况

    return:
    x在每次迭代后的位置（包括起始点），长度为epochs+1
    """
	xs = np.zeros(epochs+1)
	x = x_start
	xs[0] = x
	E_g = 0  # Initialize accumulation variables
	E_delta_x = 0  # Initialize accumulation variables
	RMS_delta_x = np.sqrt(E_delta_x + epsilon)
	for i in range(epochs):
		g = df(x)  # Compute Gradient
		E_g = gamma * E_g + (1-gamma) * np.square(g)  # Accumulate Gradient
		RMS_g = np.sqrt(E_g+epsilon)
		delta_x = -((RMS_delta_x)/(RMS_g)) * g  # Compute Update
		E_delta_x = gamma * E_delta_x + (1-gamma) * np.square(delta_x)  # Accumulate Updates
		RMS_delta_x = np.sqrt(E_delta_x+epsilon)
		x = x + delta_x  # Apply Update
		xs[i+1] = x
	return xs

line_x = np.linspace(-5, 5, 100)
line_y = func(line_x)
x_start = -5
epochs = 6
epsilon = [1e-3, 1e-4, 1e-5, 1e-6, 1e-7, 1e-8]
gamma = [0.9, 0.95]  # 动量项权值
size = np.ones(epochs+1) * 30  # size的长度为epochs+1
size[-1] = 100  # 将size中倒数第一个元素置为100
for i in range(len(gamma)):
	for j in range(len(epsilon)):
		plt.figure(figsize=(10, 10))  # 创建画图的窗口
		x = Adadelta(x_start, dfunc, epochs, epsilon=epsilon[j], gamma=gamma[i])
		plt.title('Adadelta' + '(' + r'$\gamma$=' + str(gamma[i]) + r'$\epsilon$=' + str(epsilon[j]) + ')', fontsize=30)
		plt.plot(line_x, line_y, c='b', linewidth=2.5)  # 画出y=x^2的曲线
		plt.plot(x, func(x), c='g', linewidth=2.5)
		plt.scatter(x, func(x), c='g', s=size)
		plt.xticks(fontsize=15)
		plt.yticks(fontsize=15)
		plt.savefig(os.path.join(folderName, "gamma" + str(gamma[i]) + "epsilon" + str(epsilon[j])) + ".png")

结果：

9.1 RMSprop

RMSprop是由Geoff Hinton在他Coursera课程中提出的一种适应性学习率方法，至今仍未被公开发表。RMSprop法和Adadelta法几乎同时被发展出来。他们解决Adagrad激进的学习率缩减问题。实际上， RMSprop和我们推导出的Adadelta法第一个更规则相同：

E\left[ g^2 \right]_t=0.9 E\left[ g^2 \right]_{t-1}+0.1g^2_t

\theta_{t+1}=\theta_t-\frac{\alpha}{\sqrt{E\left[ g^2 \right]_t+\epsilon}}g_t

RMSprop也将学习率除以了一个指数衰减的衰减均值。

（注：Hinton建议设定 \gamma 为0.9，对 \alpha 而言，0.001是一个较好的默认值。）

• 9.1.1 TensorFlow中的RMSprop优化器

tf.train.RMSPropOptimizer(learning_rate=learning_rate, momentum=0.9, decay=0.9, epsilon=1e-10)

• 9.1.2 示例

import numpy as np
import matplotlib.pyplot as plt
import os
import shutil

# 用文件夹RMSprop Images来存放每次plot的pic
folderName = 'RMSprop Images'
if os.path.exists(folderName):
	shutil.rmtree(folderName)
os.mkdir(folderName)

# 目标函数:y=x^2
def func(x):
	return np.square(x)


# 目标函数一阶导数:dy/dx=2*x
def dfunc(x):
	return 2 * x


def RMSprop(x_start, df, epochs, epsilon, alpha, gamma):
    """
    RMSpro法
    input:
    x_start     x的起始点
    df           目标函数的一阶导函数
    epochs    迭代周期
    alpha      学习率
    gamma    动量项权值
    epsilon    平滑项以避免分母为0的情况

    return:
    x在每次迭代后的位置（包括起始点），长度为epochs+1
    """
	xs = np.zeros(epochs+1)
	x = x_start
	xs[0] = x
	E = 0
	for i in range(epochs):
		E = gamma * E + (1-gamma) * np.square(df(x))
		delta_x = (alpha/np.sqrt(E + epsilon)) * df(x)
		x = x - delta_x
		xs[i+1] = x
	return xs

line_x = np.linspace(-5, 5, 100)
line_y = func(line_x)
x_start = -5
epochs = 20
epsilon = 1e-8
alpha = [0.001, 0.005, 0.01]  # 学习率
gamma = [0.9, 0.91, 0.95, 0.98]  # 动量项权值
size = np.ones(epochs+1) * 30  # size的长度为epochs+1
size[-1] = 100  # 将size中倒数第一个元素置为100
for i in range(len(alpha)):
	for j in range(len(gamma)):
		plt.figure(figsize=(10, 10))  # 创建画图的窗口
		x = RMSprop(x_start, dfunc, epochs, epsilon=epsilon, alpha=alpha[i], gamma=gamma[j])
		plt.title('RMSprop' + '(' + r'$\alpha=$' + str(alpha[i]) + r'$\gamma$=' + str(gamma[j]) + ' epochs=' + str(epochs) + ')', fontsize=30)
		plt.plot(line_x, line_y, c='b', linewidth=2.5)  # 画出y=x^2的曲线
		plt.plot(x, func(x), c='g', linewidth=2.5)
		plt.scatter(x, func(x), c='g', s=size)
		plt.xticks(fontsize=15)
		plt.yticks(fontsize=15)
		plt.savefig(os.path.join(folderName, "alpha" + str(alpha[i]) + "gamma" + str(gamma[j])) + ".png")

结果：

10.1 适应性动量估计法（Adaptive Moment Estimation，Adam）

适应性动量估计法是另一种能对不同参数计算适应性学习率的方法。除了存储类似Adadelta法或RMSprop中指数衰减的过去梯度平方均值 v_t 外，Adam法也存储像动量法中的指数衰减的过去梯度值均值 m_t :

m_t=\beta_1m_{t-1}+\left( 1-\beta_1 \right)g_t

v_t=\beta_2v_{t-1}+\left( 1-\beta_2 \right)g^2_t

概率论中矩的含义是：如果一个随机变量 X 服从某个分布， X 的一阶矩是 E(X) ，也就是样本平均值， X 的二阶矩就是 E(X^2)，也就是样本平方的平均值。

m_t 和 v_t 分别是梯度的一阶矩（均值）和二阶矩（表示不确定度的方差），这也就是该方法名字的来源。因为当 m_t 和 v_t 一开始被初始化为0向量时，Adam的作者观察到，该方法会有趋向0的偏差，尤其是在最初的几步或是在衰减率很小（即 \beta_1 和 \beta_2 接近1）的情况下。

他们使用偏差纠正系数，来修正一阶矩和二阶矩的偏差：

\hat m_t=\frac{m_t}{1-\beta_1^t}

\hat v_t=\frac{v_t}{1-\beta_2^t}

他们使用这些来更新参数，更新规则很我们在Adadelta和RMSprop法中看到的一样，服从Adam的更新规则：

\theta_{t+1}=\theta_t-\frac{\alpha}{\sqrt{\hat v_t}+\epsilon}\hat m_t

Adam算法
Require: 学习率 \alpha （建议默认为： \alpha=0.001 ）
Require: 矩估计的指数衰减速率， \beta_1 和 \beta_2 在区间 \left[ 0,1 \right) 内。（建议默认为： \beta_1=0.9 \beta_2=0.999 ）
Require: 用于数值稳定的小常数 \epsilon （建议默认为： \epsilon=10^{-8} ）
Require: 初始参数 \theta
初始化一阶和二阶矩变量 m_t=0 v_t=0
初始化时间步 t=0
while{没有达到停止准则}
计算梯度： g_t
t \leftarrow t+1
更新有偏一阶矩估计： m_t=\beta_1m_{t-1}+\left( 1-\beta_1 \right)g_t
更新有偏二阶矩估计： v_t=\beta_2v_{t-1}+\left( 1-\beta_2 \right)g^2_t
修正一阶矩的偏差： \hat m_t=\frac{m_t}{1-\beta_1^t}
修正二阶矩的偏差： \hat v_t=\frac{v_t}{1-\beta_2^t}
　　计算更新： \Delta\theta=-\frac{\alpha\hat m_t}{\sqrt{\hat v_t}+\epsilon} （逐元素应用操作）
　　执行更新： \theta \leftarrow \theta+\Delta\theta
end while

• 10.1.1 TensorFlow中的Adam优化器

tf.train.AdamOptimizer(learning_rate=0.001, beta1=0.9, beta2=0.999, epsilon=1e-08)

• 10.1.2 示例

import numpy as np
import matplotlib.pyplot as plt
import os
import shutil

# 用文件夹Adam Images来存放每次plot的pic
folderName = 'Adam Images'
if os.path.exists(folderName):
	shutil.rmtree(folderName)
os.mkdir(folderName)

# 目标函数:y=x^2
def func(x):
	return np.square(x)


# 目标函数一阶导数:dy/dx=2*x
def dfunc(x):
	return 2 * x


def Adam(x_start, df, epochs, epsilon, alpha, beta1, beta2):
    """
    Adam法
    input:
    x_start    x的起始点
    df         目标函数的一阶导函数
    epochs     迭代周期
    epsilon    小常数避免分母为0的情况
    alpha      学习率
    beta1      一阶矩估计的指数衰减速率
    beta2      二阶矩估计的指数衰减速率

    return:
    x在每次迭代后的位置（包括起始点），长度为epochs+1
    """
	xs = np.zeros(epochs+1)
	x = x_start  # 初始参数
	xs[0] = x
	m_t = 0  # 初始化一阶矩变量
	v_t = 0  # 初始化二阶矩变量
	for i in range(epochs):
		g = df(x)  # Compute Gradient
		m_t = beta1 * m_t + (1-beta1) * g  # 更新有偏一阶矩估计
		v_t = beta2 * v_t + (1 - beta2) * np.square(g)  # 更新有偏二阶矩估计
		m_t_hat = m_t / (1 - beta1**(i+1))  # 修正一阶矩的偏差
		v_t_hat = v_t / (1 - beta2**(i+1))  # 修正二阶矩的偏差
		delta_x = -(alpha * m_t_hat) / (np.sqrt(v_t_hat)+epsilon)  # 计算更新
		x = x + delta_x  # 执行更新
		xs[i+1] = x
	return xs


line_x = np.linspace(-5, 5, 100)
line_y = func(line_x)
x_start = -5
epochs = 6
alpha = 0.1
beta1 = 0.9
beta2 = 0.99
epsilon = 1e-8
size = np.ones(epochs+1) * 30  # size的长度为epochs+1
size[-1] = 100  # 将size中倒数第一个元素置为70

plt.figure(figsize=(10, 10))  # 创建画图的窗口
x = Adam(x_start, dfunc, epochs, epsilon=epsilon, alpha=alpha, beta1=beta1, beta2=beta2)
plt.title('Adam' + '(' + r'$\alpha$=' + str(alpha) + r'$\beta_1$=' + str(beta1) + r'$\beta_2$=' + str(beta2) + ')', fontsize=30)
plt.plot(line_x, line_y, c='b', linewidth=2.5)  # 画出y=x^2的曲线
plt.plot(x, func(x), c='g', linewidth=2.5)
plt.scatter(x, func(x), c='g', s=size)
plt.xticks(fontsize=15)
plt.yticks(fontsize=15)
plt.savefig(os.path.join(folderName, "alpha" + str(alpha) + "beta_1" + str(beta1) + "beta_2" + str(beta2)) + ".png")

结果：

11.1 学习速率 \alpha

如果 \alpha 设置得非常大，那么训练可能不会收敛，就直接发散了；
如果 \alpha 设置的比较小，虽然可以收敛，但是训练时间可能无法接受；
如果 \alpha 设置的稍微高一些，训练速度会很快，但是当接近最优点会发生震荡，甚至无法稳定。

理想的学习速率是：刚开始设置较大，有很快的收敛速度，然后慢慢衰减，保证稳定到达最优点。所以，前面的很多算法都是学习速率自适应的。除此之外，还可以手动实现这样一个自适应过程，如实现学习速率指数式衰减：

\alpha(t)=\alpha _{0}\cdot\frac{1}{10}^{\frac{t}{r}}

在TensorFlow中，你可以这样实现：

initial_learning_rate = 0.1
decay_steps = 10000
decay_rate = 1/10
global_step = tf.Variable(0, trainable=False)

learning_rate = tf.train.exponential_decay(initial_learning_rate, global_step, decay_steps, decay_rate)
# decayed_learning_rate = learning_rate *decay_rate ^ (global_step / decay_steps)
optimizer = tf.train.MomentumOptimizer(learning_rate, momentum=0.9)
training_op = optimizer.minimize(loss, global_step=global_step)

12.1 如何选择合适的优化算法

如果你的输入数据较为稀疏（sparse），那么使用适应性学习率类型的算法会有助于你得到好的结果。此外，使用该方法的另一好处是，你在不调参、直接使用默认值的情况下，就能得到最好的结果。

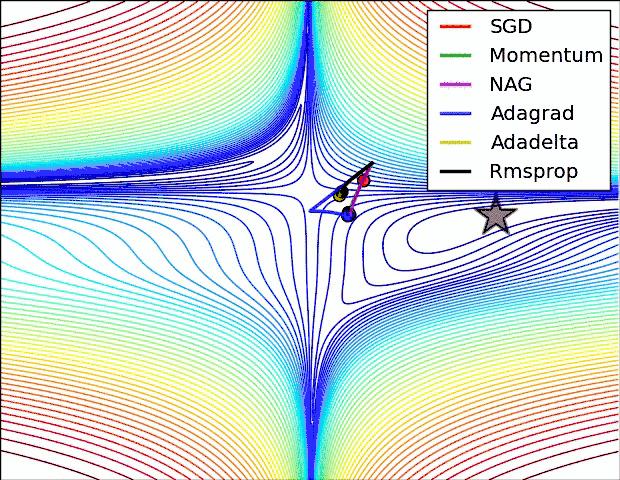
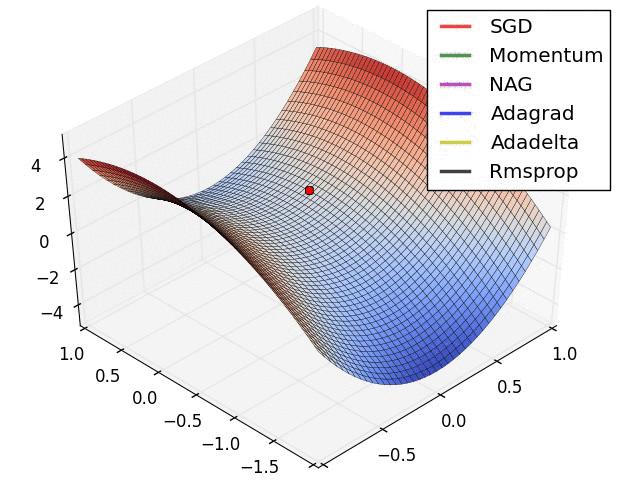
下面两幅图可以提供一些关于收敛速度的参考。

第一幅图展示了在代价函数误差等高线上几种不同的优化算法收敛速度情况；
第二幅图展示了在遇到鞍点时，算法的鲁棒性。

参考文献：

【1】深入浅出--梯度下降法及其实现

【2】Halfrost-Field——机器学习——梯度下降

【3】Halfrost-Field——机器学习——目录

【4】Linear Algebra Review and Reference

【5】斯坦福吴恩达机器学习课程主页

【6】梯度下降法的matlab实现

【7】cs229 斯坦福机器学习笔记（一）-- 入门与LR模型

【8】A vanilla machine learning library in Python

【9】[Machine Learning] 梯度下降法的三种形式BGD、SGD以及MBGD

【10】机器学习小组知识点4&5:批量梯度下降法(BGD)和随机梯度下降法(SGD)的代码实现Matlab版

【11】详解梯度下降法的三种形式BGD、SGD以及MBGD

【12】Goodfellow I, Bengio Y, Courville A, et al. Deep learning[M]. Cambridge: MIT press, 2016.

【13】吴恩达 改善深层神经网络：超参数调试、正则化以及优化 2.3 指数加权平均

【14】吴恩达 改善深层神经网络：超参数调试、正则化以及优化 2.4 理解指数加权平均

【15】吴恩达 改善深层神经网络：超参数调试、正则化以及优化 2.5 指数加权平均的偏差修正

【16】吴恩达 DeepLearning.ai 课程提炼笔记（2-2）改善深层神经网络 --- 优化算法

【17】通俗理解指数加权平均

【18】梯度下降法】二：冲量（momentum）的原理与Python实现

【19】吴恩达 改善深层神经网络：超参数调试、正则化以及优化 2.6 动量梯度下降法

【20】深度学习优化函数详解（0）-- 线性回归问题

【21】深度学习优化函数详解（1）-- Gradient Descent 梯度下降法

【22】深度学习优化函数详解（2）-- SGD 随机梯度下降

【23】深度学习优化函数详解（3）-- mini-batch SGD 小批量随机梯度下降

【24】深度学习优化函数详解（4）-- momentum 动量法

【25】深度学习优化函数详解（5）-- Nesterov accelerated gradient (NAG)

【26】深度学习优化函数详解（6）-- adagrad

【27】ADADELTA: AN ADAPTIVE LEARNING RATE METHOD

【28】深度学习中的常用训练算法

【29】深度学习最全优化方法总结比较（SGD，Adagrad，Adadelta，Adam，Adamax，Nadam）

【30】一文看懂常用的梯度下降算法

【31】An overview of gradient descent optimization algorithms

【32】吴恩达 改善深层神经网络：超参数调试、正则化以及优化 2.7 RMSprop

请大家批评指正，谢谢 ～