Hierarchical Softmax(层次Softmax)
在进行最优化的求解过程中:从隐藏层到输出的Softmax层的计算量很大,因为要计算所有词的Softmax概率,再去找概率最大的值。
除了上篇文章讲到的负采样可以解决,Hierarchical Softmax也可以解决该问题。
Huffman Tree(哈夫曼树)
哈夫曼树是一种带权路径长度最短的二叉树,也称为最优二叉树。下面用一幅图来说明:
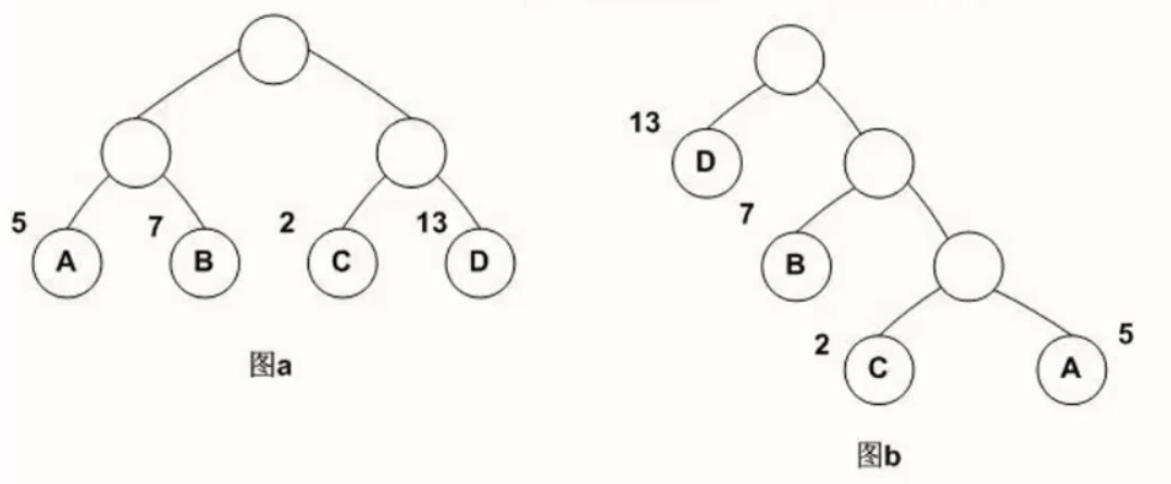
图a中的数字表示权重,图a是常见的二叉树,图b就是图a转换过的最优二叉树。
图a中权重表示重要程度,可以看出,D是最重要的,那么有这样一个规则:最重要的放在最前面,由此构造了图b的哈夫曼树。
它们的带权路径长度分别为:
图a:WPL = 5 * 2 + 7 * 2 + 2 * 2 +13 * 2 = 54
图b:WPL = 5 * 3 + 2 * 3 + 7 * 2 + 13 * 1 = 48
可见,图b的带权路径长度较小,我们可以证明图b就是哈夫曼树。
哈夫曼树的构造
例子:
有A B C D 四个词,数字表示词频,构造过程如下:
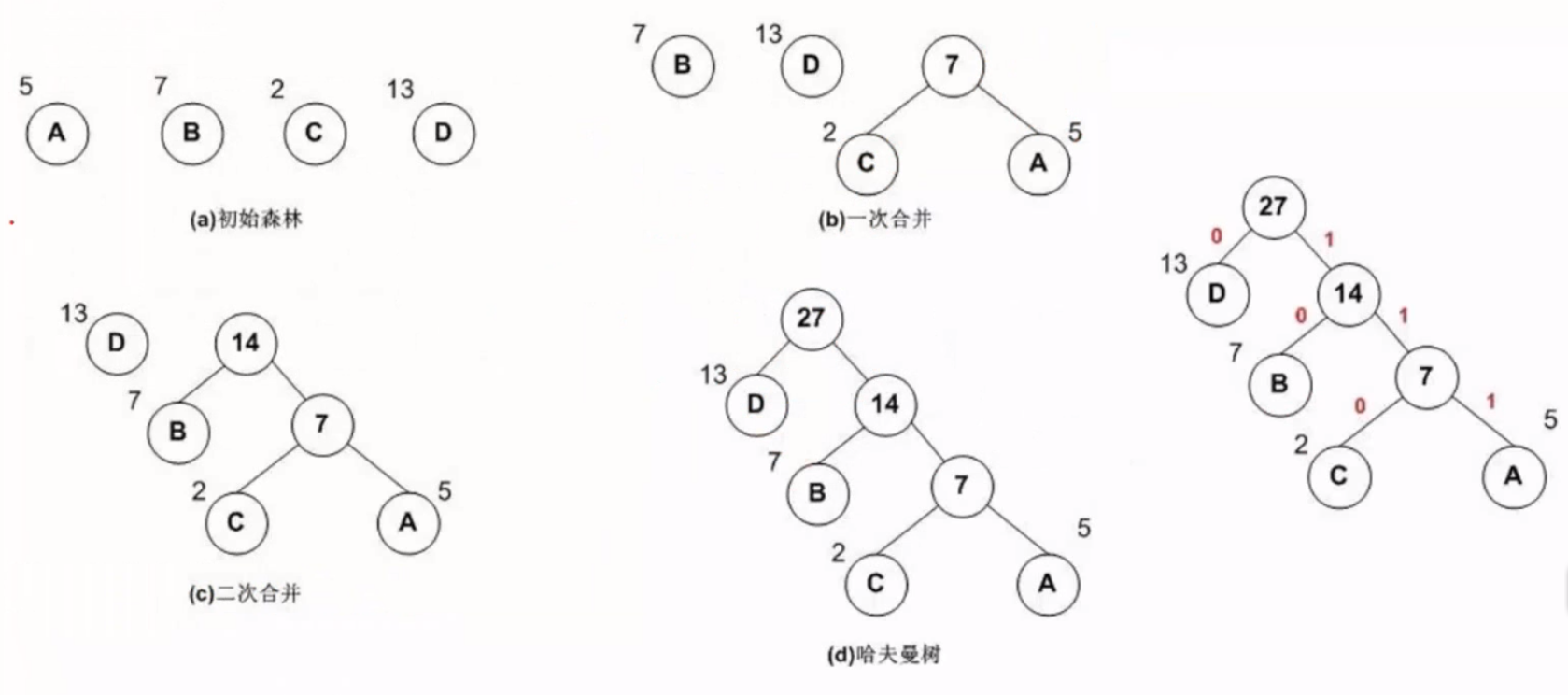
哈夫曼树编码
左子树为0,右子树为1

那么D编码为0,B编码为10,C编码为110,A编码为111。
Logistic Regression(逻辑斯蒂回归)
Logistic Regression的思想很简单,利用Sigmoid函数把任意值映射到(0,1)的区间上来实现分类问题(主要是二分类),
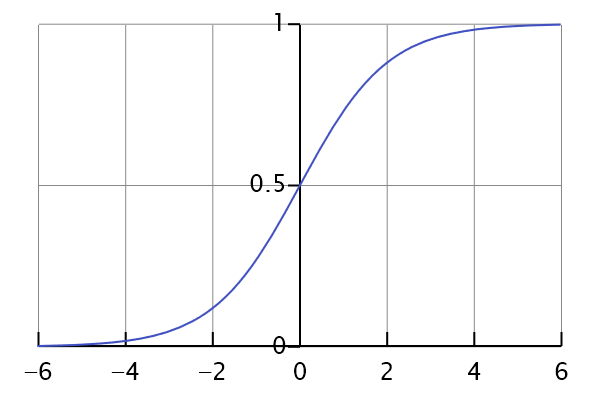
在这里不再详细阐述。
Softmax其实就是多分类的Logistic Regression,相当于把很多个Logistic Regression组合在一起。
Logistic Regression在这里的应用就是判断在哈夫曼树中走左子树还是右子树,其输出的值就是走某一条的概率。
Hierarchical Softmax

CBOW是已知上下文,估算当前词语的语言模型。其学习目标是最大化对数似然函数:
\mathcal{L}=\sum_{w \in \mathcal{C}} \log p(w | \operatorname{Context}(w))
其中,w表示语料库C中任意一个词。从上图可以看出,对于CBOW,
输入层是上下文的词语的词向量(什么!我们不是在训练词向量吗?不不不,我们是在训练CBOW模型,词向量只是个副产品,确切来说,是CBOW模型的一个参数。训练开始的时候,词向量是个随机值,随着训练的进行不断被更新)。
投影层对其求和,所谓求和,就是简单的向量加法。
输出层输出最可能的w。由于语料库中词汇量是固定的|C|个,所以上述过程其实可以看做一个多分类问题。给定特征,从|C|个分类中挑一个。
对于神经网络模型多分类,最朴素的做法是softmax回归:
h_{\theta}\left(x^{(i)}\right)=\left[ \begin{array}{c}{p\left(y^{(i)}=1 | x^{(i)} ; \theta\right)} \\ {p\left(y^{(i)}=2 | x^{(i)} ; \theta\right)} \\ {\vdots} \\ {p\left(y^{(i)}=k | x^{(i)} ; \theta\right)}\end{array}\right]=\frac{1}{\sum_{j=1}^{k} e^{\theta_{j}^{T} x^{(i)}}} \left[ \begin{array}{c}{e^{\theta_{1}^{T} x^{(i)}}} \\ {e^{\theta_{2}^{T} x^{(i)}}} \\ {\vdots} \\ {e^{\theta_{k}^{T} x^{(i)}}}\end{array}\right]
softmax回归需要对语料库中每个词语(类)都计算一遍输出概率并进行归一化,在几十万词汇量的语料上无疑是令人头疼的。
不用softmax怎么样?比如SVM中的多分类,我们都知道其多分类是由二分类组合而来的。
这是一种哈夫曼树结构,应用到word2vec中被作者称为Hierarchical Softmax:
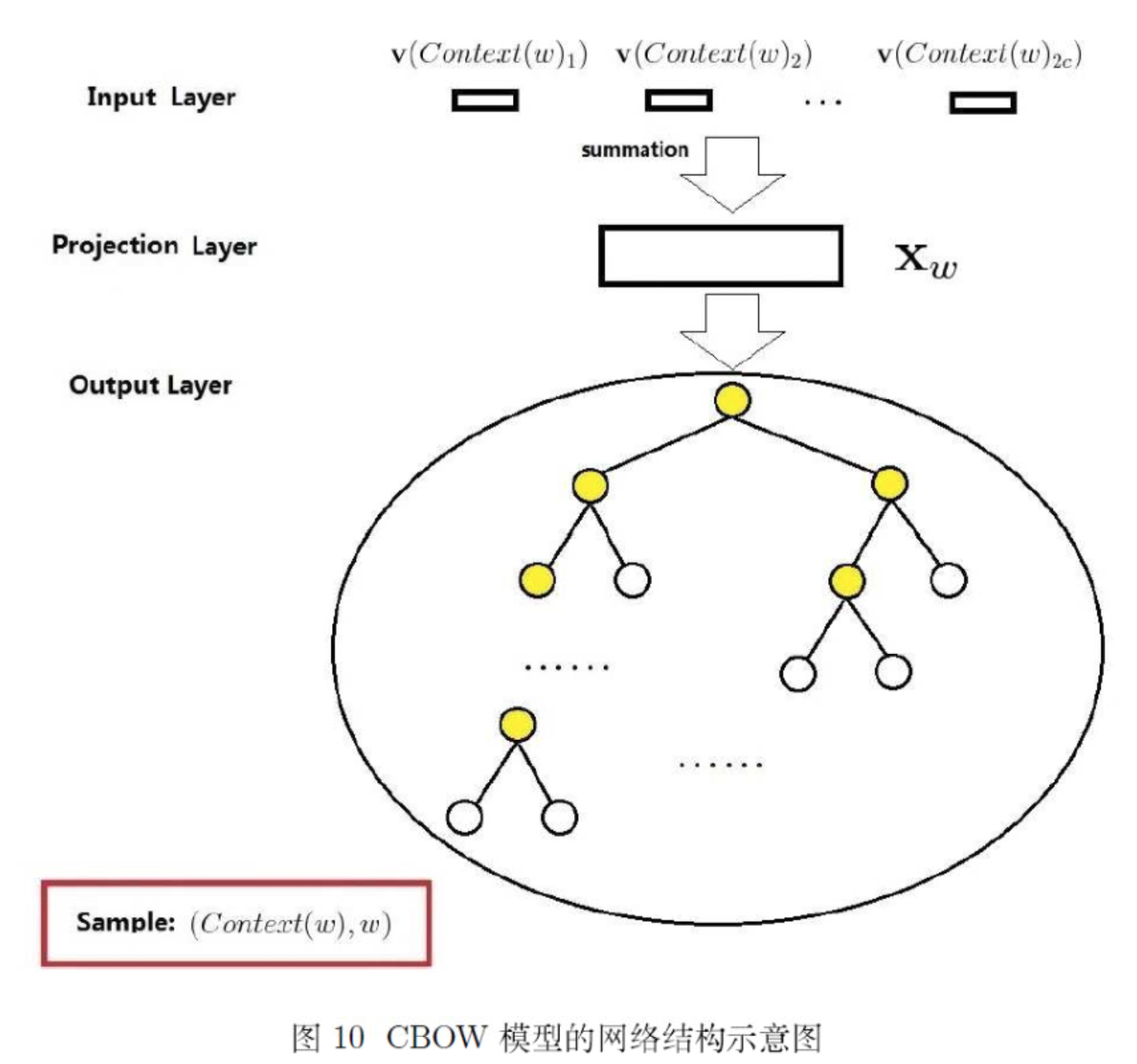
上图输出层的树形结构即为Hierarchical Softmax。
每个叶子节点代表语料库中的一个词,于是每个词语都可以被01唯一的编码,并且其编码序列对应一个事件序列,于是我们可以计算条件概率 p(w | C o n t e x t(w))
在开始计算之前,还是得引入一些符号:
1. p^{w} :从根结点出发到达w对应叶子结点的路径
2. l^{w} :路径中包含结点的个数
3. p_{1}^{w}, p_{2}^{w}, \cdots, p_{l^{w}}^{w} :路径 p^{w} 中的各个节点
4. d_{2}^{w}, d_{3}^{w}, \cdots, d_{l w}^{w} \in\{0,1\} :词w的编码, d_{j}^{w} 表示路径 p^{w} 第j个节点对应的编码(根节点无编码)
5. \theta_{1}^{w}, \theta_{2}^{w}, \cdots, \theta_{l^{w}-1}^{w} \in \mathbb{R}^{m} :路径 p^{w} 中非叶节点对应的参数向量
于是可以给出w的条件概率:
p(w | C o n t e x t(w))=\prod_{j=2}^{l^{w}} p\left(d_{j}^{w} | \mathbf{x}_{w}, \theta_{j-1}^{w}\right)
这是个简单明了的式子,从根节点到叶节点经过了 l^{w}-1 个节点,编码从下标2开始(根节点无编码),对应的参数向量下标从1开始(根节点为1)。
其中,每一项是一个逻辑斯谛回归:
p\left(d_{j}^{w} | \mathbf{x}_{w}, \theta_{j-1}^{w}\right)=\left\{\begin{array}{ll}{\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right),} & {d_{j}^{w}=0} \\ {1-\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right),} & {d_{j}^{w}=1}\end{array}\right.
考虑到d只有0和1两种取值,我们可以用指数形式方便地将其写到一起:
p\left(d_{j}^{w} | \mathbf{x}_{w}, \theta_{j-1}^{w}\right)=\left[\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right)\right]^{1-d_{j}^{w}} \cdot\left[1-\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right)\right]^{d^{w}}
我们的目标函数取对数似然:
\mathcal{L}=\sum_{w \in \mathcal{C}} \log p(w | C o n t e x t(w))
将 p(w | C o n t e x t(w)) 代入上式,有:
\mathcal{L}=\sum_{w \in \mathcal{C}} \log \prod_{j=2}^{l^{w}}\left\{\left[\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right)\right]^{1-d_{j}^{w}} \cdot\left[1-\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right)\right]^{d_{j}^{w}}\right\}
=\sum_{w \in \mathcal{C}} \sum_{j=2}^{l^{w}}\left\{\left(1-d_{j}^{w}\right) \cdot \log \left[\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right)\right]+d_{j}^{w} \cdot \log \left[1-\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right)\right]\right\}
这也很直白,连乘的对数换成求和。不过还是有点长,我们把每一项简记为:
\mathcal{L}(w, j)=\left(1-d_{j}^{w}\right) \cdot \log \left[\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right)\right]+d_{j}^{w} \cdot \log \left[1-\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right)\right]
怎么最大化对数似然函数呢?分别最大化每一项即可(这应该是一种近似,最大化某一项不一定使整体增大,具体收敛的证明还不清楚)。怎么最大化每一项呢?先求函数对每个变量的偏导数,对每一个样本,代入偏导数表达式得到函数在该维度的增长梯度,然后让对应参数加上这个梯度,函数在这个维度上就增长了。这种白话描述的算法在学术上叫随机梯度上升法,详见更规范的描述。
每一项有两个参数,一个是每个节点的参数向量 \theta_{j-1}^{w} ,另一个是输出层的输入 \mathbf{X}_{w} ,我们分别对其求偏导数:
\frac{\partial \mathcal{L}(w, j)}{\partial \theta_{j-1}^{w}}=\frac{\partial}{\partial \theta_{j-1}^{w}}\left\{\left(1-d_{j}^{w}\right) \cdot \log \left[\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right)\right]+d_{j}^{w} \cdot \log \left[1-\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right)\right]\right\}
因为sigmoid函数的导数有个很棒的形式:
\sigma^{\prime}(x)=\sigma(x)[1-\sigma(x)]
于是代入上上式得到:
\left(1-d_{j}^{w}\right)\left[1-\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right)\right] \mathbf{x}_{w}-d_{j}^{w} \sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right) \mathbf{x}_{w}
合并同类项得到:
\left[1-d_{j}^{w}-\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right)\right] \mathbf{x}_{w}
于是 \theta_{j-1}^{w}的更新表达式就得到了:
\theta_{j-1}^{w} :=\theta_{j-1}^{w}+\eta\left[1-d_{j}^{w}-\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right)\right] \mathbf{x}_{w}
其中, \eta 是学习率,通常取0-1之间的一个值。学习率越大训练速度越快,但目标函数容易在局部区域来回抖动。
再来 \mathbf{X}_{w} 的偏导数,注意到 \mathcal{L}(w, j)=\left(1-d_{j}^{w}\right) \cdot \log \left[\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right)\right]+d_{j}^{w} \cdot \log \left[1-\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right)\right] 中 \mathbf{X}_{w} 和 \theta_{j-1}^{w} 是对称的,所有直接将 \theta_{j-1}^{w} 的偏导数中的 \theta_{j-1}^{w} 替换为 \mathbf{X}_{w} ,得到关于 \mathbf{X}_{w} 的偏导数:
\frac{\partial \mathcal{L}(w, j)}{\partial \mathbf{x}_{w}}=\left[1-d_{j}^{w}-\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right)\right] \theta_{j-1}^{w}
于是 \mathbf{X}_{w} 的更新表达式也得到了。
不过 \mathbf{X}_{w} 是上下文的词向量的和,不是上下文单个词的词向量。怎么把这个更新量应用到单个词的词向量上去呢?word2vec采取的是直接将 \mathbf{X}_{w} 的更新量整个应用到每个单词的词向量上去:
\mathbf{v}(\widetilde{w}) :=\mathbf{v}(\widetilde{w})+\eta \sum_{j=2}^{l^{w}} \frac{\partial \mathcal{L}(w, j)}{\partial \mathbf{x}_{w}}, \quad \widetilde{w} \in \text { Context }(w)
其中, \mathbf{v}(\widetilde{w}) 代表上下文中某一个单词的词向量。我认为应该也可以将其平均后更新到每个词向量上去,无非是学习率的不同,欢迎指正。
感谢原作者

