[PnP]PnP问题之EPnP解法

接上一篇《[PnP] PnP问题之DLT解法》，本文介绍PnP的另一种常用解法EPnP。
EPnP也是ORB-SLAM2中使用的方法。
本文对EPnP方法进行了详细的推导，并基于Eigen库给出了实现。

• 与其他方法相比，EPnP方法的复杂度为O(n)。对于点对数量较多的PnP问题，非常高效。
• 核心思想是将三维点表示为4个控制点的组合；优化也只针对4个控制点，所以速度很快；在求解 Mx = 0时，最多考虑了4个奇异向量，因此精度也很高。

1. 理论推导

1.1 homogeneous barycentric coordinates （hb坐标）

本文符号与原文[1]中相同。点对数量为 n ，三维点的非齐次坐标为

\mathbf p_i,\ \ i=1,\cdots,n \\

利用上标 ^c 和 ^w 代表三维点在相机和世界坐标系下对应的坐标。EPnP引入了控制点，任何一个3D点都可以表示为四个控制点的线性组合。四个控制点的三维坐标记为

\mathbf c_j, \ \ j = 1,\cdots,4 \\

世界坐标系下的每个三维点可以由4个控制点表达为

\mathbf p^w_i = \sum_{j=1}^{4}{\alpha_{ij}\mathbf c_j^w} \ (1a)\\ \sum_{j=1}^{4}{\alpha_{ij}}=1 \ (1b)\\

式中的 \alpha_{ij} 称为(homogeneous barycentric coordinates)，本文称为hb坐标。(1)式还可写为，

\left[ {\begin{array}{*{20}{c}} {{\mathbf{p}}_i^w} \\ 1 \end{array}} \right] = \underbrace {\left[ {\begin{array}{*{20}{c}} {{\mathbf{c}}_1^w}&{{\mathbf{c}}_2^w}&{{\mathbf{c}}_3^w}&{{\mathbf{c}}_4^w} \\ 1&1&1&1 \end{array}} \right]}_{\mathbf{C}}\left[ {\begin{array}{*{20}{c}} {{\alpha _{i1}}} \\ {{\alpha _{i2}}} \\ {{\alpha _{i3}}} \\ {{\alpha _{i4}}} \end{array}} \right] \ (2) \\

实际上，3D点的齐次坐标被表示为控制点齐次坐标的线性组合。记待求解的相机与世界坐标系之间的相对位姿为 [\mathbf R | \mathbf t] ，控制点在相机坐标系下的坐标为

\mathbf c^c_j = [\mathbf R | \mathbf t]\left[ {\begin{array}{*{20}{c}} {{\mathbf{c}}_j^w} \\ 1 \end{array}} \right] \ (3)\\

那么，对于一个三维点，在相机坐标系下可表示为

\mathbf p_i^c = [\mathbf R | \mathbf t]\left[ {\begin{array}{*{20}{c}} {{\mathbf{p}}_i^w} \\ 1 \end{array}} \right] =\left[ {{\mathbf{R|t}}} \right]\left[ {\begin{array}{*{20}{c}} {\sum\limits_{j = 1}^4 {{\alpha _{ij}}{\mathbf{c}}_j^w} } \\ {\sum\limits_{j = 1}^4 {{\alpha _{ij}}} } \end{array}} \right] = \sum\limits_{j = 1}^4 {{\alpha _{ij}}{\mathbf{c}}_j^c} \ (4) \\

仔细看一下（4）式，发现在同一3D点在世界坐标系下的hb坐标与其在相机坐标系下的相同。这意味着，我们可以预先在世界坐标系下求取hb坐标 \alpha_{ij}，然后将其作为已知量拿到相机坐标系下使用。

1.2 如何选择控制点呢？

理论上，只要满足(2)式中的 \mathbf C 可逆，hb坐标就唯一，我们可以任意选择控制点。但是为了系统的稳定性，采用如下策略进行控制点的选取。第一个控制点选择在所有3D点的质心位置

{\mathbf{c}}_1^w{\text{ = }}\frac{1}{n}\sum\limits_{i = 1}^n {{\mathbf{p}}_i^w} \ (5) \\

其余点选择在数据的主方向上。具体操作如下，计算矩阵

{\mathbf{A}} = \left[ {\begin{array}{*{20}{c}} {{{\left( {{\mathbf{p}}_1^w} \right)}^T} - {{\left( {{\mathbf{c}}_1^w} \right)}^T}} \\ \cdots \\ {{{\left( {{\mathbf{p}}_n^w} \right)}^T} - {{\left( {{\mathbf{c}}_1^w} \right)}^T}} \end{array}} \right] \ (6) \\

计算 \mathbf A^T\mathbf A 的3个特征值为 \lambda_1, \lambda_2, \lambda_3 ，对应的特征向量为 \mathbf v_1, \mathbf v_2, \mathbf v_3 。那么剩余的三个控制点为

\left\{ \begin{gathered} {\mathbf{c}}_2^w = {\mathbf{c}}_1^w + \sqrt {\frac{{{\lambda _1}}}{n}} {{\mathbf{v}}_1} \hfill \\ {\mathbf{c}}_3^w = {\mathbf{c}}_1^w + \sqrt {\frac{{{\lambda _2}}}{n}} {{\mathbf{v}}_2} \hfill \\ {\mathbf{c}}_4^w = {\mathbf{c}}_1^w + \sqrt {\frac{{{\lambda _3}}}{n}} {{\mathbf{v}}_3} \hfill \\ \end{gathered} \right.\ (7) \\

上述操作实际上是找到点云的重心，以及点云的三个主方向，可以参考主成分分析(PCA)。

到目前为止，我们已知可以知道4个控制点在世界坐标系下的坐标 \mathbf c_j ，每一个3D点的hd坐标 \alpha_{ij} 。如果我们能把4个控制点在相机坐标系下的坐标求解出来，就可以计算出3D点在相机坐标系下的坐标，就可以求解出外参数 [\mathbf R | \mathbf t] ，下面就沿着这个思路展开。

1.3 控制点在相机坐标系下的坐标

1.3.1 解析求解

把相机投影模型搬出来

{\omega _i}\left[ {\begin{array}{*{20}{c}} {{{\mathbf{u}}_i}} \\ 1 \end{array}} \right] = {\mathbf{Kp}}_i^c = {\mathbf{K}}\sum\limits_{j = 1}^4 {{\alpha _{ij}}{\mathbf{c}}_j^c} = \left[ {\begin{array}{*{20}{c}} {{f_x}}&0&{{c_x}} \\ 0&{{f_y}}&{{c_y}} \\ 0&0&1 \end{array}} \right]\sum\limits_{j = 1}^4 {{\alpha _{ij}}\left[ {\begin{array}{*{20}{c}} {x_j^c} \\ {y_j^c} \\ {z_j^c} \end{array}} \right]} \ (8) \\

将（8）式展开，消掉最后一行，可得

\left\{ {\begin{array}{*{20}{l}} {\sum\limits_{j = 1}^4 {\left( {{\alpha _{ij}}{f_x}x_j^c + {\alpha _{ij}}\left( {{c_x} - {u_i}} \right)z_j^c} \right) = 0} } \\ {\sum\limits_{j = 1}^4 {\left( {{\alpha _{ij}}{f_y}y_j^c + {\alpha _{ij}}\left( {{c_y} - {v_i}} \right)z_j^c} \right) = 0} } \end{array}} \right. \ (9) \\

仔细看一哈，（9）式中hd坐标 \alpha_{ij} ，摄像机内参数 f_x 、 f_y 、 c_x 、 c_y ，以及2D点的坐标 u_i , v_i 都是已知变量，未知变量是4个控制点在摄像机坐标系下的坐标 x_j^c 、 y_j^c 和 z_i^c ，共计12个未知参数。一个点可以确定2个方程，把所有n 个点对都用上，可以形成一个线性方程

\mathbf M \mathbf x=0 \ (10) \\

其中， \mathbf x 就是待求的12个未知参数。 \mathbf M 的大小为 2n \times 12 。（10）式的解即为 \mathbf M 的零空间：

\mathbf x= \sum_{i = 1}^{N} \beta_i \mathbf v_i \ (11)\\

其中 \mathbf v_i 为 \mathbf M 的右奇异向量，对应的奇异值为0。具体解算方法为，求解 \mathbf M^T \mathbf M 的特征值和特征向量，特征值为0的特征向量即为 \mathbf v_i 。需要注意，不论有多少个点对， \mathbf M^T \mathbf M 的大小永远是 12\times12 。而计算\mathbf M^T \mathbf M的复杂度为 O(n) 。因此，算法的整体复杂度为 O(n)。

接下的问题就是如何确定（11）式的系数 \beta_i ，从而获得一个确定的解。首先， N 为多少个呢？原文[1]中说与点对的数量，控制点，相机焦距和噪声有关，所以考虑了 N=1,2,3,4 四种情况。下面，分别讨论这四种情况。

Case N=1

这是最简单的情况，（11）式这时变成了 \mathbf x = \beta \mathbf v。这时候把控制点在摄像机坐标系和世界坐标系的坐标联系起来：控制点间距在两种坐标系之下是相等的

{\left\| {{\mathbf{c}}_i^c - {\mathbf{c}}_j^c} \right\|^2} = {\left\| {{\mathbf{c}}_i^w - {\mathbf{c}}_j^w} \right\|^2} \ (12) \\

由此，引入一个约束。

{\left\| {\beta {{\mathbf{v}}^{\left[ i \right]}} - \beta {{\mathbf{v}}^{\left[ j \right]}}} \right\|^2} = {\left\| {{\mathbf{c}}_i^w - {\mathbf{c}}_j^w} \right\|^2} \ (13) \\

其中， \[{{{\mathbf{v}}^{\left[ i \right]}}}\] 表示 \mathbf v 中第 i 个控制点所占据的3个元素组成的向量。4个控制点，可以得到 \beta 的一个闭式解

\beta = \frac{{\sum\limits_{\{ i,j\} \in [1:4]} {\left\| {{{\mathbf{v}}^{\left[ i \right]}} - {{\mathbf{v}}^{\left[ j \right]}}} \right\| \cdot \left\| {{\mathbf{c}}_i^w - {\mathbf{c}}_j^w} \right\|} }}{{\sum\limits_{\{ i,j\} \in [1:4]} {{{\left\| {{{\mathbf{v}}^{\left[ i \right]}} - {{\mathbf{v}}^{\left[ j \right]}}} \right\|}^2}} }} \ (14) \\

Case N=2

此时，（11）式变为 x=\beta_1 \mathbf v_1 + \beta_2 \mathbf v_2 ，带入到（12）式

{\left\| {\left( {{\beta _1}{\mathbf{v}}_1^{\left[ i \right]} + {\beta _2}{\mathbf{v}}_2^{\left[ i \right]}} \right) - \left( {{\beta _1}{\mathbf{v}}_1^{\left[ j \right]} + {\beta _2}{\mathbf{v}}_2^{\left[ j \right]}} \right)} \right\|^2} = {\left\| {{\mathbf{c}}_i^w - {\mathbf{c}}_j^w} \right\|^2} \ (15) \\

将（15）展开

\begin{array}{*{20}{c}} {||{\beta _1}\underbrace {\left( {{\mathbf{v}}_1^{[i]} - {\mathbf{v}}_1^{[j]}} \right)}_{{{\mathbf{S}}_1}}{\text{ + }}{\beta _2}\underbrace {\left( {{\mathbf{v}}_2^{[i]} - {\mathbf{v}}_2^{[j]}} \right)}_{{{\mathbf{S}}_2}}|{|^2} = \underbrace {{{\left\| {{\mathbf{c}}_i^w - {\mathbf{c}}_j^w} \right\|}^2}}_c} \\ \Downarrow \\ {{\beta _1}^2{{\mathbf{S}}_1}^T{{\mathbf{S}}_1} + 2{\beta _1}{\beta _2}{{\mathbf{S}}_1}^T{{\mathbf{S}}_2} + {\beta _2}^2{{\mathbf{S}}_2}^T{{\mathbf{S}}_2} = c} \end{array} \ (16) \\

引入三个中间变量

{\beta _{11}} = {\beta _1}^2,{\beta _{22}} = {\beta _{22}}^2,{\beta _{12}} = {\beta _1}{\beta _2} \ (17) \\

（16）式就变成了线性方程（中间变量法，可以将非线性方程转换成线性方程解算）。4个控制点可以构造出6个线性方程，组成

\mathbf L \bm\beta = \bm \rho \ (18) \\

其中， \bm {\beta} = [\beta_{11}, \beta_{12}, \beta_{22}]^T ，\mathbf L 中为（16）式左边的系数大小为 6\times 3 ， \bm{\rho} 中为（16）式右边的系数，大小为 6\times 1 。解出 \bm \beta 后，再结合（17）式，可以获得两组 \beta_1,\ \beta_2 的解。再加上一个条件，控制点在摄像机的前端，即 \bm{c}_j^c 的 z 分量要大于0，从而\beta_1,\ \beta_2唯一确定。

Case N=3

与Case N=2 的解法相同。这里的 \bm \beta = [\beta_{11}, \beta_{12},\beta_{13}, \beta_{22}, \beta_{23}, \beta_{33}]^T ， \mathbf L的大小为 6\times6 。

Case N =4

再次使用Case N=2 的解法试一下，此时 \bm \beta = [\beta_{11}, \beta_{12}, \beta_{13}, \beta_{14}, \beta_{22}, \beta_{23}, \beta_{24}, \beta_{33}, \beta_{34}, \beta_{44}]^T ， \mathbf L 的大小为 6\times 10 。显然，无法得到唯一解。这次，就不能直接使用Case N=2，N=3 的解法了。因为，方程的数量少于待求解变量。看一下中间变量法，引入中间变量的同时，也增加了变量的个数。比如，Case N=3 的时候，引入中间变量后，变量个数由3个变成了6个。多出了3个变量 \beta_{ab} 。原文[1]提到，再引入约束，使用"Reinearization"的方法求解。（这个我也没看明白额）

实际上，OpenCV中开源代码并没按照上述4个Case中的方法去求解，而是采用了近似的解法，具体的可以去看一下源码。但是为什么可以近似，我没搞太明白。我自己的实现目前也是按照OpenCV的方法去解的。

至此， \beta_1 \sim \beta_4 的初值求解完毕。

1.3.2 参数 \bm \beta 优化

下面，优化 \bm \beta 。需要注意，这里的 \bm \beta = [\beta_1, \beta_2, \beta_2, \beta_3]^T 。 N=1,2,3 的情况中，剩余的 \beta 直接补0。同样，还是优化两个坐标系下控制点间距的差。

\begin{gathered} {{\bm{\beta }}^*} = \mathop {\arg \min }\limits_{\bm{\beta }} \sum\limits_{(i,j),s.t.i < j} {{{\left\| {Error_{i,j}({\bm{\beta }})} \right\|}^2}} \hfill \\ Error_{i,j}({\bm{\beta }}) = \underbrace {{{\left\| {{\mathbf{c}}_i^c - {\mathbf{c}}_j^c} \right\|}^2}}_{cc} - \underbrace {{{\left\| {{\mathbf{c}}_i^w - {\mathbf{c}}_j^w} \right\|}^2}}_{cw} \hfill \\ \end{gathered} \ (19)\\

其中，

\begin{aligned} cc & = {\left\| {\left( {{\beta _1}{\mathbf{v}}_1^{[i]} + {\beta _2}{\mathbf{v}}_2^{[i]} + {\beta _3}{\mathbf{v}}_3^{[i]} + {\beta _4}{\mathbf{v}}_4^{[i]}} \right) - \left( {{\beta _1}{\mathbf{v}}_1^{[j]} + {\beta _2}{\mathbf{v}}_2^{[j]} + {\beta _3}{\mathbf{v}}_3^{[j]} + {\beta _4}{\mathbf{v}}_4^{[j]}} \right)} \right\|^2} \\ & {\text{ = }}||{\beta _1}\underbrace {\left( {{\mathbf{v}}_1^{[i]} - {\mathbf{v}}_1^{[j]}} \right)}_{{{\mathbf{S}}_1}} + {\beta _2}\underbrace {\left( {{\mathbf{v}}_2^{[i]} - {\mathbf{v}}_2^{[j]}} \right)}_{{{\mathbf{S}}_2}} + {\beta _3}\underbrace {\left( {{\mathbf{v}}_3^{[i]} - {\mathbf{v}}_3^{[j]}} \right)}_{{{\mathbf{S}}_3}} + {\beta _4}\underbrace {\left( {{\mathbf{v}}_4^{[i]} - {\mathbf{v}}_4^{[j]}} \right)}_{{{\mathbf{S}}_4}}|{|^2} \\ & {\text{ = }}{\beta _1}^2{{\mathbf{S}}_1}^T{{\mathbf{S}}_1}{\text{ + }}{\beta _1}{\beta _2}{{\mathbf{S}}_1}^T{{\mathbf{S}}_2}{\text{ + }}{\beta _1}{\beta _3}{{\mathbf{S}}_1}^T{{\mathbf{S}}_3}{\text{ + }}{\beta _1}{\beta _4}{{\mathbf{S}}_1}^T{{\mathbf{S}}_4} \\ & + {\beta _1}{\beta _2}{{\mathbf{S}}_2}^T{{\mathbf{S}}_1}{\text{ + }}{\beta _2}^2{{\mathbf{S}}_2}^T{{\mathbf{S}}_2}{\text{ + }}{\beta _2}{\beta _3}{{\mathbf{S}}_2}^T{{\mathbf{S}}_3}{\text{ + }}{\beta _2}{\beta _4}{{\mathbf{S}}_2}^T{{\mathbf{S}}_4} \\ & + {\beta _1}{\beta _3}{{\mathbf{S}}_3}^T{{\mathbf{S}}_1}{\text{ + }}{\beta _2}{\beta _3}{{\mathbf{S}}_3}^T{{\mathbf{S}}_2}{\text{ + }}{\beta _3}^2{{\mathbf{S}}_3}^T{{\mathbf{S}}_3}{\text{ + }}{\beta _3}{\beta _4}{{\mathbf{S}}_3}^T{{\mathbf{S}}_4} \\ & + {\beta _1}{\beta _4}{{\mathbf{S}}_4}^T{{\mathbf{S}}_1}{\text{ + }}{\beta _2}{\beta _4}{{\mathbf{S}}_4}^T{{\mathbf{S}}_2}{\text{ + }}{\beta _3}{\beta _4}{{\mathbf{S}}_4}^T{{\mathbf{S}}_3}{\text{ + }}{\beta _4}^2{{\mathbf{S}}_4}^T{{\mathbf{S}}_4} \\ & {\text{ = }}{\beta _1}^2{{\mathbf{S}}_1}^T{{\mathbf{S}}_1}{\text{ + 2}}{\beta _1}{\beta _2}{{\mathbf{S}}_1}^T{{\mathbf{S}}_2}{\text{ + 2}}{\beta _1}{\beta _3}{{\mathbf{S}}_1}^T{{\mathbf{S}}_3}{\text{ + 2}}{\beta _1}{\beta _4}{{\mathbf{S}}_1}^T{{\mathbf{S}}_4} \\ & {\text{ + }}{\beta _2}^2{{\mathbf{S}}_2}^T{{\mathbf{S}}_2} + 2{\beta _2}{\beta _3}{{\mathbf{S}}_2}^T{{\mathbf{S}}_3} + 2{\beta _2}{\beta _4}{{\mathbf{S}}_2}^T{{\mathbf{S}}_4} \\ & {\text{ + }}{\beta _3}^2{{\mathbf{S}}_3}^T{{\mathbf{S}}_3}{\text{ + 2}}{\beta _3}{\beta _4}{{\mathbf{S}}_3}^T{{\mathbf{S}}_4} \\ & {\text{ + }}{\beta _4}^2{{\mathbf{S}}_4}^T{{\mathbf{S}}_4} \\ \end{aligned} \ (20)\\

下面，利用Gauss-Newton求解式（19）。首先求解 \[Error({\bm{\beta }})\] 相对于 \bm \beta 的雅克比

\begin{aligned} {{\mathbf{J}}_{i,j}} & = \frac{{\partial \left[ {Erro{r_{i,j}}({\mathbf{\beta }})} \right]}}{{\partial {\mathbf{\beta }}}} \\ & {\text{ = }}{\left[ {\begin{array}{*{20}{c}} {2{\beta _1}{{\mathbf{S}}_1}^T{{\mathbf{S}}_1} + 2{\beta _2}{{\mathbf{S}}_1}^T{{\mathbf{S}}_2}{\text{ + }}2{\beta _3}{{\mathbf{S}}_1}^T{{\mathbf{S}}_3} + 2{\beta _4}{{\mathbf{S}}_1}^T{{\mathbf{S}}_4}} \\ {{\text{2}}{\beta _1}{{\mathbf{S}}_1}^T{{\mathbf{S}}_2}{\text{ + }}2{\beta _2}{{\mathbf{S}}_2}^T{{\mathbf{S}}_2} + 2{\beta _3}{{\mathbf{S}}_2}^T{{\mathbf{S}}_3} + 2{\beta _4}{{\mathbf{S}}_2}^T{{\mathbf{S}}_4}} \\ {{\text{2}}{\beta _1}{{\mathbf{S}}_1}^T{{\mathbf{S}}_3} + 2{\beta _2}{{\mathbf{S}}_2}^T{{\mathbf{S}}_3}{\text{ + 2}}{\beta _3}{{\mathbf{S}}_3}^T{{\mathbf{S}}_3}{\text{ + 2}}{\beta _4}{{\mathbf{S}}_3}^T{{\mathbf{S}}_4}} \\ {{\text{2}}{\beta _1}{{\mathbf{S}}_1}^T{{\mathbf{S}}_4} + 2{\beta _2}{{\mathbf{S}}_2}^T{{\mathbf{S}}_4}{\text{ + 2}}{\beta _3}{{\mathbf{S}}_3}^T{{\mathbf{S}}_4}{\text{ + 2}}{\beta _4}{{\mathbf{S}}_4}^T{{\mathbf{S}}_4}} \end{array}} \right]^{\text{T}}} \\ \end{aligned} \ (21)\\

将六个小雅克比 \bm J_{i,j} 合成为 6\times 4 的大雅克比

{\mathbf{J}} = \left[ {\begin{array}{*{20}{l}} {{{\mathbf{J}}_{1,2}}} \\ {{{\mathbf{J}}_{1,3}}} \\ {{{\mathbf{J}}_{1,4}}} \\ {{{\mathbf{J}}_{2,3}}} \\ {{{\mathbf{J}}_{2,4}}} \\ {{{\mathbf{J}}_{3,4}}} \end{array}} \right] \\

记残差为

{\mathbf{r}} = \left[ {\begin{array}{*{20}{l}} {Erro{r_{1,2}}\left( {\bm{\beta }} \right)} \\ {Erro{r_{1,3}}\left( {\bm{\beta }} \right)} \\ {Erro{r_{1,4}}\left( {\bm{\beta }} \right)} \\ {Erro{r_{2,3}}\left( {\bm{\beta }} \right)} \\ {Erro{r_{2,4}}\left( {\bm{\beta }} \right)} \\ {Erro{r_{3,4}}\left( {\bm{\beta }} \right)} \end{array}} \right] \\

那么，增量方程为

{{\mathbf{J}}^T}{\mathbf{J}}\delta {\mathbf{\beta }} = - {{\mathbf{J}}^T}{\mathbf{r}} \ (22) \\

更新方程

{\bm{\beta }} = {\bm{\beta }} + \delta {\bm{\beta }} \ (23)\\

迭代计算。上面其实就是标准的最小二乘优化，高博十四讲中就有详细的介绍。

至此， \bm \beta 就解完了。那么，控制点在摄像机坐标系下的坐标\mathbf c_j 也全部解出来了。下面开始求解 [\mathbf R | \mathbf t] 。

1.4 求解 [\mathbf R | \mathbf t]

首先，根据控制点 \mathbf c_j ，将所有的3D点在摄像机坐标系下的坐标 \mathbf p_i^c 恢复出来。我就知道所有3D-3D的匹配了。于是，就变成了已知匹配的ICP问题。这个求解方法在高博的十四讲中也有详细的介绍。具体的解法如下。

Step 1. 计算质心坐标

\mathbf p_c^c=\frac {1}{n}\sum_{i=1}^n \mathbf p_i^c \\

\mathbf p_c^w=\frac {1}{n}\sum_{i=1}^n \mathbf p_i^w \\

Step 2. 去除质心

{{\mathbf{P}}^c}{\text{ = }}\left[ {\begin{array}{*{20}{c}} {({\mathbf{p}}_1^c)^T - ({\mathbf{p}}_c^c})^T \\ \cdots \\ {({\mathbf{p}}_n^c)^T - ({\mathbf{p}}_c^c})^T \end{array}} \right] \\

{{\mathbf{P}}^w}{\text{ = }}\left[ {\begin{array}{*{20}{c}} { ({\mathbf{p}}_1^w)^T - ({\mathbf{p}}_c^w})^T \\ \cdots \\ {({\mathbf{p}}_n^w)^T - ({\mathbf{p}}_c^w})^T \end{array}} \right] \\

Step 3. 计算 \mathbf R

{\mathbf{W}} = {\left( {{{\mathbf{P}}^c}} \right)^T}{{\mathbf{P}}^w} \\

\left[ {{\mathbf{U \Sigma V}}} \right] = SVD\left( {\mathbf{W}} \right) \\

{\mathbf{R}}{\text{ = }}{\mathbf{U}}{{\mathbf{V}}^T}\\

如果 |\mathbf R | < 0 ， \mathbf R(2,:) = - \mathbf R(2,:) 。

Step 4. 计算平移 \mathbf t

{\mathbf{t}} = {\mathbf{p}}_c^c - {\mathbf{Rp}}_c^w \\

请注意，因为 \bm \beta 有四种情况的解。所以，这里的 \mathbf {[R|t]} 实际上计算了四次，最终选择重投影误差最小的解。

2. 工程实现&实验

2.1 实现

我这里基于Eigen进行了实现，与OpenCV库里的EPnP实现稍有不同。详细代码请见：

2.2 实验

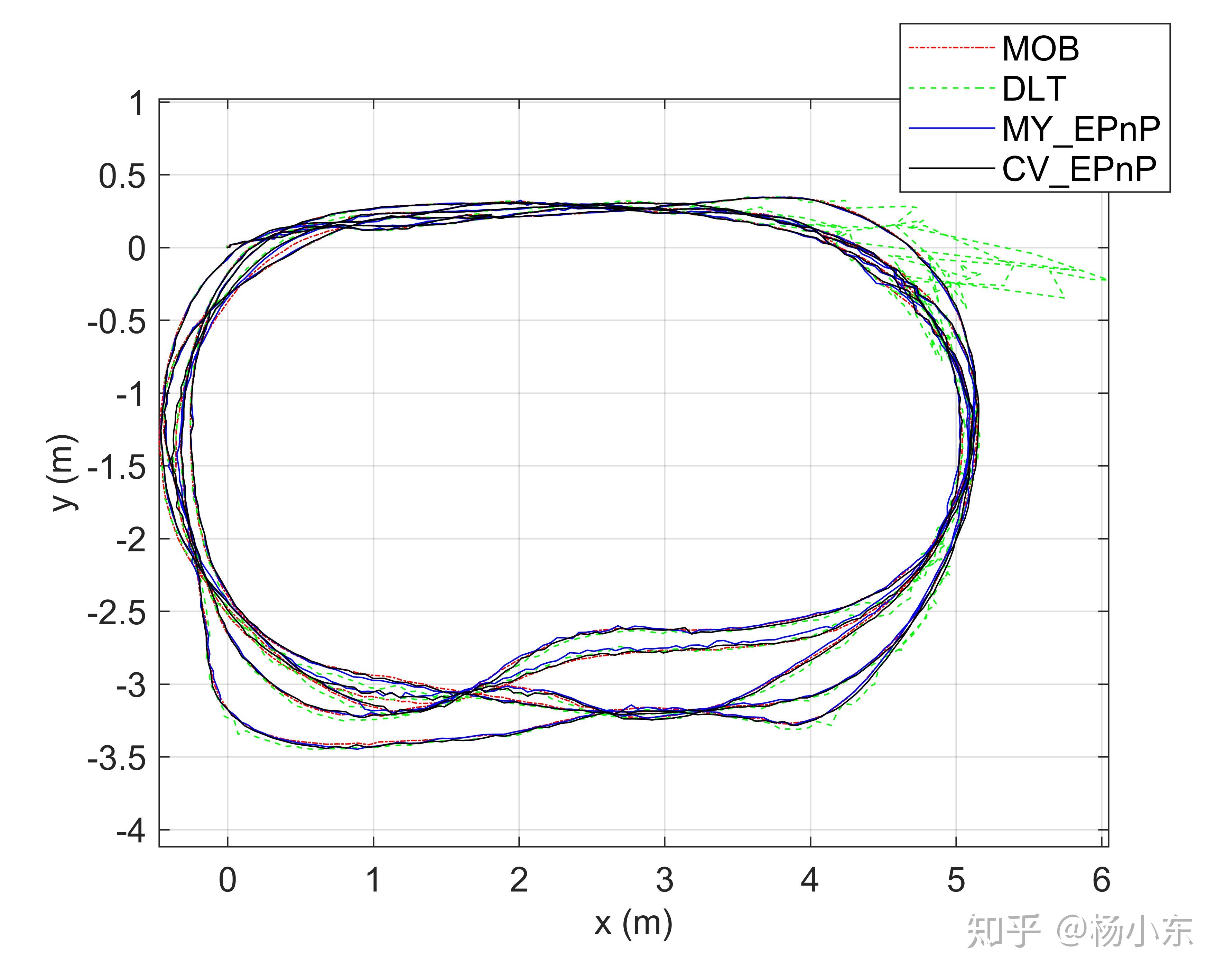
实验与上一篇《[PnP] PnP问题之DLT解法》相同，自己实现的EPnP（MY_EPnP）以及OpenCV自带的EnP（CV_EPnP）塞到了ORB-SLAM2的前端，与Motion Only BA（MOB）的方法和DLT的方法进行比较，结果如下图。

EPnP的结果已经十分接近MOB的方法了，轨迹也比较的平滑。不像DLT那样有很大的波动。（DLT的轨迹之所以波动比较大，可能是因为计算Ax=0的时候零空间只考虑了1个奇异向量，而EPnP最多考虑了4个奇异向量，而且还加了优化。）

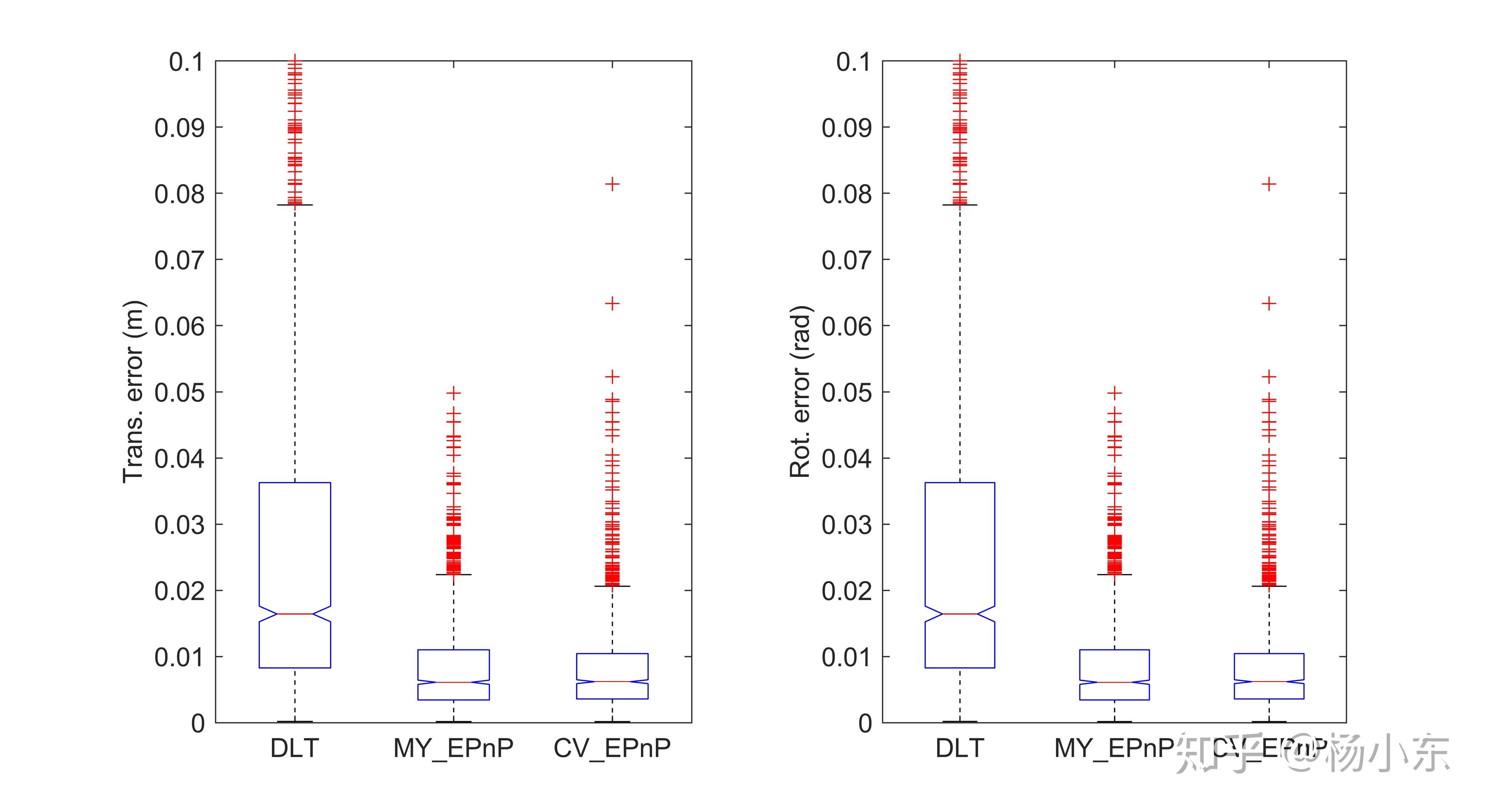
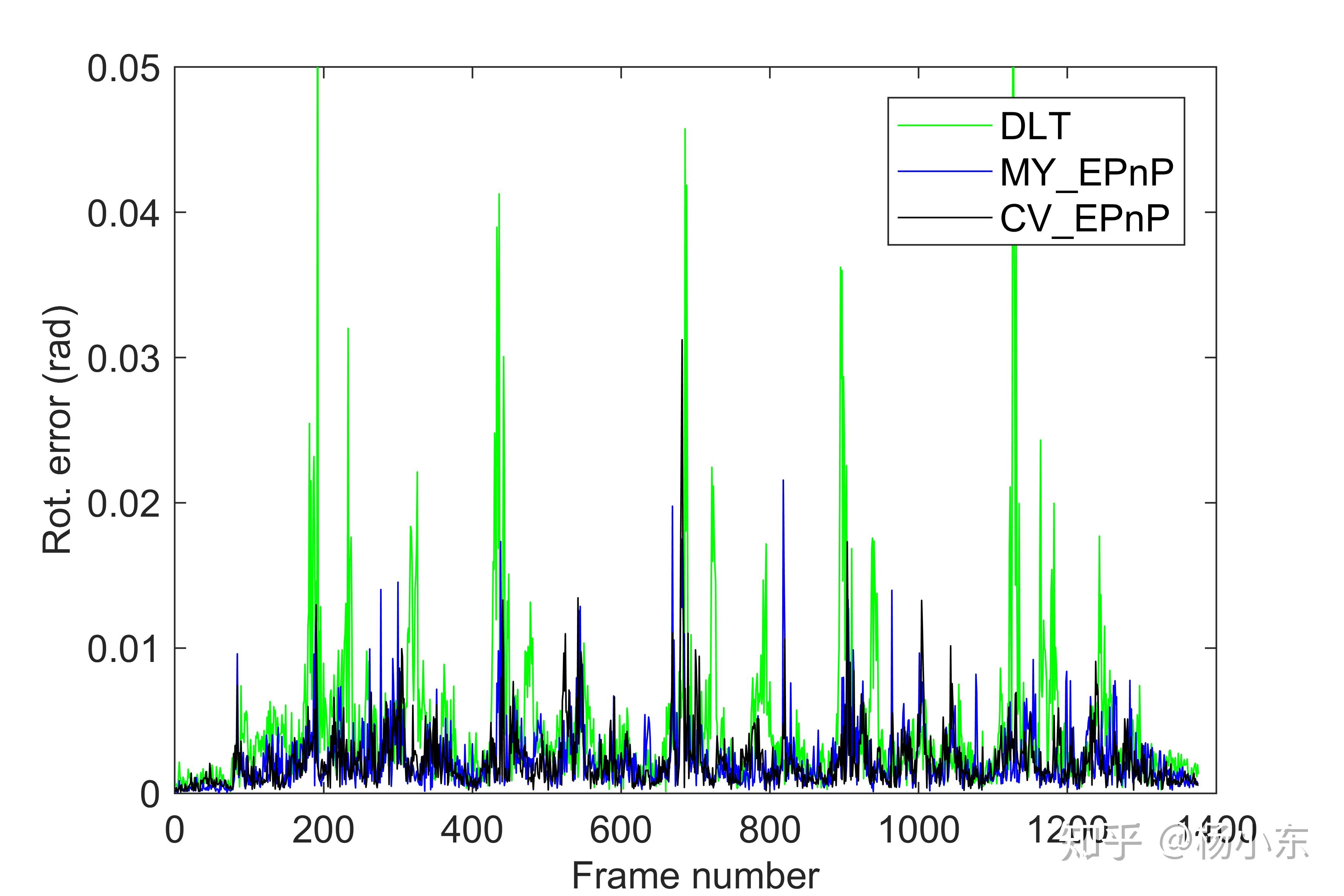
从平移和旋转误差来看，EPnP的精度明显高于DLT方法。

运行时间上，EPnP方法比DLT稍慢，在配置为Intel i7-8700, Ubuntu 16.04的电脑上，计算200~300个点对，MY_EPnP运算时间为 0.0852± 0.0153ms，CV_EPnP的运算时间为0.1202±0.0198 ms。

MY_EPnP与CV_EPnP的在精度、稳定性和运行时间三个方面都非常接近，可以说明自己编写的EPnp功能是正确的。在运算时间方面，MY_EPnP稍优于CV_EPnP方法。在精度方面，CV_EPnP稍优于MY_EPnP。

参考资料

[1] Lepetit, V.; Moreno-Noguer, F.; Fua, P. Epnp: Efficient perspective-n-point camera pose estimation. International Journal of Computer Vision 2009, 81, 155-166.

[2] [原创]深入EPnP算法

[3] 【泡泡机器人公开课】第三十九课：PnP算法简介与代码解析

[4] OpenCV EPnP实现

----更多SLAM文章----

杨小东：[PnP] PnP问题之DLT解法

杨小东：[ORB-SLAM2]卡方分布(Chi-squared)外点(outlier)剔除

杨小东：[ORB-SLAM2] ORB特征提取策略对ORB-SLAM2性能的影响

杨小东：[PR-3]ArUco EKF SLAM 扩展卡尔曼SLAM

杨小东：[PR-2] PF 粒子滤波/蒙特卡罗定位

----相关代码----