「Python与地震工程」复模态分析
背景图:1906年4月地震和火灾后的美国圣弗朗西斯科
原理
运动方程的降阶处理
多自由度体系的运动方程(式中粗体为矩阵或向量)
\boldsymbol{M\ddot u + C\dot u + Ku = p}
增加恒等式
\boldsymbol{M\dot u} - \boldsymbol{M\dot u} = \boldsymbol{0}
写成广义矩阵的形式
\left[ \begin{matrix} \boldsymbol{C}& \boldsymbol{M}\\ \boldsymbol{M}& \boldsymbol{0}\\ \end{matrix} \right] \left\{ \begin{array}{c} \boldsymbol{\dot{u}}\\ \boldsymbol{\ddot{u}}\\ \end{array} \right\} +\left[ \begin{matrix} \boldsymbol{K}& \boldsymbol{0}\\ \boldsymbol{0}& -\boldsymbol{M}\\ \end{matrix} \right] \left\{ \begin{array}{c} \boldsymbol{u}\\ \boldsymbol{\dot{u}}\\ \end{array} \right\} =\left\{ \begin{array}{c} \boldsymbol{P}\\ \boldsymbol{0}\\ \end{array} \right\}
令
\boldsymbol{x}=\left\{ \begin{array}{c} \boldsymbol{u}\\ \boldsymbol{\dot{u}}\\ \end{array} \right\}
运动方程可改写为
{\boldsymbol{A\dot x}} + {\boldsymbol{B x}} = {\boldsymbol{f}}
其中
\boldsymbol{A} = \left[ \begin{matrix} \boldsymbol{C}& \boldsymbol{M}\\ \boldsymbol{M}& \boldsymbol{0}\\ \end{matrix} \right]
\boldsymbol{B} = \left[ \begin{matrix} \boldsymbol{K}& \boldsymbol{0}\\ \boldsymbol{0}& -\boldsymbol{M}\\ \end{matrix} \right]
\boldsymbol{f} = \left\{ \begin{array}{c} \boldsymbol{P}\\ \boldsymbol{0}\\ \end{array} \right\}
复模态分析
自由振动方程
{\boldsymbol{A\dot x}} + {\boldsymbol{B x}} = {\boldsymbol{0}}
令 \boldsymbol{u} = \boldsymbol{\phi}e^{\lambda t}
\boldsymbol{x}=\left\{ \begin{array}{c} \boldsymbol{u}\\ \boldsymbol{\dot{u}}\\ \end{array} \right\} =\left\{ \begin{array}{c} \boldsymbol{\phi }\\ \lambda \boldsymbol{\phi }\\ \end{array} \right\} e^{\lambda t}=\boldsymbol{\varphi }e^{\lambda t}
整理得广义特征值问题
\lambda {\boldsymbol{A}}\boldsymbol{\varphi}=-{\boldsymbol{B}}\boldsymbol{\varphi}
所求得特征值及特征向量均为复数,前 N 个特征值
\lambda_j = -a_j + \mathrm{i} \: b_j \quad \cdots \quad j=1,2,\cdots,N
后 N 个特征值与前 N 个特征值共轭
\lambda_{j+N} = -a_j - \mathrm{i} \: b_j \quad \cdots \quad j=1,2,\cdots,N
复特征值的实部和虚部有物理意义
\lambda_j = -\zeta_j \omega_j + \mathrm{i} \:\omega_j \sqrt{1-\zeta_j^2} \quad \cdots \quad j=1,2,\cdots,N
\lambda_{j+N} = -\zeta_j \omega_j - \mathrm{i} \:\omega_j \sqrt{1-\zeta_j^2} \quad \cdots \quad j=1,2,\cdots,N
模态圆频率
\omega_j = \sqrt{a_j^2+b_j^2}
模态阻尼比
\zeta _j = \frac{a_j}{\sqrt{a_j^2+b_j^2}}
程序代码
import numpy as np
import scipy.linalg as spl
import matplotlib.pyplot as plt
plt.style.use("ggplot")
plt.rcParams['font.sans-serif'] = ['Microsoft Yahei']
plt.rcParams['axes.unicode_minus'] = False
import sys
np.set_printoptions(precision=4, threshold=sys.maxsize,
linewidth=150)
class MDOF():
def __init__(self, m, k, c, zeta=0.05) -> None:
self.m = m
self.k = k
self.c = c
self.zeta = zeta
self.ndof = len(m)
def build_matrix(self, damp_mat="D", i=1, j=2):
'''
建立质量、刚度、阻尼矩阵和荷载向量\\
参数含义:
damp_mat: 固有阻尼矩阵的建立方法。“D”为直接构造(默认),“R”为瑞利阻尼。
i,j: 确定瑞利阻尼系数的两阶振型序号。默认i=1, j=2。
'''
self.M = np.diag(self.m)
k1 = np.zeros_like(self.k)
k1[:-1] = self.k[1:]
self.K = np.diag(self.k+k1) + np.diag(-self.k[1:],1) + np.diag(-self.k[1:],-1)
c1 = np.zeros_like(self.c)
c1[:-1] = self.c[1:]
self.C = np.diag(self.c+c1) + np.diag(-self.c[1:],1) + np.diag(-self.c[1:],-1)
self.E = np.ones(self.ndof)
if self.zeta > 0:
self.mode_analyze()
if damp_mat == "D":
M_n = np.diag(self.phi.T.dot(self.M).dot(self.phi))
C_ = np.diag(2.0*self.zeta*self.omega/M_n)
self.C += self.M.dot(self.phi).dot(C_).dot(self.phi.T).dot(self.M)
elif damp_mat == "R":
w_i, w_j = self.omega[i-1], self.omega[j-1]
a_0, a_1 = self.zeta*2.0*w_i*w_j/(w_i+w_j), self.zeta*2.0/(w_i+w_j)
self.C += a_0*self.M + a_1*self.K
else:
self.C += np.zeros_like(self.M)
def mode_analyze(self, check_orthogonality=False):
omega2, self.phi = spl.eigh(self.K, self.M)
self.omega = np.sqrt(omega2)
self.period = 2.0*np.pi/self.omega
# 验证正交性
if check_orthogonality:
print("正交性验证")
print("ΦMΦ:")
print(self.phi.T @ self.M @ self.phi)
print("ΦKΦ:")
print(self.phi.T @ self.K @ self.phi)
def complex_mode_analyze(self, check_orthogonality=False):
self.O = np.zeros((self.ndof, self.ndof))
self.A = np.block( [
[self.C, self.M],
[self.M, self.O] ] )
self.B = np.block( [
[self.K, self.O],
[self.O,-self.M] ] )
lamda, Phi = spl.eig(-self.B, self.A)
# eig 默认将复特征值按模从大到小排列,按结构分析惯例将其逆序排列
self.lamda = lamda[::-1]
self.Phi = np.flip(Phi, axis=1)
# 计算自振圆频率及阻尼比
tmp = self.lamda[::2]
self.omega = abs(tmp)
self.zeta = -tmp.real/self.omega
# 验证正交性
if check_orthogonality:
print("正交性验证")
print("ΦAΦ:")
print(self.Phi.T @ self.A @ self.Phi)
print("ΦBΦ:")
print(self.Phi.T @ self.B @ self.Phi)
if __name__ == '__main__':
ndof = 3
m = np.ones(ndof)
k = 1600.0*m
c = np.zeros(ndof)
zeta = 0.05 # 固有阻尼比
mdof = MDOF(m, k, c, zeta)
mdof.build_matrix("D")
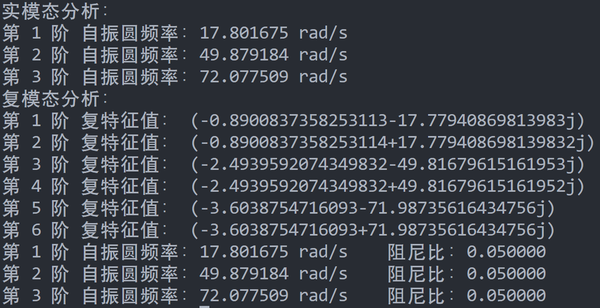
print("实模态分析:")
mdof.mode_analyze()
for i in range(ndof):
print("第 %d 阶 自振圆频率:%f rad/s"%(i+1, mdof.omega[i]))
print("复模态分析:")
mdof.complex_mode_analyze(True)
for i in range(ndof*2):
print("第 %d 阶 复特征值:"%(i+1), mdof.lamda[i])
for i in range(ndof):
print("第 %d 阶 自振圆频率:%f rad/s 阻尼比:%f"%(i+1, mdof.omega[i], mdof.zeta[i]))
结果
实模态与复模态分析得到的自振圆频率完全一致。
通过复模态分析,证实了所构造的阻尼矩阵实现了预设的阻尼比。阻尼矩阵相关讨论参见: 「Python与地震工程」多自由度体系的阻尼矩阵
| 模态 | 自振圆频率 | 模态阻尼比 (直接构建阻尼矩阵) | 模态阻尼比 (瑞利阻尼,1、2阶模态) | 模态阻尼比 (瑞利阻尼,1、3阶模态) | 模态阻尼比 (瑞利阻尼,2、3阶模态) |
|---|---|---|---|---|---|
| 1 | 17.801675 | 0.0500 | 0.0500 | 0.0500 | 0.0901 |
| 2 | 49.879184 | 0.0500 | 0.0500 | 0.0420 | 0.0500 |
| 3 | 72.077509 | 0.0500 | 0.0623 | 0.0500 | 0.0500 |
瑞利阻尼只能确保所选用两阶模态对应阻尼比为预定值。
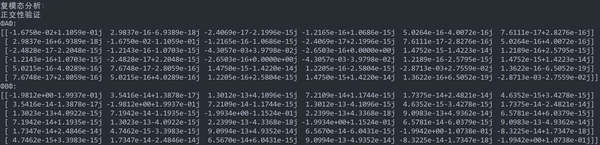
非对角线元素均为接近0的极小值,验证了模态的正交性。
转载本文请注明出处。科研成果中使用本文代码请引用作者课题组的研究论文:
本文使用 Zhihu On VSCode 创作并发布