温故知新——梯度下降(Gradient Descent)
梯度下降(Gradient Descent)又称最速下降,是迭代法的一种,可以用于求解最小二乘法(线性和非线性都可以)。在求解机器学习算法的模型参数,即无约束优化问题时,梯度下降(Gradient Descent)是最常采用的方法之一。在求解损失函数的最小值时,可以通过梯度下降法来一步步的迭代求解,得到最小化的损失函数和模型参数值。反过来,如果我们需要求解损失函数的最大值,这时就需要用梯度上升法来迭代了。
梯度下降的本质:是一种使用梯度去迭代更新权重参数使目标函数最小化的方法。
一、梯度下降的直观解释(最为经典的"下山"例子)
假设我们在一座大山上的某处位置(起点),由于我们不知道怎么下山,于是决定走一步算一步。在每走到一个位置的时候,求解当前位置的梯度,沿着梯度的负方向,也就是当前最陡峭的位置向下走一步。然后继续求解当前位置梯度,向这一步所在位置沿着最陡峭最易下山的位置走一步。这样一步步的走下去,一直走到觉得我们已经到了山脚。当然这样走下去,有可能我们不能走到山脚,而是到了某一个局部的山峰低处。


从上面可以看出,梯度下降不一定能够找到全局的最优解,有可能是一个局部最优解。当然,如果损失函数是凸函数,梯度下降法得到的解就一定是全局最优解。这里给出一个关于局部最小值和全局最小值的直观的理解。

除了局部极小值,还有一类值为“鞍点”,简单来说,它就是在某一些方向梯度下降,另一些方向梯度上升,形状似马鞍,如下图红点就是鞍点。

对于深度学习模型的优化来说,鞍点比局部极大值点或者极小值点带来的问题更加严重。
很多机器学习或深度学习模型都以凸函数(convex function)作为损失函数,到底什么是凸函数呢?下面简单介绍一下凸函数。
凸函数的定义:如果函数f(x)在某段区间上的任意两个点 x_{1},x_{2},都有f(tx_{1} + (1-t)x_{2}) \le tf(x_{1}) + (1-t)f(x_{2}),则称其在某段区间上凸函数。

凸函数其实就是在某段区间只有一个低谷的函数。下图二维的例子会更加直观地理解,"碗状"曲线,"碗口"向上。

二、梯度下降算法的过程
我们以线性回归为例: h_{\theta}(x)=\theta_{0}+\theta_{1}x 。假设我们一共有 m 个样本, (x^{(i)},y^{(i)}) (i=1,2,...,m) 。则损失函数为:
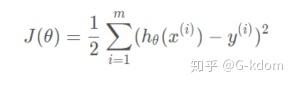
其中 \theta 可以看做是一个参数向量, (\theta_{0},\theta_{1})^{T} 。
计算损失函数的梯度,可以得到:

也就是说,为了使损失函数达到局部最小值,我们只需要沿着这个向量的反方向进行迭代即可。
那么参数的值到底该一次变化多少呢?我们通常用 \alpha 来表示这个大小,称为“步长”。它的值是需要我们手动设定的。显然,步长太小,迭代速度太慢,很长时间算法都不能结束;而步长太大,会导致迭代过快,则有可能在下降时跳过了最优解。所以,我们应该根据实际的情况,合理地设置 \alpha 的值。
在每次迭代中,我们令

即可使损失函数最终收敛到全局最小值或局部最小值,我们也得到了我们想要的参数值。
下图是在平面上的梯度下法示意图。从图中我们可以看出,每一次迭代是沿该点梯度的负方向进行的,一步一步趋向于局部最小值或全局最小值的。
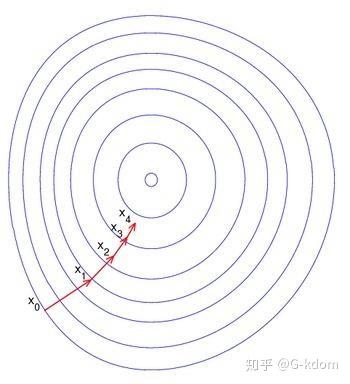
对梯度下降算法的过程进行一下总结:
1. 确认优化模型的假设函数和损失函数;
2. 参数初始化:主要是初始化 \theta_{i} (i=0,1,...,n) ,算法终止距离 \varepsilon 以及步长 \alpha ;
3. 确定当前位置的损失函数的梯度;
4. 用步长乘以损失函数的梯度,得到当前位置下降的距离;
5. 更新所有的 \theta_{i} ;
6. 确定是否所有的 \theta_{i} 梯度下降的距离都小于 \varepsilon 。如果小于 \varepsilon 则算法终止,当前所有的 \theta_{i} 即为最终结果。否则进入步骤5,继续更新。
三、梯度下降法的缺点:
1. 不能保证收敛到全局最优解
2. 靠近极小值时收敛速度减慢。
3. 直线搜索时可能会产生一些问题。
4. 可能会出现“之字形”下降。
