David Silver 增强学习——Lecture 5 不基于模型的控制（三）

地平线机器人｜轨迹/行为预测｜（逆）强化学习｜运动规划

其他lecture

离策略学习 Off-Policy Learning \textrm{On-Policy Learning} 的特点就是当前遵循的策略就是个体学习改善的策略。 \textrm{Off-Policy Learning} 则指的是在遵循一个策略 \mu(a|s) 的同时评估另一个策略 \pi(a|s) ，也就是计算确定在 \pi(a|s) 策略下的状态价值函数 v_{\pi}(s) 或状态行为价值函数 q_{\pi}(s, a) 。 \textrm{Off-Policy Learning} 的优势在于：

可以从人类给出的示教样本或其他智能体给出的引导样本中学习；
可以重用由旧策略生成的经验；
可以在使用一个探索性策略的同时学习一个确定性策略；
可以用一个策略进行采样，然后同时学习多个策略。

重要性采样（Importance Sampling）

详情请参考：

离策略学习中的重要性采样

考虑 t 时刻之后的动作状态轨迹 \rho_t= A_t,S_{t+1}, A_{t+1},· · ·,S_T ，可以得到该轨迹出现的概率为 {\Bbb P}\left( \rho_t \right)=\prod_{k=t}^{T-1}\pi\left( A_k|S_k \right){\Bbb P}\left( S_{k+1}|S_k,A_k \right) 因此可以得到相应的重要性权重为 \eta_t^T=\frac{\prod_{k=t}^{T-1}\pi\left( A_k|S_k \right){\Bbb P}\left( S_{k+1}|S_k,A_k \right)}{\prod_{k=t}^{T-1}\mu\left( A_k|S_k \right){\Bbb P}\left( S_{k+1}|S_k,A_k \right)}=\prod_{k=t}^{T-1}\frac{\pi\left( A_k|S_k \right)}{\mu\left( A_k|S_k \right)} 即便是未知环境模型，也能得到重要性权重。

离策略蒙特卡洛学习中的重要性采样 Importance Sampling for Off-Policy Monte-Carlo

对于off-policy Monte-Carlo使用importance sampling：

使用面向Monte-Carlo的策略 \mu 产生的return来估计策略 \pi ；
G_t^{\pi / \mu}=\frac{\pi(A_t|S_t)}{\mu(A_{t}|S_{t})} \frac{\pi(A_{t+1}|S_{t+1})}{\mu(A_{t+1}|S_{t+1})} ... \frac{\pi(A_T|S_T)}{\mu(A_T|S_T)}G_t ；
更新价值： V(S_t)\leftarrow V(S_t)+\alpha (G_t^{\pi / \mu}-V(S_t)) 。

我们知道，MC方法的方差本来就很大，而重要性采样将会使得方差急剧增大，因此结合重要性采样的MC方法就很难用了。

离策略TD学习中的重要性采样 Importance Sampling for Off-Policy TD

离策略TD Learning的任务就是使用TD方法在遵循一个策略 \mu(a|s) 的同时评估另一个策略 \pi(a|s) 。具体数学表示为： V(S_t)\leftarrow V\left( S_t \right)+\alpha\left( \underline{\frac{\pi(A_t|S_t)}{\mu(A_t|S_t)}\left( R_{t+1}+\gamma V\left( S_{t+1} \right) \right)}-V\left( S_t \right) \right) 这个公式可以这样解释：个体处在状态 S_t 中，基于策略 \mu 产生了一个行为 A_t ，执行该行为后进入新的状态 S_{t+1} ，那么在当前策略下如何根据新状态的价值调整原来状态的价值呢？离策略的方法就是，在状态 S_t 时比较另一个策略 \pi 和当前策略 \mu 产生行为 A_t 的概率大小，如果策略 \pi 得到的概率值与当前策略 \mu 得到的概率值接近，说明根据状态 S_{t+1} 价值来更新 S_t 的价值同时得到两个策略的支持，这一更新操作比较有说服力。同时也说明在状态 S_t 时，两个策略有接近的概率选择行为 A_t 。假如这一概率比值很小，则表明如果依照被评估策略，选择 A_t 的机会很小，这时候我们在更新 S_t 价值的时候就不能过多的考虑基于当前策略得到的状态 S_{t+1} 的价值。同样概率比值大于 1 时的道理也类似。这就相当于借鉴被评估策略的经验来更新我们自己的策略。

\textrm{Q-learning}

应用上述思想最好的方法是基于 \textrm{TD(0)} 的 \textrm{Q-learning} 。在 \textrm{Q-learning} 的过程中， t 时刻与环境进行实际交互的行为 A_t 由策略 \mu 产生： A_t\sim\mu\left( \cdot|S_t \right) ，策略 \mu 是一个 \epsilon-{\textrm{greedy}} 策略； t+1 时刻用来更新 Q 值的行为 A^{'}_{t+1} 由下式产生： A^{'}_{t+1}\sim\pi\left( \cdot|S_{t+1} \right) ，其中策略 \pi 是一个完全贪婪策略。因此，重要性采样的因子 \frac{\pi}{\mu} 就分两种情况。对于某个状态 s ， \pi 策略选择动作 a 的概率要么是 1 ，要么是 0 。当为 1 时， \mu 选择该动作的概率也较大（因为 \epsilon 一般比较小），所以 \frac{\pi}{\mu}\approx1 ；当为 0 时， \frac{\pi}{\mu}=0 。 因此，虽然 \textrm{Q-learning} 是一种离策略算法，它却不需要重要性采样因子了，或者说，不需要引入重要性采样。 TD目标值由之前的 R_{t+1} + \gamma Q\left( S_{t+1}, A_{t+1} \right),A_{t+1} \sim \mu\left( \cdot,S_t \right) 变成了 R_{t+1} + \gamma Q\left( S_{t+1}, A^{'} \right),A^{'} \sim \pi\left( \cdot,S_t \right) 。（注： A_{t+1} 表示智能体在 t+1 真的执行了该动作， A^{'} 为一个变量，并没有被实际执行！）公式如下： Q\left( S_t, A_t \right) \leftarrow Q\left( S_t, A_t \right) + \alpha\left( \mathop{\underline{R_{t+1} + \gamma Q\left( S_{t+1}, A^{'} \right)}}_\textrm{TD目标} − Q\left( S_t, A_t \right) \right)

Q-Learning进行离策略控制

\textrm{Q-learning} 最主要的表现形式是：个体遵循的策略是基于当前状态行为价值函数 Q(s,a) 的一个 \epsilon-{\textrm{greedy}} 策略，而目标策略是基于当前状态行为价值函数 Q(s,a) 不包含 \epsilon 的完全贪婪策略： \pi\left( S_{t+1} \right)=\mathop{\textrm{argmax}}_{a^{'}}Q\left( S_{t+1},a^{'} \right) 。这样 \textrm{Q-learning} 的TD目标值可以被大幅简化： \begin{align*} R_{t+1} + \gamma Q\left( S_{t+1}, A^{'} \right)&= R_{t+1} + \gamma Q\left( S_{t+1}, \mathop{\textrm{argmax}}_{a^{'}}Q\left( S_{t+1},a^{'} \right) \right)\\&= R_{t+1} + \max_{a^{'}}\gamma Q\left( S_{t+1}, a^{'} \right) \end{align*} 根据这种价值更新的方式，状态 S_t 依据 \epsilon-{\textrm{greedy}} 策略得到的行为 A_t 的价值将朝着 S_{t+1} 状态下完全贪婪策略确定的最大行为价值的方向做一定比例的更新。这种算法能够使个体的行为策略 \mu 更加接近完全贪婪策略，同时保证个体能持续探索并经历足够丰富的新状态。并最终收敛至最优策略和最优行为价值函数。

Q-Learning控制算法

定理： \textrm{Q-learning} 控制将收敛至最优状态行为价值函数： Q(s,a) \rightarrow q_*(s,a) 。

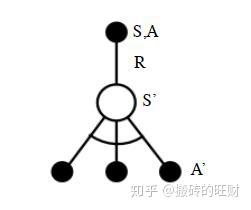
首先我们基于状态 S ，用 \epsilon-{\textrm{greedy}} 法选择到动作 A ，然后执行动作 A ，得到奖励 R ，并进入状态 S^{'} ，此时，如果是 \textrm{SARSA} ，会继续基于状态 S^{'} ，用 \epsilon-{\textrm{greedy}} 法选择 A^{'} ，然后更新价值函数。但是 \textrm{Q-learning} 则不同。对于 \textrm{Q-learning} ，它基于状态 S^{'} ，没有使用 \epsilon-{\textrm{greedy}} 法选择 A^{'} ，而是使用贪婪法选择 A^{'} ，也就是说，选择使 Q\left( S^{'},a \right) 最大的 a 作为 A^{'} 来更新价值函数。用数学公式表示就是： Q\left( S,A \right) = Q\left( S,A \right) + \alpha\left( R+\gamma \max_aQ\left( S^{'},a \right) - Q\left( S,A \right) \right) 对应到上图中就是在图下方的三个黑圆圈动作中选择一个使 Q\left( S^{'},a \right) 最大的动作作为 A^{'} 。此时选择的动作只会参与价值函数的更新，不会真正的执行。价值函数更新后，新的执行动作需要基于状态 S^{'} ，用 \epsilon-{\textrm{greedy}} 法重新选择得到。这一点也和 \textrm{SARSA} 稍有不同。对于 \textrm{SARSA} ，价值函数更新使用的 A^{'} 会作为下一阶段开始时候的执行动作。

Q-Learning算法进行离策略控制

下面我们总结下 \textrm{Q-learning} 算法的流程。算法输入：迭代轮数 T ，状态集 S ，动作集 A ，步长 \alpha ，衰减因子 \gamma ，探索率 \epsilon ；算法输出：所有的状态和动作对应的价值 Q 。 1. 随机初始化所有的状态和动作对应的价值 Q ；对于终止状态其 Q 值初始化为0。 2. \textrm{for i from 1 to T} ，进行迭代。 a) 初始化 S 为当前状态序列的第一个状态。 b) 用 \epsilon-{\textrm{greedy}} 在当前状态 S 选择出动作 A c) 在状态 S 执行当前动作 A ，得到新状态 S^{'} 和奖励 R d) 更新价值函数 Q\left( S,A \right) ： Q(S,A) + \alpha(R+\gamma \max_aQ(S',a) - Q(S,A)) e) S=S' f) 如果 S^{'} 是终止状态，当前轮迭代完毕，否则转到步骤b)

Q-Learning算法实例：Windy GridWorld

import numpy as np import matplotlib matplotlib.use('Agg') import matplotlib.pyplot as plt # world height WORLD_HEIGHT = 7 # world width WORLD_WIDTH = 10 # wind strength for each column WIND = [0, 0, 0, 1, 1, 1, 2, 2, 1, 0] # possible actions ACTION_UP = 0 ACTION_DOWN = 1 ACTION_LEFT = 2 ACTION_RIGHT = 3 # probability for exploration EPSILON = 0.1 # Sarsa step size ALPHA = 0.5 # reward for each step REWARD = -1.0 START = [3, 0] GOAL = [3, 7] ACTIONS = [ACTION_UP, ACTION_DOWN, ACTION_LEFT, ACTION_RIGHT] def step(state, action): i, j = state if action == ACTION_UP: return [max(i - 1 - WIND[j], 0), j] elif action == ACTION_DOWN: return [max(min(i + 1 - WIND[j], WORLD_HEIGHT - 1), 0), j] elif action == ACTION_LEFT: return [max(i - WIND[j], 0), max(j - 1, 0)] elif action == ACTION_RIGHT: return [max(i - WIND[j], 0), min(j + 1, WORLD_WIDTH - 1)] else: assert False # play for an episode def episode(q_value): # track the total time steps in this episode time = 0 # initialize state state = START while state != GOAL: # choose an action based on epsilon-greedy algorithm if np.random.binomial(1, EPSILON) == 1: action = np.random.choice(ACTIONS) else: values_ = q_value[state[0], state[1], :] action = np.random.choice([action_ for action_, value_ in enumerate(values_) if value_ == np.max(values_)]) # keep going until get to the goal state next_state = step(state, action) #if np.random.binomial(1, EPSILON) == 1: # next_action = np.random.choice(ACTIONS) #else: values_ = q_value[next_state[0], next_state[1], :] next_action = np.random.choice([action_ for action_, value_ in enumerate(values_) if value_ == np.max(values_)]) # Sarsa update q_value[state[0], state[1], action] += \ ALPHA * (REWARD + q_value[next_state[0], next_state[1], next_action] - q_value[state[0], state[1], action]) state = next_state #action = next_action time += 1 return time def q_learning(): q_value = np.zeros((WORLD_HEIGHT, WORLD_WIDTH, 4)) episode_limit = 500 steps = [] ep = 0 while ep < episode_limit: steps.append(episode(q_value)) # time = episode(q_value) # episodes.extend([ep] * time) ep += 1 steps = np.add.accumulate(steps) plt.plot(steps, np.arange(1, len(steps) + 1)) plt.xlabel('Time steps') plt.ylabel('Episodes') plt.savefig('./q-learning.png') plt.close() # display the optimal policy optimal_policy = [] for i in range(0, WORLD_HEIGHT): optimal_policy.append([]) for j in range(0, WORLD_WIDTH): if [i, j] == GOAL: optimal_policy[-1].append('G') continue bestAction = np.argmax(q_value[i, j, :]) if bestAction == ACTION_UP: optimal_policy[-1].append('U') elif bestAction == ACTION_DOWN: optimal_policy[-1].append('D') elif bestAction == ACTION_LEFT: optimal_policy[-1].append('L') elif bestAction == ACTION_RIGHT: optimal_policy[-1].append('R') print('Optimal policy is:') for row in optimal_policy: print(row) print('Wind strength for each column:\n{}'.format([str(w) for w in WIND])) if __name__ == '__main__': q_learning() 绝大部分代码和 \textrm{SARSA} 是类似的。这里我们可以重点比较和 \textrm{SARSA} 不同的部分。区别都在episode这个函数里面。首先是初始化的时候，我们只初始化状态 S ，把 A 的产生放到了while循环里面，而回忆下 \textrm{SARSA} 会同时初始化状态 S 和动作 A ，再去执行循环。下面这段 \textrm{Q-learning} 的代码对应算法的第二步步骤a和b： # play for an episode def episode(q_value): # track the total time steps in this episode time = 0 # initialize state state = START while state != GOAL: # choose an action based on epsilon-greedy algorithm if np.random.binomial(1, EPSILON) == 1: action = np.random.choice(ACTIONS) else: values_ = q_value[state[0], state[1], :] action = np.random.choice([action_ for action_, value_ in enumerate(values_) if value_ == np.max(values_)]) 接着我们会去执行动作 A ，得到 S^{'} ，由于奖励不是终止就是 -1 ，不需要单独计算。这部分和 \textrm{SARSA} 的代码相同。对应我们 \textrm{Q-learning} 算法的第二步步骤c： next_state = step(state, action) def step(state, action): i, j = state if action == ACTION_UP: return [max(i - 1 - WIND[j], 0), j] elif action == ACTION_DOWN: return [max(min(i + 1 - WIND[j], WORLD_HEIGHT - 1), 0), j] elif action == ACTION_LEFT: return [max(i - WIND[j], 0), max(j - 1, 0)] elif action == ACTION_RIGHT: return [max(i - WIND[j], 0), min(j + 1, WORLD_WIDTH - 1)] else: assert False 后面我们用贪婪法选择出最大的 Q\left( S^{'},a \right) ，并更新价值函数，最后更新当前状态 S 。对应我们 \textrm{Q-learning} 算法的第二步步骤d、e。注意 \textrm{SARSA} 这里是使用 \epsilon-{\textrm{greedy}} 法，而不是贪婪法。同时 \textrm{SARSA} 会同时更新状态 S 和动作 A ，而 \textrm{Q-learning} 只会更新当前状态 S 。 values_ = q_value[next_state[0], next_state[1], :] next_action = np.random.choice([action_ for action_, value_ in enumerate(values_) if value_ == np.max(values_)]) # Sarsa update q_value[state[0], state[1], action] += \ ALPHA * (REWARD + q_value[next_state[0], next_state[1], next_action] - q_value[state[0], state[1], action]) state = next_state

示例——悬崖行走（Cliff Walking Example ）

图中悬崖用灰色的长方形表示，在其两端一个是起点，一个是目标终点。途中从悬崖指向起点的箭头提示悬崖同时也是终止状态。可以看出最优路线是贴着悬崖上方行走。

早期 \textrm{Q-learning} 得到的策略要比 \textrm{SARSA} 要差一些，但后期总能找到最优策略。两者的曲线都有一定的起伏，说明两者都有一定的探索，即遵循的策略都是 \epsilon-{\textrm{greedy}} 执行的，但 \textrm{Q-learning} 在进行价值评估时采用的是 {\textrm{greedy}} 而不是再是 \epsilon-{\textrm{greedy}} 方法确定要观察的状态 S^{'} 。

一个Q-learning算法的简明教程

假设一幢建筑里面有5个房间（如上图所示），房间之间通过门相连。我们将这5个房间按照0、1、2、3、4进行编号，且建筑的外围可认为是一个大的房间，编号为5。上图的房间也可通过一个图来表示，房间作为图的节点，两个房间若有门相连，则相应节点间对应一条边，如下图所示。

对于这个例子，我们首先将agent置于建筑中的任意一个房间，然后从那个房间开始，让其走到建筑外，那是我们的目标房间（即编号为5的房间）。为了将编号为5的房间设置为目标，我们为每一扇门（即相应的边）关联一个reward值：直接连接到目标房间的门的reward值为100，其他门的reward值为0。因为每一扇门都有两个方向（如由0号房间可以去4号房间，而由4号房间也可以返回0号房间），因此每一个房间上指定两个箭头（一个指进一个指出），且每个箭头上带有一个reward值。注意，编号为5的房间有一个指向自己的箭头，其reward值为100，其他直接指向目标房间的边的reward值也为100。 \textrm{Q-learning} 的目标是达到reward值最大的state，因此，当agent到达目标房间后将永远停留在那里。这种目标也称为“吸收目标”。想象一下，我们的agent是一个可以通过经验进行学习的“哑巴虚拟机器人”，它可以从一个房间走到另一个房间，但是，它不知道周边的环境，也不知道怎样走到建筑的外面去。下面我们想对agent从建筑里的任意房间的简单撤离进行建模。假定现在agent位于2号房间，我们希望agent通过学习到达5号房间。我们将每个房间（包括5号房间）称为一个“状态”，将agent从一个房间走到另外一个房间称为一个“行为”。在上图中，一个“状态”对应一个节点，而一种“行为”对应一个箭头。假设agent当前处于状态2。从状态2，它可以转至状态3（因为状态2到状态3有边相连）。但从状态2不能转至状态1（因为状态2到状态1没边相连）。类似地，我们还有：从状态3，它可以转至状态1和4，也可以转回至状态2；从状态4，它可以转至状态0，5和3；从状态1，它可以转至状态5和3；从状态0，它只能转至状态4。我们可以以状态为行，行为为列，构建一个如下图所示的关于reward值的矩阵 R ，其中的 -1 表示空值（相应节点之间没有边相连）。

类似地，我们也可以构建一个矩阵 Q ，它用来表示agent已经从经验中学到的知识。矩阵 Q 与 R 是同阶的，其行表示状态，列表示行为。由于刚开始时agent对外界环境一无所知，因此矩阵 Q 应初始化为零矩阵。

为简单起见，在本例中我们假设状态的数目是已知的（等于 6）。对于状态数目未知的情形，我们可以让 Q 从一个元素出发，每次发现一个新的状态时就可以在 Q 中增加相应的行列。 \textrm{Q-learning} 算法的转移规则比较简单，如下式所示： Q\left( s,a \right) = R\left( s,a \right)+ \mathop{\underline{\gamma}}_{=0.8} \cdot \max_{\widetilde a}Q\left( \widetilde s,\widetilde a \right) 。观察矩阵 R 的第二行（对应房间1或状态1），它包含两个非负值，即当前状态1的下一步行为有两种可能：转至状态3或转至状态5。随机地，我们选取转至状态5。

想象一下，当我们的agent位于状态5以后，会发生什么事情呢？观察矩阵 R 的第6行（对应状态5），它对应三个可能的行为：转至状态1、4或5。根据公式 Q\left( s,a \right) = R\left( s,a \right)+\gamma\cdot \max_{\widetilde a}Q\left( \widetilde s,\widetilde a \right) ，我们有： \begin{align*} Q \left( 1,5 \right) &= R \left( 1,5 \right)+0.8\ast\max\left\{ Q\left( 5,1 \right) , Q \left( 5,4 \right), Q \left( 5,5 \right) \right\}\\ &=100+ 0.8 * \max\left\{ 0,0,0 \right\}\\ &=100 \end{align*}

现在状态5变成了当前状态。因为状态5即为目标状态，故一次episode便完成了，至此，agent的“大脑”中的 Q 矩阵刷新为：

接下来，进行下一次episode的迭代，首先随机地选取一个初始状态，这次我们选取状态3作为初始状态。观察矩阵 R 的第四行（对应状态3），它对应三个可能的行为：转至状态1、2或4。随机地，我们选取转至状态1。因此观察矩阵 R 的第二行（对应状态1），它对应两个可能的行为：转至状态3或5。根据公式 Q\left( s,a \right) = R\left( s,a \right)+\gamma\cdot \max_{\widetilde a}Q\left( \widetilde s,\widetilde a \right) ，我们有： \begin{align*} Q \left( 3,1 \right) &= R \left( 3,1 \right)+0.8\ast\max\left\{ Q\left( 1,3 \right) , Q \left( 1,5 \right)\right\}\\ &=0+ 0.8 * \max\left\{ 0,100 \right\}\\ &=80 \end{align*}

注意上式中的 Q \left( 1,5 \right) 用到了上图中的刷新值。此时，矩阵 Q 变为：

现在状态1变成了当前状态。因为状态1还不是目标状态，因此我们需要继续往前探索。状态1对应两个可能的行为：转至状态3或5。不妨假定我们幸运地选择了状态5。此时，同前面的分析一样，状态5有三个可能的行为：转至状态1、4或5。根据公式 Q\left( s,a \right) = R\left( s,a \right)+\gamma\cdot \max_{\widetilde a}Q\left( \widetilde s,\widetilde a \right) ，我们有： \begin{align*} Q \left( 1,5 \right) &= R \left( 1,5 \right)+0.8\ast\max\left\{ Q\left( 5,1 \right) , Q \left( 5,4 \right),Q \left( 5,5 \right)\right\}\\ &=100+ 0.8 * \max\left\{ 0,0,0 \right\}\\ &=100 \end{align*}

注意，经过上一步刷新，矩阵 Q 并没有发生变化。因为状态5即为目标状态，故这一次episode便完成了，至此，agent的“大脑”中的 Q 矩阵刷新为

若我们继续执行更多的episode，矩阵 Q 将最终收敛成：

对其进行规范化，每个非零元素都除以矩阵 Q 的最大元素（这里为500），可得（这里省略了百分号）

一旦矩阵 Q 足够接近于收敛状态，我们的agent便学习到了转移至目标状态的最佳路径（如下图所示）。

SARSA vs Q-Learning

\textrm{Q-learning} 直接学习的是最优策略，而 \textrm{SARSA} 在学习最优策略的同时还在做探索。这导致我们在学习最优策略的时候，如果用 \textrm{SARSA} ，为了保证收敛，需要制定一个策略，使 \epsilon-{\textrm{greedy}} 法的超参数 \epsilon 在迭代的过程中逐渐变小。 \textrm{Q-learning} 没有这个烦恼。另外一个就是 \textrm{Q-learning} 直接学习最优策略，但是最优策略会依赖于训练中产生的一系列数据，所以受样本数据的影响较大，因此受到训练数据方差的影响很大，甚至会影响 Q 函数的收敛。 \textrm{Q-learning} 的深度强化学习版 \textrm{Deep Q-Learning} 也有这个问题。在学习过程中， \textrm{SARSA} 在收敛的过程中鼓励探索，这样学习过程会比较平滑，不至于过于激进，导致出现像 \textrm{Q-learning} 可能遇到一些特殊的最优“陷阱”。在实际应用中，如果我们是在模拟环境中训练强化学习模型，推荐使用 \textrm{Q-learning} ，如果是在线生产环境中训练模型，则推荐使用 \textrm{SARSA} 。

总结DP与TD关系

下面两张图概括了各种DP算法和各种TD算法，同时也揭示了各种不同算法之间的区别和联系。总的来说TD是采样+有数据引导（bootstrap），DP是全宽度+实际数据。如果从Bellman期望方程角度看：聚焦于状态本身价值的是迭代法策略评估（DP）和TD学习，聚焦于状态行为对价值函数的则是Q-策略迭代（DP）和SARSA；如果从针对状态行为价值函数的Bellman优化方程角度看，则是Q-价值迭代（DP）和Q学习。