sympy: 符号运算-1
本文主要参考资料来自sympy的官网:
一般,我们使用计算机软件进行数学计算,主要是数值计算,就算有变量,也是代入具体数值来算的,我们在初中到大学学到的符号计算,很多时候无法用计算机来进行,比如下面的多项式化简:
y=ab+bc=b(a+c)
上面的式中没有任何一个具体数值,完全是符号进行计算,这时我们只能手算了。当然,我们可以用商业软件mathematics, 但是非常昂贵,幸好我们还有python,有了开源的sympy模块,我们可以做到如下功能:
- core symbolic mathematics: 基础运算,包括:化简Simplification,各种函数运算等;
- Polynomials:多项式运算及求解
- Calculus:极限、微分、积分
- Solving equations:各种方程求解
- Combinatorics:组合学
- Discrete math:离散数学
- Matrices:矩阵运算
- Geometry:几何学
- Physics:物理学
- Statistics:统计学
- Cryptography:密码学
下面我们分几个专题来介绍其功能,这篇介绍基础的运算。
- Symbols : 符号
在进行符号运算前,必须先定义符号,下面的例子我们定义了两个符号x,y:
import sympy as sy
x,y = sy.symbols('x y') #符号间用空格隔开
print(type(x))
print(type(y))输出:
sympy.core.symbol.Symbol
sympy.core.symbol.Symbol2. Symbols expression: 符号表达式
当一个表达式中有任何一个变量是sympy symbol,就变成一个symbols expression,它不会直接进行运算,除非你使用subs()方法代入具体的数值,看下面的例子:
import sympy as sy
x,y=sy.symbols("x y")
f=x**2+3*x-5
print(f"f(x)={f}") #直接打印f是显示表达式
xx=3
print(f"f({xx})={f.subs({x:xx})}") #代入具体数值来计算最终的结果
yy=4
f1=(x**2+y**2)**0.5
print(f"f1(x,y)={f1}") #直接打印f1是显示表达式
print(f"f1({xx},{yy})={f1.subs({x:xx, y:yy})}") #代入具体数值来计算最终的结果结果:
f(x)=x**2 + 3*x - 5
f(3)=13
f1(x,y)=(x**2 + y**2)**0.5
f1(3,4)=5.000000000000003. Substitution : 代换
上面的例子,显示了如何在表达式中代入具体的数值,但是替换还可以有更多的可能,看下面的例子:
f(x)=cos(x) , x(t)=a^t ---> f(t)=cos(a^t)
import sympy as sy
a,x,t=sy.symbols("a x t")
f=sy.cos(x)
print(f"f(t)={f.subs({x: a**t})}")输出:
f(t)=cos(a**t)4. evalf:计算出具体的值
不单单用sympy symbols组成的表达式,用sympy functions或sympy Rational组成的表达式,都是不会直接计算出实际的数值,这时候可以用evalf函数来实际计算出具体的数值,看下例:
import sympy as sy
y = sy.sqrt(2)+sy.Rational(3,8)
print(f"{y}={y.evalf()}")输出:
3/8 + sqrt(2)=1.789213562373105. 更漂亮和专业的输出
在ipython中,运行:sympy.init_printing()后,可以以比较漂亮的格式来打印(用sympy.pprint()函数)输出公式,比如:
import sympy as sy
sy.init_printing()
sy.pprint(x**2+sy.Rational(1,3)) 输出:
2 1
x + ─
3如果在jupyter notebook中,可以用下面的方法用latex来输出漂亮的公式:
from IPython.display import display, Latex
import sympy as sy
sy.init_printing()
x,y=sy.symbols("x y")
f=x**2+3*x-5
display(Latex(f"$$f(x)={sy.latex(f)}$$"))
xx=3
sy.pprint(f"f({xx})={f.subs({x:xx})}")
yy=4
f1=sy.sqrt(x**2+y**2)
display(Latex(f"$$f_1(x,y)={sy.latex(f1)}$$"))
sy.pprint(f"f1({xx},{yy})={f1.subs({x:xx, y:yy})}")输出:

关于latex的介绍,参见我的另一个专栏。
6. Simplification : 化简
对于sympy来说,最强大的一点就是对公式进行化简,下面显示几个例子:
from IPython.display import display, Latex
import sympy as sy
sy.init_printing()
x = sy.symbols("x")
y = (x**3 + x**2 - x - 1)/(x**2 + 2*x + 1)
display(Latex(f"$${sy.latex(y)}={sy.latex(sy.simplify(y))}$$"))输出:
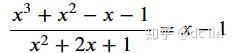
这里是用simplify()函数,绝大部分情况下它很好用,就是有几个问题:
- 它不能控制我们最终想要的形式,比如想要多项式(和式a+b+c)的最简式,还是多项乘积(a*b*c)的最简式,这可以用后面介绍的两个函数来取代;
- 它速度比较慢,同样,可以用其他更快的函数取代,但是通用性没有它好。
当我们需要化简为和式的表达式时,可以用expand()函数,参见下例:
from IPython.display import display, Latex
import sympy as sy
sy.init_printing()
x = sy.symbols("x")
y = (x + 1)**2
display(Latex(f"$${sy.latex(y)}={sy.latex(sy.expand(y))}$$")) 输出:
(x+1)^2=x^2+2x+1
当我们需要化简为乘积表达式时,可以用factor()函数,参见下例:
from IPython.display import display, Latex
import sympy as sy
sy.init_printing()
x = sy.symbols("x")
y = x**3 - x**2 + x - 1
display(Latex(f"$${sy.latex(y)}={sy.latex(sy.factor(y))}$$"))输出:
x^{3} - x^{2} + x - 1 =\left(x - 1\right) \left(x^{2} + 1\right)
当我们的表达式各项有相同的变量,我们可以用collect()函数来合并同阶的项,看下例:
from IPython.display import display, Latex
import sympy as sy
sy.init_printing()
x,y,z = sy.symbols("x y z")
f = x*y + x - 3 + 2*x**2 - z*x**2 + x**3
display(Latex(f"$${sy.latex(f)}={sy.latex(sy.collect(f,x))}$$"))输出:
x^{3} - x^{2} z + 2 x^{2} + x y + x - 3 =x^{3} + x^{2} \left(- z + 2\right) + x \left(y + 1\right) - 3
当我们需要把表达式转换为 \frac{p}{q} 这样的最简式的时候,可以用cancel()函数,它会上下消除相同的项,见下例,另,cancel()函数最后分子分母都化简为多项式的和式,如果要化简为乘积式,可以用factor()函数。
from IPython.display import display, Latex
import sympy as sy
sy.init_printing()
x,y,z = sy.symbols("x y z")
f = (x*y**2 - 2*x*y*z + x*z**2 + y**2 - 2*y*z + z**2)/(x**2 - 1)
display(Latex(f"$${sy.latex(f)}={sy.latex(sy.cancel(f))}={sy.latex(sy.factor(f))}$$"))输出:
\frac{x y^{2} - 2 x y z + x z^{2} + y^{2} - 2 y z + z^{2}}{x^{2} - 1} =\frac{y^{2} - 2 y z + z^{2}}{x - 1}= \frac{\left(y - z\right)^{2}}{x - 1}
下面看看apart()函数,可以用来把分数表示的多项式因式分解,看例子:
from IPython.display import display, Latex
import sympy as sy
sy.init_printing()
x,y,z = sy.symbols("x y z")
f = (4*x**3 + 21*x**2 + 10*x + 12)/(x**4 + 5*x**3 + 5*x**2 + 4*x)
display(Latex(f"$${sy.latex(f)}={sy.latex(sy.apart(f))}$$"))
print(sy.latex(f), sy.latex(sy.apart(f)))输出:
\frac{4 x^{3} + 21 x^{2} + 10 x + 12}{x^{4} + 5 x^{3} + 5 x^{2} + 4 x} =\frac{2 x - 1}{x^{2} + x + 1} - \frac{1}{x + 4} + \frac{3}{x}
对于三角函数,可以用:trigsimp()函数来化简,比如下例:
from IPython.display import display, Latex
import sympy as sy
sy.init_printing()
x,y,z = sy.symbols("x y z")
f = sin(x)**4 - 2*cos(x)**2*sin(x)**2 + cos(x)**4
display(Latex(f"$${sy.latex(f)}={sy.latex(sy.trigsimp(f))}$$"))\sin^{4}{\left (x \right )} - 2 \sin^{2}{\left (x \right )} \cos^{2}{\left (x \right )} + \cos^{4}{\left (x \right )} =\frac{\cos{\left (4 x \right )}}{2} + \frac{1}{2}
反过来,可以用expand_trig()函数来展开三角函数,看下例:
from IPython.display import display, Latex
import sympy as sy
sy.init_printing()
x,y,z = sy.symbols("x y z")
f = sin(x+y)
display(Latex(f"$${sy.latex(f)}={sy.latex(sy.expand_trig(f))}$$"))输出:
\sin{\left (x + y \right )}= \sin{\left (x \right )} \cos{\left (y \right )} + \sin{\left (y \right )} \cos{\left (x \right )}
对于指数函数的化简,比较麻烦,因为一般指数函数的形式: x^a\cdot y^b ,对于底: x,y 和指数: a,b,当它们取不同类型的值或范围的时候,其结果是不一样的,比如:
- x^c \cdot y^c :当 x,y 都是正数,且 c 是实数,可以化简为: x^c\cdot y^c = (xy)^c ,但是 其他情况就不行,比如设 x=y=-1 , c=0.5 ,则 x^c\cdot y^c=\sqrt{-1}\cdot \sqrt{-1} = i\cdot i = -1 ,而 (x\cdot y)^c = \sqrt{-1\cdot -1}=1 ,两边不相等;
- (x^a)^b :当 b是整数时,可以化简为: (x^a)^b = x^{ab} ,但是其他情况下,就不行,比如:设: x=-1, a=2, b=0.5, (x^a)^b=\sqrt{(-1)^2}=1 , 而x^{ab}=(-1)^{2\cdot \frac{1}{2}}=-1 ,两者不相同;
- x^a\cdot x^b \equiv x^{a+b} :对于任何情况都合适。
缺省情况下,sympy假设symbols都是属于复数类型,这样上面的一些指数表达式就无法进行简化,而我们可以在定义symbols的时候,指定其属于什么类型,这样一些简化就可以进行,看下面的例子:
from IPython.display import display, Latex
import sympy as sy
sy.init_printing()
x, y = symbols('x y', positive=True) #定义为正实数
a, b = symbols('a b', real=True) #定义为实数
z, t, c = symbols('z t c')
f1 = t**c*z**c
f2 = x**a*x**b
f3 = x**a*y**a
display(Latex(f"$${sy.latex(f1)}={sy.latex(sy.powsimp(f1))}$$"))
display(Latex(f"$${sy.latex(f2)}={sy.latex(sy.powsimp(f2))}$$"))
display(Latex(f"$${sy.latex(f3)}={sy.latex(sy.powsimp(f3))}$$"))输出:
t^{c} z^{c} = t^{c} z^{c} \\ x^{a} x^{b} = x^{a + b} \\ x^{a} y^{a} =\left(x y\right)^{a}
注意上面第一个式子,由于 z,t,c 是复数,所以简化没法进行;
而第二、第三个式子中由于设定符号 x,y,a,b 都符合要求,所以可以进行简化。
除了这些以外,还有:expand_power_exp(), expand_power_base(), powdenest(), expand_log(), logcombine()等函数可以进行化简,参看下面的资料:

