Embedding的作用

要弄清楚embeding的作用，先要弄明白它和one hot encoding之间有什么的区别，embeding解决了什么one hot encoding不能解决的问题。

一、one hot encoding的概念

假设我们中文文章中，一共只有10个字。那么我们用0-9就可以表示完

比如，这10个字就是“我从哪里来，要到何处去”，其分别对应“0-9”，如下：

我 从 哪 里 来 要 到 何 处 去

0 1 2 3 4 5 6 7 8 9

那么，其实我们只用一个列表（一维）就能表示所有的对话

如：我 从 哪 里 来 要 到 何 处 去 ——>>>[0 1 2 3 4 5 6 7 8 9]

或：我 从 何 处 来 要 到 哪 里 去 ——>>>[0 1 7 8 4 5 6 2 3 9]

我们把上面的编码方式弄成one hot encoding

# 我从哪里来，要到何处去
[
[1 0 0 0 0 0 0 0 0 0]
[0 1 0 0 0 0 0 0 0 0]
[0 0 1 0 0 0 0 0 0 0]
[0 0 0 1 0 0 0 0 0 0]
[0 0 0 0 1 0 0 0 0 0]
[0 0 0 0 0 1 0 0 0 0]
[0 0 0 0 0 0 1 0 0 0]
[0 0 0 0 0 0 0 1 0 0]
[0 0 0 0 0 0 0 0 1 0]
[0 0 0 0 0 0 0 0 0 1]
]

# 我从何处来，要到哪里去
[
[1 0 0 0 0 0 0 0 0 0]
[0 1 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 1 0 0]
[0 0 0 0 0 0 0 0 1 0]
[0 0 0 0 1 0 0 0 0 0]
[0 0 0 0 0 1 0 0 0 0]
[0 0 0 0 0 0 1 0 0 0]
[0 0 1 0 0 0 0 0 0 0]
[0 0 0 1 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 1]
]

把每一个汉字都对应成一个10维的，且有一个维度是1的数组/列表，其中每一个字都用唯一的对应的数组/列表对应。例如，“我”表示成[1 0 0 0 0 0 0 0 0 0]，“去”表示成[0 0 0 0 0 0 0 0 0 1]，这样就把文本中的10个汉字整合成一个稀疏矩阵（二维）。

那问题来了，稀疏矩阵（二维）和列表（是直接用“我 从 哪 里 来 要 到 何 处 去” ——>>>[0 1 2 3 4 5 6 7 8 9]）的表达方式）相比，有什么优势。

很明显，计算简单嘛，稀疏矩阵做矩阵计算的时候，只需要把1对应位置的数相乘求和就行，也许你心算都能算出来；而一维列表，你能很快算出来？何况这个列表还是一行，如果是100行、1000行和或1000列呢？

所以，one-hot编码的优势就体现出来了，计算方便快捷、表达能力强。然而，缺点也随着来了。

比如：中文大大小小简体繁体常用不常用的大约有10万字，然后一篇文章100W字，你要表示成100W X 10W的矩阵？？？

这是它最明显的缺点。过于稀疏时，过度占用资源。

比如：其实我们这篇文章，虽然100W字，但是其实我们整合起来，有99W字是重复的，只有1W字是完全不重复的。那我们用100W X 10W的岂不是白白浪费了99W X 10W的矩阵存储空间。

那怎么办？？？

这时，Embedding层横空出世。

二、Embeddin概念

接下来给大家看一张图

链接：词向量与Embedding究竟是怎么回事？ - 科学空间|Scientific Spaces

假设：我们有一个2 x 6的矩阵，然后乘上一个6 x 3的矩阵后，变成了一个2 x 3的矩阵。

先不管它什么意思，这个过程，我们把一个12个元素的矩阵变成6个元素的矩阵，直观上，大小是不是缩小了一半？

也许你已经想到了！！！对！！！不管你想的对不对，但是embedding层，在某种程度上，就是用来降维的，降维的原理就是矩阵乘法。在卷积网络中，可以理解为特殊全连接层操作，跟1x1卷积核异曲同工！！！

复习一下，矩阵乘法需要满足一个条件。
A X B时，B的行数必须等于A的列数
得出的结果为A的行数 X B的列数的一个矩阵

也就是说，假如我们有一个100W X10W的矩阵，用它乘上一个10W X 20的矩阵，我们可以把它降到100W X 20，瞬间量级降了。。。10W/20=5000倍！！！

这就是嵌入层的一个作用——降维。

然后中间那个10W X 20的矩阵，可以理解为查询表，也可以理解为映射表，也可以理解为过度表。

接着，既然可以降维，当然也可以升维。为什么要升维？

这也是很神奇的。咱们再举一个例子：

这张图，我要你在10米开外找出五处不同！。。烦请出题者走近两步，我先把我的刀拿出来，您再说一遍题目我没听清。

当然，目测这是不可能完成的。但是我让你在一米外，也许你一瞬间就发现衣服上有个心是不同的，然后再走近半米，你又发现左上角和右上角也是不同的。再走近20厘米，又发现耳朵也不同，最后，在距离屏幕10厘米的地方，终于发现第五个不同的地方在耳朵下面一点的云。

但是，其实无限靠近并不代表认知度就高了，比如，你只能距离屏幕1厘米远的地方找，找出五处不同。。。出题人你是不是脑袋被门挤了。。。

由此可见，距离的远近会影响我们的观察效果。同理也是一样的，低维的数据可能包含的特征是非常笼统的，我们需要不停地拉近拉远来改变我们的感受野，让我们对这幅图有不同的观察点，找出我们要的茬。

embedding的又一个作用体现了。对低维的数据进行升维时，可能把一些其他特征给放大了，或者把笼统的特征给分开了。同时，这个embedding是一直在学习在优化的，就使得整个拉近拉远的过程慢慢形成一个良好的观察点。比如：我来回靠近和远离屏幕，发现45厘米是最佳观测点，这个距离能10秒就把5个不同点找出来了。

回想一下为什么CNN层数越深准确率越高，卷积层卷了又卷，池化层池了又升，升了又降，全连接层连了又连。因为我们也不知道它什么时候突然就学到了某个有用特征。但是不管怎样，学习都是好事，所以让机器多卷一卷，多连一连，反正错了多少我会用交叉熵告诉你，怎么做才是对的我会用梯度下降算法告诉你，只要给你时间，你迟早会学懂。因此，理论上，只要层数深，只要参数足够，NN能拟合任何特征。

总之，它类似于虚拟出一个关系对当前数据进行映射。这个东西也许一言难尽吧，但是目前各位只需要知道它有这些功能的就行了。

想具体理解其作用，建议大家去探究探究卷积神经网络的各种中间过程，以及反向传播理论。到时候大家再来深入理解嵌入层时，那就一通百通了。

三、Word Embedding--介绍

1）单词表达

先前的卷积神经网络的一节中，提到过图片是如何在计算机中被表达的。 同样的，单词也需要用计算机可以理解的方式表达后，才可以进行接下来的操作。

1.1）One hot representation

程序中编码单词的一个方法是one hot encoding。

实例：有1000个词汇量。排在第一个位置的代表英语中的冠词"a"，那么这个"a"是用[1,0,0,0,0,...]，只有第一个位置是1，其余位置都是0的1000维度的向量表示，如下图中的第一列所示。

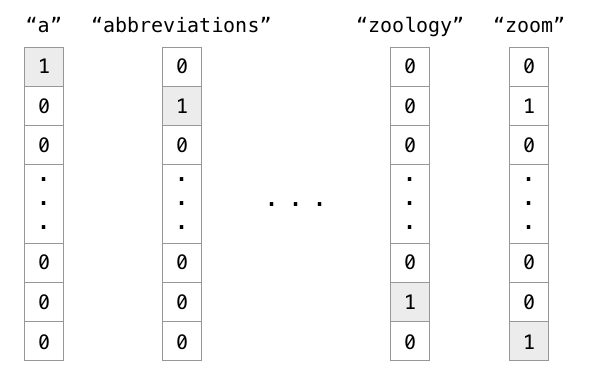
也就是说，

在one hot representation编码的每个单词都是一个维度，彼此independent。

1.2）Distributed representation

然而每个单词彼此无关这个特点明显不符合我们的现实情况。我们知道大量的单词都是有关。

语义：girl和woman虽然用在不同年龄上，但指的都是女性。

复数：word和words仅仅是复数和单数的差别。

时态：buy和bought表达的都是“买”，但发生的时间不同。

所以用one hot representation的编码方式，上面的特性都没有被考虑到。

我们更希望用诸如“语义”，“复数”，“时态”等维度去描述一个单词。每一个维度不再是0或1，而是连续的实数，表示不同的程度。

1.3）目的

但是说到底，为什么我们想要用Distributed representation的方式去表达一个单词呢? 这样做带来了什么好处？

1.4）数据量角度

这需要再次记住我们的目的：

机器学习：从大量的个样本 {\{(x_i,y_i)^N_{i=1}}\} 中，寻找可以较好预测未见过 x_{new} 所对应 y_{new} 的函数 f:x\rightarrow y 。

实例：在我们日常生活的学习中，大量的 {\{(x_i,y_i)^N_{i=1}}\} 就是历年真题， x_i 是题目，而 y_i 是对应的正确答案。高考时将会遇到的 x_{new} 往往是我们没见过的题目，希望可以通过做题训练出来的解题方法 f:x\rightarrow y 来求解出正确的 y_{new} 。

如果可以见到所有的情况，那么只需要记住所有的 x_i 所对应的 y_i 就可以完美预测。但正如高考无法见到所有类型的题一样，我们无法见到所有的情况。这意味着，

机器学习需要从有限的例子中寻找到合理的 f 。

高考有两个方向提高分数：

• 方向一：训练更多的数据：题海战术。
• 方向二：加入先验知识：尽可能排除不必要的可能性。

问题的关键在于训练所需要的数据量上。

同理，如果我们用One hot representation去学习，那么每一个单词我们都需要实例数据去训练，即便我们知道"Cat"和"Kitty"很多情况下可以被理解成一个意思。

2）神经网络分析

假设我们的词汇只有4个，girl, woman, boy, man，下面就思考用两种不同的表达方式会有什么区别。

2.1）One hot representation

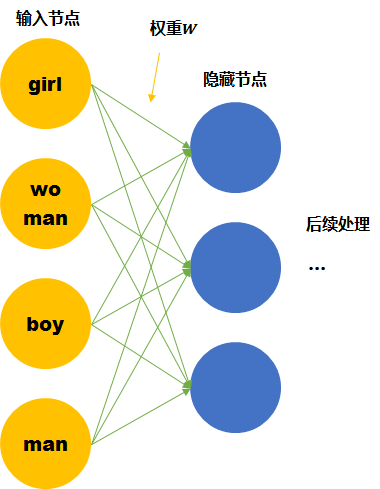
尽管我们知道他们彼此的关系，但是计算机并不知道。在神经网络的输入层中，每个单词都会被看作一个节点。 而我们知道训练神经网络就是要学习每个连接线的权重。如果只看第一层的权重，下面的情况需要确定4*3个连接线的关系，因为每个维度都彼此独立，girl的数据不会对其他单词的训练产生任何帮助，训练所需要的数据量，基本就固定在那里了。

2.2)Distributed representation

我们这里手动的寻找这四个单词之间的关系 f 。可以用两个节点去表示四个单词。每个节点取不同值时的意义如下表。 那么girl就可以被编码成向量[0,1]，man可以被编码成[1,1]（第一个维度是gender，第二个维度是age）。

那么这时再来看神经网络需要学习的连接线的权重就缩小到了2*3。同时，当送入girl为输入的训练数据时，因为它是由两个节点编码的。那么与girl共享相同连接的其他输入例子也可以被训练到（如可以帮助到与其共享female的woman，和child的boy的训练）。

Word embedding也就是要达到第二个神经网络所表示的结果，降低训练所需要的数据量。

而上面的四个单词可以被拆成2个节点的是由我们人工提供的先验知识将原始的输入空间经过 f(上图中的黄色箭头)投射到了另一个空间（维度更小），所以才能够降低训练所需要的数据量。 但是我们没有办法一直人工提供，机器学习的宗旨就是让机器代替人力去发现pattern。

Word embedding就是要从数据中自动学习到输入空间到Distributed representation空间的 映射f 。

2.3)训练方法

问题来了，我们该如何自动寻找到类似上面的关系，将One hot representation转变成Distributed representation。 我们事先并不明确目标是什么，所以这是一个无监督学习任务。

无监督学习中常用思想是：当得到数据{\{(x_i,y_i)^N_{i=1}}\}后，我们又不知道目标（输出）时，

• 方向一：从各个输入 {{x_i}^N_{i=1} }之间的关系找目标。 如聚类。
• 方向二：并接上以目标输出 y_i 作为新输入的另一个任务 g:y \rightarrow z ，同时我们知道的对应 z_i值。用数据 {\{(x_i,z_i)^N_{i=1}}\} 训练得到 k:x \rightarrow z ,也就是 z=g(f(x)) ，中间的表达 y=f(x) 则是我们真正想要的目标。如生成对抗网络。

Word embedding更偏向于方向二。 同样是学习一个 k:x \rightarrow z ，但训练后并不使用 k ，而是只取前半部分的 f:x \rightarrow y 。

到这里，我们希望所寻找的 k:x \rightarrow z 既有标签 z ，又可以让 f(x) 所转换得到的 y 的表达具有Distributed representation中所演示的特点。

同时我们还知道，

单词意思需要放在特定的上下文中去理解。

那么具有相同上下文的单词，往往是有联系的。

实例：那这两个单词都狗的品种名，而上下文的内容已经暗指了该单词具有可爱，会舔人的特点。

• 这个可爱的 泰迪 舔了我的脸。
• 这个可爱的 金巴 舔了我的脸。

而从上面这个例子中我们就可以找到一个 k:x \rightarrow z ：预测上下文。

用输入单词 x 作为中心单词去预测其他单词 z 出现在其周边的可能性。

我们既知道对应的 z ，同时该任务 k 又可以让 f(x) 所转换得到的 y 的表达具有Distributed representation中所演示的特点。 因为我们让相似的单词（如泰迪和金巴）得到相同的输出（上下文），那么神经网络就会将泰迪的输入和金巴的输入经过神经网络 f(x) 得到的泰迪的输出和金巴的输出几乎相同。

用输入单词作为中心单词去预测周边单词的方式叫做：Word2Vec The Skip-Gram Model。

用输入单词作为周边单词去预测中心单词的方式叫做：Continuous Bag of Words (CBOW)。

参考:

原文链接：https://blog.csdn.net/weixin_42078618/article/details/82999906

原文链接：YJango：YJango的Word Embedding--介绍

“无意中发现了一个巨牛的人工智能教程，忍不住分享一下给大家。教程不仅是零基础，通俗易懂，而且非常风趣幽默，像看小说一样！觉得太牛了，所以分享给大家。点这里可以跳转到教程。