使用numpy来理解PCA和SVD
前言
线性代数是高等数学里面非常重要的一门课程,可惜在学校的时候是一种自底向上的学习方式,并不知道学出来有什么用,以致彻底沦为应试教育。后来在工作中接触了机器学习,才真正看到了“数学之美”,才发现线性代数是多么的优雅多么的有用。
今天我们来看看下线性代数中非常重要的一个知识点奇异值分解SVD Singular value decomposition。SVD在数据科学当中非常有用,其常见的应用包括: - 自然语言处理中的Latent Semantic Analysis - 推荐系统中的Collaborative Filtering - 降维常用套路Principal Component Analysis
LSA已经在前文中有所讲解,CF的话后面在推荐系统的专题中来写,今天主要聊聊PCA,以及SVD在PCA中的重要作用。同样延续我们“手撕”的传统,使用numpy来理解其中的原理。
PCA
Principal component analysis即主成分分析,是机器学习中一种非常常用的降维方式。其发源也是源自于早期的计算机处理能力有限,当数据样本的维度很高时,预先去除掉数据中的一些冗余信息和噪声(降维),使得数据变得更加简单高效,节省时间和成本。
在深度学习时代,更强调的是原始数据的直接输入,再通过神经网络来做降维工作,最典型是场景就是计算机视觉,直接输入原始图片像素信息,通过CNN卷积层、MaxPooling层来进行降维。因此PCA逐渐开始淡出人们的视线,通常是作为一种数据可视化的手段(二维图表无法展示多维的数据样本)。
其实,在深度学习目前尚未全面攻克的结构化数据领域,PCA仍然有较多的用,其数据处理的思路依然值得我们去学习揣摩。
PCA正常解法
PCA算法的本质,其实就是找到一些投影方向,使得数据在这些投影方向上的方差最大,且这些投影方向是相互正交的。找到新的正交基后,计算原始数据在这些正交基上投影的方差,方差越大,就说明对应正交基上包含了更多的信息量。
关于原始数据的方差,最好的一个工具就是协方差矩阵了。协方差矩阵的特征值越大,对应的方差也就越大,在对应的特征向量上投影的信息量就越大。因此,我们如果将小特征值对应方向的数据删除,就可以达到降维的目的。因此,在数学上,我们可以把问题转化为求原始数据的协方差矩阵,然后计算协方差矩阵的特征值与特征向量。
对于广大程序员来说,学习机器学习最重要的一个坎还是数学。很多实际的代码其实是公式推导后的结果的代码实现,如果没有理清公式推导的过程,那么最后肯定是一头雾水。所以,克服心中的恐惧,翻出压在箱底的《线性代数》,我们上。
首先,求原始数据X的协方差矩阵C,将原始矩阵中心化后,做如下操作
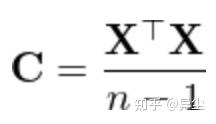
接着,由于协方差矩阵C是方阵,就可以通过特征分解的方式来求C的特征值和特征向量。

最后,选择最大的k个特征值进行保留,求X的k阶PCA(X右乘k阶特征向量)
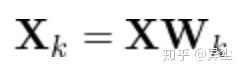
用SVD来解PCA
根据上面的推导,我们已经可以对矩阵X做PCA了。同学们可能要问了,这跟SVD有什么关系呢?
工程化思维强的同学应该已经想到了,这种纯数学的解法,在实际工程实践中有以下问题: - 在数据量很大时,把原始矩阵进行转置求协方差矩阵,然后再进行特征值分解是一个非常慢的过程。 - 稳定性问题。可以看到X转置乘以X,如果矩阵有非常小的数,很容易在平方中丢失。
工业界中,还是“唯快不破,唯稳不破”。我们知道,奇异值分解相对特征分解,有个很大的优势就是不要求原始矩阵是方阵。这非常符合现实生活中的数据。因此,有大神想到,是否可以用svd来解PCA?推导如下:
我们根据协方差矩阵的公式,把X按照奇异值分解展开,注意后面应用到了一个酋矩阵(unitary)的特性:

看到最后的结果,是否跟上面的

很像?没错。协方差矩阵C的特征值和X的奇异值有以下关系

而C的特征向量即为X的SVD分解后的V向量, 则参考PCA正常解法,X的k阶PCA即为_X右乘k阶V向量_。因此这种方式求PCA,只需要把原始矩阵做一次SVD分解即可,不用转置,不用求协方差矩阵。事实上,在Scikit Learn等机器学习框架中,就是用的SVD来做PCA。
用numpy来验证
numpy原始解法求PCA
接下来,我们用numpy来验证这种思路。首先是PCA的标准解法: 随机模拟一个原始数据矩阵,5个样本,3个特征:
import numpy as np
X = np.random.rand(5,3)
'''
array([[0.86568791, 0.73022945, 0.17982869],
[0.07201287, 0.99358411, 0.84389196],
[0.61267696, 0.08867997, 0.11770573],
[0.16898969, 0.3093472 , 0.9010064 ],
[0.43840269, 0.97250927, 0.64897872]])
'''将矩阵中心化,即减去均值:
X_new = X - np.mean(X, axis=0)
'''
array([[ 0.43413389, 0.11135945, -0.35845361],
[-0.35954115, 0.37471411, 0.30560966],
[ 0.18112294, -0.53019003, -0.42057657],
[-0.26256433, -0.3095228 , 0.3627241 ],
[ 0.00684866, 0.35363927, 0.11069642]])
'''
# 确保结果正确,即转换后均值为0
np.allclose(X_new.mean(axis=0), np.zeros(X_new.shape[1]))求X_new的协方差矩阵C
C = np.dot(X_new.T, X_new) / (X_new.shape[0] - 1)
'''
C
array([[ 0.10488363, -0.02467955, -0.10903811],
[-0.02467955, 0.16369454, 0.05611495],
[-0.10903811, 0.05611495, 0.13564834]])
'''求C的特征值和特征向量,这里用的是numpy的特征分解函数
eig_vals, eig_vecs = np.linalg.eig(C)
'''
eig_vals
array([0.26474535, 0.00779743, 0.13168373])
eig_vecs
array([[-0.53801107, 0.72610049, -0.42816139],
[ 0.50584138, -0.12820944, -0.85304562],
[ 0.67429117, 0.67552974, 0.29831358]])
'''求X的PCA结果,就是X右乘k阶特征向量。这里k还是取的3。
X_pca = np.dot(X_new, eig_vecs)
'''
array([[-0.41894072, 0.05880142, -0.38780564],
[ 0.58905292, -0.10265648, -0.07453908],
[-0.64922927, -0.08462316, 0.24926273],
[ 0.22927473, 0.09406657, 0.4846625 ],
[ 0.24984234, 0.03441165, -0.27158052]])
'''numpy的SVD求PCA
首先,直接求X_new的SVD,同样使用numpy的函数
# 注意这里的Vh其实是公式中的VT
U, Sigma, Vh = np.linalg.svd(X_new, full_matrices=False, compute_uv=True)
'''
U
array([[-0.40710685, 0.53434046, 0.33295236, 0.59843699, -0.28241844],
[ 0.57241386, 0.10270414, -0.58127362, 0.5471169 , -0.15677466],
[-0.63089041, -0.34344824, -0.47916326, 0.32579597, 0.38507162],
[ 0.22279838, -0.66779531, 0.53263483, 0.46842625, 0.03587876],
[ 0.24278501, 0.37419895, 0.19484969, 0.13026931, 0.86376738]])
Sigma
array([1.02906823, 0.72576506, 0.17660612])
Vh
array([[-0.53801107, 0.50584138, 0.67429117],
[ 0.42816139, 0.85304562, -0.29831358],
[ 0.72610049, -0.12820944, 0.67552974]])
'''我们来根据上面的公式,确认下eig_vals和S的关系,注意在numpy的实现中,特征值和奇异值的排序是不同的
np.allclose(eig_vals, np.square(S) / (X_new.shape[0] - 1))
'''
eig_vals
array([0.26474535, 0.00779743, 0.13168373])
np.square(S) / (X_new.shape[0] - 1)
array([0.26474535, 0.13168373, 0.00779743])
'''从结果看出,确实跟公式是一致的。 接下来用SVD求PCA就简单了,直接右乘V即可。
# 注意Vh是公式中的VT,因此V=Vh.T
X_pca_svd = np.dot(X_new, Vh.T)
# X_pca_svd = np.dot(U, np.diag(Sigma))
'''
X_pca_svd
array([[-0.41894072, 0.38780564, 0.05880142],
[ 0.58905292, 0.07453908, -0.10265648],
[-0.64922927, -0.24926273, -0.08462316],
[ 0.22927473, -0.4846625 , 0.09406657],
[ 0.24984234, 0.27158052, 0.03441165]])
'''求出结果后,正当我们信心满满的对比一下X_pca和X_pca_svd,以为大功告成打完收工时,却发现二者是不一致的。WTF?
结果分析
仔细研究下X_pca和X_pca_svd的结果,可以看出,排除特征值和奇异值的排序导致的列向量顺序不同外,部分列向量的绝对值相同但正负不同。
问题出在哪里?我们搬出Scikit Learn,再来算一次PCA:
from sklearn.decomposition import PCA
pca = PCA(3)
pca.fit_transform(X) # sklearn自动处理去均值化
'''
array([[ 0.41894072, -0.38780564, -0.05880142],
[-0.58905292, -0.07453908, 0.10265648],
[ 0.64922927, 0.24926273, 0.08462316],
[-0.22927473, 0.4846625 , -0.09406657],
[-0.24984234, -0.27158052, -0.03441165]])
'''嗯,也是绝对值相同但正负不同。都说Scikit Learn的PCA就是SVD做的,难道是骗人的? 好在代码不会骗人,我们直接翻出源码。
通过研究Scikit Learn的源码svd_flip@scikit-learn/extmath.py找到了答案: SVD奇异值分解的结果是唯一的,但是分解出来的U矩阵和V矩阵的正负可以不是唯一,只要保证它们乘起来是一致的就行。因此,sklearn为了保证svd分解结果的一致性,它们的方案是:保证U矩阵的每一行(u_i)中,绝对值最大的元素一定是正数,否则将u_i转成-u_i,并将相应的v_i转成-v_i已保证结果的一致。
这又是数学与工程的问题了。在数学上,几种结果都是正确的。但是在工程上,有个很重要的特性叫幂等性(Idempotence)。
Methods can also have the property of “idempotence” in that (aside from error or expiration issues) the side-effects of N > 0 identical requests is the same as for a single request.
这是源自于HTTP规范中的一个概念,可以引申至各种分布式服务的设计当中,即:高质量的服务,一次请求和多次请求,其副作用(结果)应当是一致的。Scikit Learn正是通过svd_flip这个函数,把一个数学上并不幂等的操作,转化成了幂等的服务,其设计之讲究可见一斑。
总结
本文通过公式推导和numpy代码实战,展示了PCA的正常解法,以及工业界常用的SVD解法,并最后引申至数学和实现的一些探讨。“part-science, part-art”,这就是我最喜爱的机器学习之道

