终身持续学习-可塑权重巩固（Elastic Weight Consolidation）

回过头来梳理了一下EWC方法，在持续终身学习里面很经典的一个方法，Deepmind写的晦涩难懂x，当时折腾了好久才理解。。。。。因为自己有点菜√

条件和目标

论文中，假设存在两个任务A和B (可以推广为旧任务和新任务)，数据集分别为D和D。模型学习完任务A后，继续学习任务B，并且不再使用任务A的数据，只使用任务B的数据。我们想让模型在这种情况下学习完任务B后，能够在任务A和B上都有不错的表现。

问题分析

在实际环境中，未来的任务和数据是无法预测的，在时间轴上，任务的数据是非独立同分布 Non-IID.，本质上，这是一个时域上的 Non-IID. 问题。目前通常训练模型，都是随机打乱数据，使得其近似成 IID.，但在序贯学习(Sequential Learning)里面，没有太多的内存来存旧数据，并且未来的数据是未知的，难以用同样的策略转化为 IID.，如果不用额外内存来存储旧任务的数据并且采用相同策略来训练模型，那么模型将会发生灾难性遗忘(Catastrophic forgetting)，因为新任务的数据会对模型造成干扰(interference)，模型参数不受限地变动使得模型会遗忘旧任务上学习到的知识。核心问题在于，如何用可接受的代价来减缓灾难遗忘？

举个栗子

任务A是猫狗识别二分类，任务B是狮虎识别二分类，训练完猫狗识别后，模型在猫狗识别的任务上有很不错的表现，这个时候，直接用这个模型继续去训练狮虎识别(此处默认只用狮虎数据集)，那么模型在猫狗识别任务上的表现，将会变得很差，这个过程中，模型遗忘了识别猫狗的能力，发生了灾难性遗忘。终身持续学习的目标是想让模型继续训练识别狮虎的时候，还能保留拥有识别猫狗的能力。

EWC的解决方法

下面都是针对神经网络讨论。

简单地说，EWC从新任务数据对模型的interference角度，让模型参数受限地变动，阻碍在旧任务上重要参数的变化。比如，参数矩阵里面，某些参数对猫狗识别非常重要(这些重要参数在确定分类器分类猫狗的超平面过程中起主要作用)，那么在训练狮虎识别时，记下这些参数原本的值，加一个损失函数阻碍它们的变化(参数像橡皮筋有弹性一样，想拉长它，会有弹力阻碍)，模型在样本空间中，猫狗识别的数据样本区域分类器的超平面变化不大。

EWC加了一个正则化损失函数：

\mathcal{L}_{old} = \frac{\lambda}{2} \sum_{i} \Omega_{i} \left(\theta_{i}-\theta_{i}^{*}\right)^{2} \tag{1}

\Omega_{i} 代表了参数 \theta_{i}^{*} 在任务A(旧任务)上的重要性,，就是论文里说的费雪信息矩阵的对角。 \lambda 是权重调节因子。

其中，这里的 \theta 和 \theta^{*} 是长度为 N 的一维向量， N 是模型的参数总数(把所有参数矩阵都拿出来，然后平铺在一起)。

参数重要性的估计

EWC方法里，参数的重要性用二阶导来评估。

\Omega_{i} = \frac{1}{\mid D \mid} \sum_{d \in D} \frac{\partial^2 \mathcal{L}(d,\theta)}{\partial \theta^{2}} \tag{2}

D是数据集。 \mathcal{L} 是任务的损失函数，比如猫狗识别一般就用交叉熵。 \mathcal{L}(d,\theta) 为参数为 \theta 的模型和一个数据样本 d 上的损失。

为了降低计算复杂度，按照Theory of Point Estimation, Second Edition by Lehmann & Casella, Lemma 5.3, p. 116.，做了个近似：

\Omega_{i} = \frac{1}{\mid D \mid} \sum_{d \in D} \frac{\partial \mathcal{L}(d,\theta)^{2}}{\partial \theta^{2}} \tag{3}

这个近似仅限于参数在极值点附近，或者说模型在该数据集上训练好了，到了最优。

看到这很简单，就是用梯度的平方平均值来作为重要性，如果只是要用这个方法的话，这里就够了，下面都是理论推导。

贝叶斯视角下EWC的理论推导

机器学习在贝叶斯的视角下，目的都是为了最大化后验概率 p(\theta | D) ,但是因为后验概率难以估计(不可能尝试所有的 \theta )，因此用贝叶斯公式 p(\theta | D)=\frac{p(D | \theta)P(\theta)}{P(D)} 转化为最大化 p(D | \theta) ，然后取一个 log 转成似然函数用点估计方法做极大似然估计来达成目的。

在这里，我们把 D 分为 D_{A} 和 D_{B} ，因此：

\begin{aligned} \log p(\theta | D) &= \log p\left(D_{A}, D_{B} | \theta\right)+\log p(\theta)-\log p\left(D_{A}, D_{B}\right) \\ &=\log p\left(D_{A} | \theta\right)+\log p\left(D_{B} | \theta\right)+\log p(\theta)-\log p\left(D_{A}\right)-\log p\left(D_{B}\right) \\ &=\log p\left(D_{B} | \theta\right)+\log p\left(\theta | D_{A}\right)-\log p\left(D_{B}\right) \end{aligned} \tag{4}

因此，我们的目标在贝爷看来，只是一边最大化任务B的似然概率 p\left(D_{B} | \theta\right) ，一般保持任务A的后验概率 p\left(\theta | D_{A}\right) 的最大化。最大化任务B的似然概率推导到后面任务的损失函数，这个推导就不展开讲(但是都是类似的)，下面推导保持任务A的后验概率的最大化的损失函数。

先拉普拉斯近似，假设p\left(\theta | D_{A}\right)关于参数服从高斯分布，均值为 \mu ，方差为 \sigma ，都是是长度为 N 的一维向量。

把p\left(\theta | D_{A}\right)写作一个关于 \theta 的函数：

p\left(\theta | D_{A}\right) = \frac{1}{Z}f(\theta) \tag{5}

其中， Z 为归一化系数(概率的积分必须为1)，不用管它。

然后，对它的似然函数进行泰勒展开(log和ln在这里没有本质区别)：

\ln f(\theta)=\ln f\left(\theta^{*}\right)+J_{\ln f}\left(\theta^{*}\right) \cdot\left(\theta-\theta^{*}\right)+\frac{1}{2} \cdot\left(\theta-\theta^{*}\right)^{T} \cdot H_{\ln f}\left(\theta^{*}\right) \cdot\left(\theta-\theta^{*}\right)+R_{n}(\theta) \tag{6}

\theta^{*} 为在任务A上优化好的参数，另外复习一下泰勒展开公式。。。。：

F(x)=\frac{F\left(x_{0}\right)}{0 !}+\frac{F^{\prime}\left(x_{0}\right)}{1 !} \cdot\left(x-x_{0}\right)+\frac{F^{\prime \prime}\left(x_{0}\right)}{2 !} \cdot\left(x-x_{0}\right)^{2}+R_{n}(x)

F(x)=\frac{F\left(x_{0}\right)}{0 !}+\frac{J_{F}\left(x_{0}\right)}{1 !} \cdot\left(x-x_{0}\right)+\left(x-x_{0}\right)^{T} \cdot \frac{H_{F}\left(x_{0}\right)}{2 !} \cdot\left(x-x_{0}\right)+R_{n}(x)

因为在任务A上，模型优化到了最优，损失函数很小，一阶导很小，近似为0，并且三阶及以上的项，在 \theta 变化不大的情况下都可以近似为0，因此只保留二阶项和零阶项。

\ln f(\theta) \approx \ln f\left(\theta^{*}\right)-\frac{1}{2} \cdot\left(\theta-\theta^{*}\right)^{T} \cdot F_{\ln f}\left(\theta^{*}\right) \cdot\left(\theta-\theta^{*}\right) \\ F_{\ln f}=-H_{\mathrm{lnf}}\left(\theta^{*}\right) \tag{7}

这里，把Hessian矩阵取负，就得到了费雪信息矩阵。

对公式(7)取指数，得：

f(\theta) \approx \frac{1}{Z} f\left(\theta^{*}\right) \cdot e^{-\frac{1}{2}\left(\theta-\theta^{*}\right)^{T} \cdot F_{\operatorname{lnf}}\left(\theta^{*}\right) \cdot\left(\theta-\theta^{*}\right)} \tag{8}

看，活脱脱的高斯分布。

因此，回头看我们一开始的假设， p\left(\theta | D_{A}\right) ，它是服从一个 \mu=\theta^{*} ， \frac{1}{\sigma^{2}}=F_{lnf}(\theta^{*}) 的高斯分布，而最大化 p\left(\theta | D_{A}\right) 就等价于最大化 \ln f(\theta) 。

因为 \ln f\left(\theta^{*}\right) 是个常数( \theta^{*} 是给定的)，因此，最大化 p\left(\theta | D_{A}\right) 最终等价于最大化 -\frac{1}{2} \cdot\left(\theta-\theta^{*}\right)^{T} \cdot F_{\ln f}\left(\theta^{*}\right) \cdot\left(\theta-\theta^{*}\right) 。

此外，\theta^{*}都是长度为 N 的一维向量， F_{\ln f}\left(\theta^{*}\right) 为 N\times N 大小，计算的时间和空间复杂度难以接受，于是和优化的领域一样，取了费雪信息矩阵的对角线，这等于假设参数之间相互独立没有影响，最终，导出损失函数：

\mathcal{L}_{old} = \frac{\lambda}{2} \sum_{i} F_{\ln f}\left(\theta^{*}\right)_{i,i} \left(\theta_{i}-\theta_{i}^{*}\right)^{2} \\ F_{\ln f}\left(\theta^{*}\right)_{i,j} =\frac{\partial^{2} \mathcal{L}(d,\theta)}{\partial \theta_{i} \partial \theta_{j}} \tag{9}

看完后应该会有不少人联想到L2正则化，确实，本质上他们都是针对参数先验进行构造，假设和推导也很类似，这也是目前ML领域水论文的方向之一。

实验

这个领域目前的Benchmark并不多，普遍是基于原有的Benchmark进行构造，经典的构造方法有重排列(Permute)数据集、分割(Split)数据集。

Permuted MNIST 是一个基础的Benchmark，它将MNIST里面每张图片向量化后进行重排列，其实就是用一组随机索引来打乱向量里面每个元素的位置，不同的随机索引打乱后产生不同的任务。

论文里的实验结果我就不贴了，贴一下我自己跑的，截自自个的论文。。。SI、MAS都是类似的方法，PI+ALE是自个之前水的一个方法。

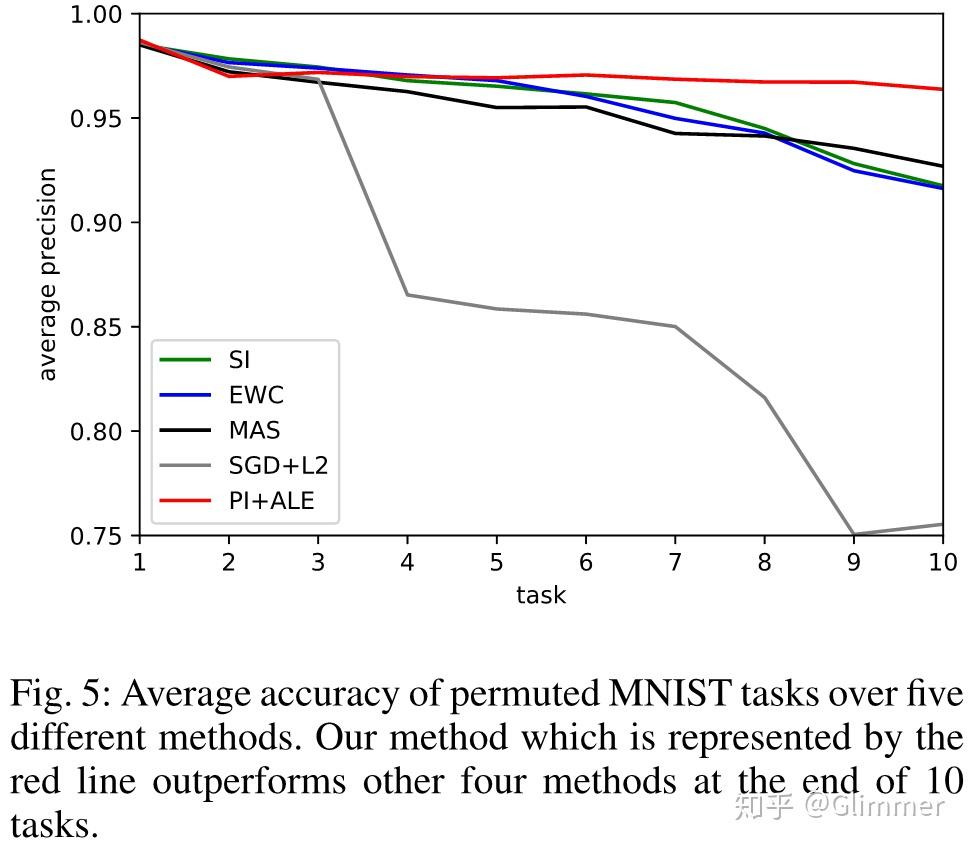
效果比SGD好很多，还是很有效的。

Split MNIST 和 Disjoint MNIST 类似，前者把MNIST分割为标签为(0,1)、(2,3)、(4,5)、(6,7)、(8,9)的5组任务，后者则分为标签(0,1,2,3,4)、(5,6,7,8,9)两组任务。在这类数据集上要注意模型是单输出层(Single head)还是一个任务一个输出层(Multi-head)。EWC方法上Multi-head的结果平均精度接近99%(除了SGD其他方法都接近99%)，而Single head的实验现象很奇怪，一开始测的很高(有88%的)，然而后面再怎么跑，EWC都和SGD差不多，把旧任务遗忘了。

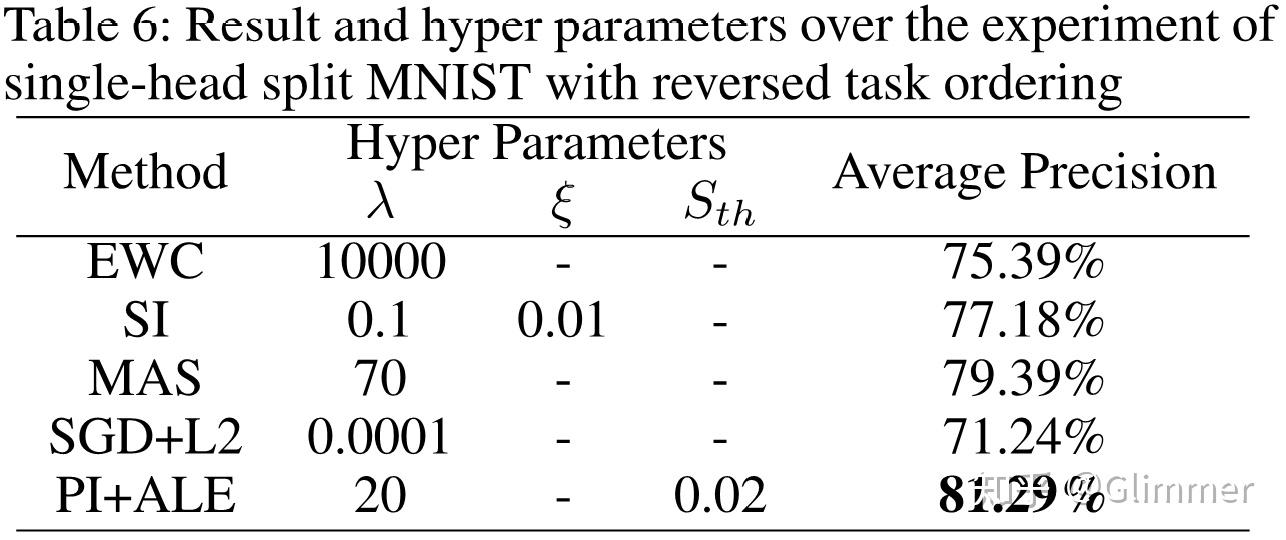
结论

在任务差异不大情况下，EWC确实是一个有效的方法，理论也很优雅，但任务差异较大时，泰勒展开的高阶项就不能近似为0，导致了EWC方法不好的表现，此外，参数之间是有关联分布的(假设应该他们是混合高斯)，EWC取费雪信息矩阵的对掉线忽略了参数相关性，这些都是EWC的不足，后续有一些论文多多少少改进了一些，但任重道远~

引用什么的其他的以后再补充8 √