并行算法科普向 系列之三：归并与归并排序，过滤与快速排序

（本文作者为 Yihan Sun，转载请注明出处）

前面两讲里面我们讲了一些基础的并行算法和套路，随着我们学了的东西越来越多，我们马上也就能解决越来越复杂的问题啦。所以下面的两讲，我们来看一看排序算法。

0 串行排序算法

这一段我们只是来复习一下串行算法，基础比较好的同学们可以直接跳到下一段。

我们这一讲主要是说基于选择的排序。也就是说我们通过比较的方式确定两个数的大小关系，然后通过移动或者交换的操作把每个数摆到该放的地方去。对于一个长度为 n 的任意排列，基于比较的排序算法至少要比较 O(n log n) 次。这个事情你大致上可以简单地这样理解。每对两个元素 x 和 y 做一次比较有两种情况，一种是 x 大，一种是 y 大，那么这个世界上有 n! 种不同的排列，通过确定 x 和 y 的大小关系，可以排除其中的一半。就算你每一次比较都精心挑选两个元素，一次比较也只能排除所有情况中的一半。所以一共就要 log_2(n!) 这么多次比较。这个数差不多就是 O(n log n)。

串行来说，想通过 O(n^2) 的复杂度做到一个排序算法是非常容易的。比如选择排序，它就把所有元素全扫一遍，发现最小的，摆第一个，然后剩下元素扫一遍，发现它们中最小的，摆下一个，一直这样 O(n^2) 次就能把整个数组都安排得明明白白。

那想做到 O(n log n) 也不难，我们这里重点讲两种算法，一种叫归并排序，一种叫快速排序。

0.1 归并排序

归并排序的思路是这样的：它把数组平分成左右两部分，分别排个序，然后就得到了两个长度为 n/2 的已经排好序的数组。最后把它们合起来。所以这个算法要解决的最重要的问题就是，怎么把两个已经有序的数组合并呢？串行的合并 (merge) 算法是这样的：

对两个数组 A 和 B 各维护一个指针 pa 和 pb，一开始都在数组头。每一次我们比较一下这两个指针指的元素，比方说 A[pa]<B[pb] 吧，那就把 A[pa] 写到输出数组里，然后 pa 移到下一位。反之也是一样的。总之每一次，把比较小的那个写到输出数组的下一位，直到全部写完。

Merge(A, B, n) {
  p1 = 0; p2 = 0; p3 = 0;
  while ((p1 < n) && (p2< n)) {
    if (A[p1] < B[p2]) {
      C[p3] = A[p1]; p1++
    } else {
      C[p3] = B[p2]; p2++;
    } }
  //copy the rest of the unfinished array
  return C;
}

举个例子来讲底下这个图就是在这两个指针变化的过程中，逐渐把数写到输出数组里的一个示意图。

那这个算法如果合并两个长度为 m 和 n 的数组，就是 O(m+n) 的时间，因为它会（也仅会）把每个元素扫一遍。那么回到归并排序的问题上来，它一共会花 O(log n) 轮，每一轮 merge 的总花费啊，就是 O(n)。所以加起来是 O(n log n)。

但是这个算法呢它有个小问题，就是上面这个归并的过程啊，它要新开一个数组，把所有元素都拷贝一遍。而且我们有三个指针把三个数组都捋了一遍。所以呢，也是因为 I/O efficiency 的问题，实际中呢，它没有快速排序快。所以我们下面看看快排是什么。

0.2 快速排序

快速排序顾名思义，就是它特别快。它的思路是这样的，从所有的数中先随便取一个，我们管它叫 pivot，就叫它 x 吧。然后这个算法对着这个数组一通操作猛如虎：把所有比 x 小的数放到左边，剩下的（大于等于 x 的）放右边，完后把左边排好序，右边排好序，诶这不巧了吗不是，它不就全排好序了吗。所以这个过程它差不多是这样的：

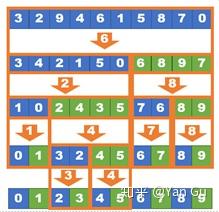
这里橙色箭头里的数就是我们选择的 pivot。这个 pivot 是什么并不太重要，随机选就可以。你看每次一个步骤结束，它这个数组都会很粗放地被 sort 一下：数组会被分成几块，每一块都是乱的，但是块和块之间的顺序已经确定了。当这个“块”分得越来越细，整个数组就全排序好了。所以这个算法要解决的最重要的问题就是，怎么把数组里的数按照 x 分界，把比 x 小的移到一边，剩下的移到另一边。这件事呢，它是这么解决的：

首先，我们还是维护两个指针 p1 和 p2，一个在数组第一个元素，一个在最后一个元素。

然后，我们看 p1 指的元素，如果它比 x 小，我们就把它放那儿，因为它本来就应该在左边，然后 p1 往前移一个接着看，直到发现了一个元素它比 x 大。这说明这个数的位置不对，它应该在右半边啊。

然后，对 p2，同理，我们看它如果比 p 大，就放那儿，把 p2 往回走一个，直到 p2 指的数比 x 小为止。这说明这个数应该在左半边的，结果它现在在右边。

然后我们一看，p1 指的数应该在右边结果在左边，p2 指的数应该在左边结果在右边。诶这不巧了吗不是，那把他俩换一下不就都解决了吗。

于是我们把他俩换过来。然后接着找下面两个放错位置的元素，交换。这个过程什么时候中止呢，就是这两个指针碰上的时候，于是每个数都在自己该在的位置啦。那这里就是一个示例图：

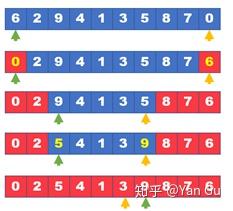
蓝色是原始数组，红色就是说我们扫过了这个点发现它没问题可以放那儿，黄色的数字是说现在我们发现了一个放错位置的数，准备交换。当橙色和绿色的箭头位置颠倒的那一天，就是算法完成的时候。

所以这个过程需要多久呢，这两个箭头加起来也是把每个元素扫了一遍，所以是 O(n) 的。那快速排序需要多少轮呢？虽然这个 pivot 它可以是任何数，不一定把数组分得很均衡，但是还是可以证明，只要这个 pivot 是纯随机地从这些元素里取的，那么 with high probability (whp) 花 O(log n) 轮就能到达 base case。你可能一次运气很差选到了最小的元素当 pivot，但你很难运气一直很差。这个 whp 是什么意思呢，你可以理解为这个算法 c log n 轮还没结束的概率是 O(1/n^c)，也就是说，它 5log n 轮还不结束的概率不到 O(1/n^5)，10log n 轮还不结束的概率不到 O(1/n^10)，花得轮数越多越不可能。虽然在你非常倒霉的情况下整个算法还是有可能是 O(n^2) 的，但是你想这你得多倒霉啊。

这个算法和归并排序比，主要的优势有两条，一个是它是 in-place 的，它这些元素挪来挪去，但是并没用到额外空间。二是它每一个 recursive call 都在一个连续的区块内操作，这些被操作的元素彼此离得很近。这两者总体都是讲它的 locality 比较好。所以跑起来会快很多。

好啦这就是我们对串行算法的回顾。那这两个算法怎么并行一下呢？首先，我们发现两个算法都用了分治，都分成了两个（互不影响的）子问题递归。那就把这两个子问题并行一下好了！应该很好并行才对啊！那我们就来一个一个看一下吧！

1 归并排序与归并

让我们先看看直接把归并排序的两个子问题并行一下，会得到什么。这不会对算法的 work 造成影响。那 depth 呢？首先，第一步合并它们要花 O(n) 的时间，第二步两边分别是需要 O(n/2) 的时间，第三部是 O(n/4)，以此类推，加起来是 n+n/2+n/4…=O(n)。

Hmmm...O(n) 这恐怕不是很行吧。所以要做好归并排序，我们同样要解决的问题是，怎么归并 (merge)？

1.1 归并算法

现在我们有了两个有序的数组，怎么把它并行地合并成一个数组呢？让我们还是从我们最熟悉的分治方法入手。首先，我们能不能把问题分成一样大的两个子问题呢？

既然我们的输入是两个数组，我们要先定义好这个“一样大”。如果只是简单的把其中一个数组均分，那另一个数组对应的规模可能并不是一半一半（插一句，其实这样做也可以得到一个类似的算法，bound 也是相同的，但是分析起来有点麻烦，所以我们这里介绍下面的这个版本）。那不如按照输出数组看吧！我们先把输出数组均分两半，反过来看，它的左边对应 A 里的开头到中间某个位置 m1，与 B 里的开头到中间某个位置 m2，的所有元素的合并。它的右边同理，是 A 里从m1+1 到结尾与 B 里 m2+1 到结尾的合并。如下图所示，我们要在 A 里和 B 里分别找到一个分割点，在此之前的点都在输出的前半截，在此之后的点都在输出的后半截。

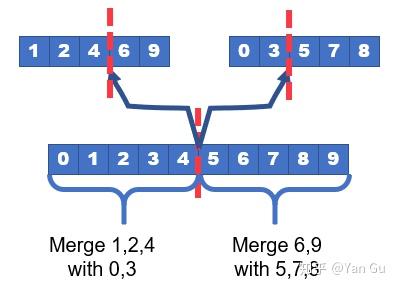
下面的问题就是：给定两个有序数组，怎么找到整体的中位数，以及这个中位数在两个数组里对应的下标（分割点）呢？

这个世界上是有算法可以做这件事的，这个算法只要花 O(log (n+m)) 的时间就能在两个长度为 n 和 m 的数组上做到这件事了（事实上，我们可以用 O(log (n+m)) 的时间在两个大小分别为 n 和 m 的数组上，对任意 k，找到整体的第 k 个数）。这个算法本身不是并行的，因为它复杂度已经是 log 级别了没什么必要并行，但是这个算法在并行算法里很！有！用！如果你不熟悉这个算法，我们在 1.2 这一章会给大家介绍一下。

所以当我们可以花 log(n+m) 的时间做到找中位数，我们自然也可以把这个数分别定位到两个数组，也就是对两个数组都找到这个所谓的分界点。那现在我们的算法和复杂度是什么样呢？

//A and B are input arrays, C is the output, na and nb are sizes of A and B
merge(A, B, na, nb, C) {
  if na+nb=0, copy the only element to C
  //sa and sb are the splitters of the global median in A and B, respectively
  (sa,sb) = mid_splitter(A, B, na, nb);
  in parallel:
    merge(A, B, sa, sb, C);
    merge(A+sa, B+sb, na-sa, nb-sb, C+sa+sb);
}

这里这个 mid_splitter 就是说，对两个数组，找到它的中位数，并返回这个中位数分别在这两个数组的什么位置。注意上面的 base case，我们说当俩数组加起来只有一个数的时候我们才停，其实当然当其中一个数组是空的时候我们就可以停下来了，然后并行地把另一个数组的所有数 copy 到 C 里。这里为了分析和叙述方便我们用上面那个简单粗暴的版本。

那这个算法的复杂度怎么分析呢？首先，我们要分析这个问题，写递推式，我们要确定问题规模是什么。我们这里把问题规模 N 当做 A 和 B 规模的总和，也就是输出 C 的规模。那么经过一次递归，问题分成了两个（基本上）完全一样大的子问题（因为我们找了全局中位数啊）。在递归之外我们做的唯一一件事，就是，我们找了这个中位数，花了 O(log(n+m)) 也就是 O(log N) 的时间。那这个问题的 work 和 depth 就是这样的：

W(N)=2W(N/2)+O(log N)

D(N)=D(N/2)+O(log N)

这个嘛解出来就是 W(N)=O(N), D(N)=O(log^2 N)。

事实上，我们用类似的方法，可以把这个归并算法的复杂度降低到 O(log N) 的 depth。其中的关键也是利用这个寻找第 k 大的数作为 subroutine。这里呢，我们不讲这个 O(log N) depth 的算法了，为什么呢因为这是一道思考题！哈哈哈哈哈哈哈~

（这真的是一些已有课程的作业题，所以我就不细讲了。事实上有多种办法可以把 merge 这个算法的 depth 变成 O(log n)。大家可以自己动动脑筋哦）

1.2 寻找全局第 k 个元素

好了那上面合并算法的关键就是说我们得有一个算法，给定两个有序数组大小为 n 和 m，找出其中整体排位是 k 的数 x，并且返回这个 x 在两个数组中的位置分别是哪儿。这个算法花时要是 O(log (n+m))。当然，从渐进的角度来讲，我们只要把这个 x 找出来，再在那两个数组里 binary search 一下就行了，不会影响渐进复杂度。

这个算法本身也是基于二分查找的。我们可以管它叫 dual binary search，因为它在两个数组上同时 binary search。它是这样做的：

首先，我们找出 A 数组和 B 数组的中位数，也就是 A[n/2] 和 B[m/2]，分别设为 x’和 y’ 吧。不失一般性我们假设 x' < y'。那么由于 x' 比较小，我们可以得到什么呢？我们可以知道在两个数组里比 x' 小的数最多有 (n+m)/2 个，也就是 A 里 x' 之前的所有数，和 B 里 y' 之前的最多 m/2 个数，因为 y' 已经比 x' 大了，所以 B 的后半段不会比 x' 小了。同理我们知道最多有 (n+m)/2 个数能比 y' 大。

然后我们比较 k 和 (n+m)/2 的大小。如果 k<(n+m)/2，考虑到比 y' 大的数最多只有 (n+m)/2 个，它们肯定不会是前 k 个数。那所有比 y' 大的数我们就不用考虑了。那哪些数坐实了比 y' 大呢，就是 B 的后半截 B[m/2+1, …, m] 啊！因此我们可以排除 B 数组的一半，然后递归。同理我们可得 k>=(n+m)/2 的情况，这时所有比 x' 小的数都可以排除，也就是 A[1, … , n/2]，然后在递归中我们要找的数变为 k-n/2 大的。

（以上所有 m/2 之类的数都是伪代码式的大概，具体还有加一减一之类的细节大家自己体会一下哦）

如果 x' >= y' 我们也可以类似地去做，最终排除掉 A 和 B 其中一个数组的一半。

这几种情况下，我们总可以把某一个数组的规模缩减到原先的一半。到什么时候停呢？A数组的规模最多减小 log n 轮就只剩一个数了，此时我们可以进行常规的二分查找找到这个元素在 B 中的位置然后直接找到第 k 大的数。同理 B 数组的规模最多只能减小 log m 轮。总的时间复杂度于是就是 O(log m + log n)=O(log (m+n)) 了。所以在 O(log (n+m)) 的时间内，我们就会找到这个 x 啦。

1.3 并行归并排序

那么把上面的算法用在归并排序里，我们就会得到一个 O(n log n) work 和 O(log^3 n) depth 的排序算法了！不错不错！我们终于有一个 work-efficient 并且 polylog depth 的排序算法了！

事实上，正像上面说的，我们也可以把归并排序的归并算法做到 O(log n) depth，这会给出一个 O(log^2 n) depth 的排序算法。

值得一提的是，这个归并算法本身，包括那个寻找第 k 个元素的算法，即便脱离了归并排序，也是非常有用的。在今后的别的算法里，我们也会用到它们。

2 快速排序

那我们下面来看看快排吧！作为串行排序中大家最喜欢的算法（之一？），快排要怎么并行呢？同样地，如果我们直接把两个分治递归并行地跑，是不能得到很好的 depth 的——考虑那个一头一尾两个指针不停交换元素的移动算法，它本身就要 O(n) 的时间，还很不好并行。所以我们要把快排并行，就是要设计一个并行算法，它把一个数组按照 x 分成两部分，小的放左边大的放右边。

串行的时候，我们用了个很巧妙的方式，把这两件事一起做成了。那如果我们现在就一件一件地做呢？先把比 x 小的数挪好，看看怎么做。

首先，我们得找出这些数，它们散落在数组的各个角落，不过这很容易，一个 parallel_for 就搞定了。我们可以用一个和原数组一样长的 flag 数组标记这个数我们要不要留它，如果它比 x 小，我们给 flag 数组对应位置设成 1，否则设成 0。所以我们现在就是要做个过滤 (filter) 操作！把所有 flag 是 1 的对应位置的数找出来！

那把别的元素都去掉好说，我们把剩下的数都标成什么空元素就好了。

但是它们还是在原来的位置啊。我们想让他们都在数组最左边，得连着。这个过程呢，我们称为 pack 操作。就是把中间隔着无意义元素的一个松散的数组啊，它 pack 起来。

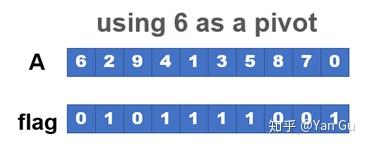
只要我们知道每个数都在哪儿，写过去是很容易的，那么 2 这个数它应该在哪儿呢？他应该在输出数组的第一个，那 4 应该在哪儿呢？它应该在第二个。1 应该是第三个，3 应该是第四个，以此类推。要是我们知道这件事，我们就再 parallel_for 一下，各自写去目标位置就行了。那怎么知道这件事呢？为什么 3 这个数应该放第四个呢？因为它前面有三个有意义的数，flag 数组在它之前，有三个 1 了。这事听着是不是很熟悉，这不就是前缀和嘛！！

所以我们对 flag 这个数组调用一个前缀和，就得到：

那些 X 位置对应的前缀和是没有意义的，因为它们的 flag 是 0，反正我们也不管它们。剩下的位置上，前缀和代表了要写去的输出数组的下标。也就是说，伪代码是这样写的：

filter(A, flag, n) {
  ps = scan(flag);
  parallel_for(i=1 to n) {
    if (ps[i]!=ps[i-1])
      B[ps[i]-1] = A[i]; //这里 -1 是因为下标从 0 开始
  }
}

呐，它这个 scan 花了 O(n) 的 work 和 O(log n) 的 depth。它然后直接一个 parallel_for 也是 O(n) 的 work 和 O(log n) 的 depth。所以这个 filter 也是 O(n) 的 work 和 O(log n) 的 depth。

呐，所以最后我们就可以得到一个 quicksort，它依然是 whp 需要 O(log n) 轮结束。每一轮啊，我们对每个子问题都做一个这样的 filter，对吧。考虑到这个 filter 是 O(n) 的 work 和 O(log n) 的 depth，整个quicksort 就是 O(n log n) 的 work 和 O(log^2 n) 的 depth 啦。

值得一提的是，这个并行的快排，和上面的归并排序比，它就“快”得不那么明显了。其中一个原因就是，因为需要 filter，快排也需要开额外空间了，所以之前 locality 上的优势便不复存在。因此在实际中我们经常使用的并行排序算法叫 sample sort，这个会在下节再讲。

3 能把 depth 降到 O(log n) 吗？

能！但是，again，这要看你的计算模型。在PRAM上，著名的 Cole's merge sort 就是 O(n log n) 的 work 和 O(log n) 的detph，这个算法可以说是当年研究过并行算法的人心中的白月光。它特别复杂精巧，基本上是那时候已知的唯一的能做到 work-efficient + O(log n) depth 的排序算法。但是！很可惜，当你把它放在 binary-forking 的模型下的时候，它竟然就变成 O(log^2 n) 的depth了。在我们自己最近的一篇 paper 里我们提出了一种 binary forking 下的 work-efficient + O(log n) depth 排序算法，但是它需要 test-and-set 和随机数。

不管怎么说，上面这些 O(log n) depth 的算法可以说，都是非常复杂的，复杂到我们基本上不会在一门 graduate-level 的课程里给你们细讲。但是！但是！如果你只是想要把 depth 做到 O(log n)，这事是一点不难的啊。你看啊，我们可以这么做：

现在我们有 n 个数，所以呢，两两组合有 n^2 组大小关系对不，好我们把他们全比了，记下来。这个一共要比 O(n^2) 组数，也就是说呢，花一个 parallel_for，即便在 binary_forking 下也只要 O(log n) depth 就搞定了。

然后啊，知道了这 n^2 组所有的大小关系，从排序的角度来讲，我们相当于就知道了一切。那怎么把每个数写到他们该在的位置呢？对于每个数来讲，与其相关的 n-1 对大小关系告诉了我们有多少个数比它大，多少个数比它小（显然这件事可以用一个并行的 reduce 算法解决）。这就告诉了我们它在所有数里排第几呀！所以我们再花 O(log n) 的时间，对每个数找一下它的排位，这个排序就做完了。

虽然它的 depth 只需要 O(log n)，但是它比较出所有 O(n^2) 个大小关系花了 O(n^2) 的 work ——嗯所以它不 work-efficient。这个事情告诉我们，对于一个问题，我们经常可以通过 work-depth 的 tradeoff 设计出特殊需求的算法。比如这个排序问题我们就可以通过牺牲 work 得到一个 O(log n) depth 的简单算法。

另外值得一提的是，这个算法它牛逼在什么地方呢，还记得我们以前讲计算模型的时候说过，当你说你的算法，bound 等这些东西的时候，要指明你的 model 和你的 model 支持的原子计算，对吧。那时候我们提过说，有一个模型它说我们的并行计算机（而且还真的有过这样的计算机），可以支持 O(1) 的并行 reduce。在这样的计算机下，加上 n-ary forking，这个排序算法的 depth，是 O(1) 的哦！！！

你可能觉得比较出所有 O(n^2) 组大小关系有点耍流氓，并且，在 n-ary forking 下，比较出所有的这 O(n^2) 个大小关系还只要搞个 parallel_for 就行了，常数的 depth，牛逼不，但是更像耍流氓了。但是你仔细地回味一下这个算法，你会发现，它其实就是并行了选择排序。这么一想是不是感到它平凡多了哈哈。

好啦，这就是今天的内容了，在这一讲里我们主要讲了几个经典的排序算法，更重要的是看到了一些在并行算法设计中有用的subroutine，总结一下，我们知道了：

1，并行的归并排序。由此我们学会了怎么并行地合并两个有序数组。

2，并行的快速排序。由此我们学会了怎么并行地 filter 或者说 packing 一个数组。也就是说，给定一个数组，和另外一些信息指明了这个数组里某一个子集的元素，如何并行地将它们“提取”出来，连续地放在另一个数组里输出。

3，我们还知道了怎么并行选择排序——这是一个很具体的事例告诉我们如何在 work 和 depth 之间实现 tradeoff。

好啦，我们这一讲先说到这里。下一讲我们来看看另外两种排序算法：取样排序（sample sort）和基数排序（radix sort）。

最后，冬天就要来了，大家注意保暖哦！如果觉得太冷，有兴趣的同学不妨考虑一下，来 Riverside？嗯？ 在温暖的加州和我们一起研究一下并行算法？

本系列其它文章：