极大似然估计、最大后验估计
好文共享。
1、贝叶斯公式
这三种方法都和贝叶斯公式有关,所以我们先来了解下贝叶斯公式:
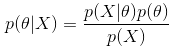
每一项的表示如下:
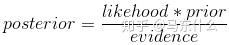
posterior:通过样本X得到参数 \theta 的概率,也就是后验概率。
likehood:通过参数 \theta 到样本X的概率,似然函数,通常就是我们的数据集的表现。
prior:参数 \theta 的先验概率,一般是根据人的先验知识来得出的。比如人们倾向于认为抛硬币实验会符合先验分布:beta分布。当我们选择beta分布的参数
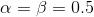
时,代表人们认为抛硬币得到正反面的概率都是0.5。
evidence:
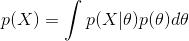
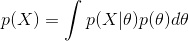
,样本X发生的概率,是各种 \theta 条件下发生的概率的积分(如果离散则就是求和)。
2、极大似然估计(MLE)
极大似然估计的核心思想是:认为当前发生的事件是概率最大的事件。因此就可以给定的数据集,使得该数据集发生的概率最大来求得模型中的参数。似然函数如下:
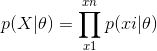
为了便于计算,我们对似然函数两边取对数,生成新的对数似然函数(因为对数函数是单调增函数,因此求似然函数最大化就可以转换成对数似然函数最大化):
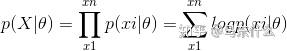
求对数似然函数最大化,可以通过一阶优化算法如sgd或者二阶优化算法如Newton求解。
极大似然估计只关注当前的样本,也就是只关注当前发生的事情,不考虑事情的先验情况。由于计算简单,而且不需要关注先验知识,因此在机器学习中的应用非常广。
mle和loss function的关系
损失函数是作为模型的优化目标的度量。损失函数比单纯的 MLE 更通用。
MLE 是一种特定类型的概率模型估计,其中损失函数是(对数)似然。MLE 是推导概率模型损失函数的一种方法(例如二元交叉熵可由伯努利分布的最大似然公式求解推导而来,mse可以由高斯分布的最大似然公式求解推导而来)。
但是后深度时代,loss function的概念已经非常复杂了,例如多任务学习下就很难使用MLE来进行推导,因此loss function的定义要比单纯的MLE推导出来的部分loss function的定义要更加通用。
3、最大后验估计(MAP)
和最大似然估计不同的是,最大后验估计中引入了先验概率(先验分布属于贝叶斯学派引入的,像L1,L2正则化就是对参数引入了拉普拉斯先验分布和高斯先验分布),最大后验估计可以写成下面的形式:


在求最大后验概率时,可以忽略分母p(X),因为该值不影响对θ的估计。
同样为了便于计算,对两边取对数,后验概率最大化就变成了:
(在极大似然法估计的过程中,因为极大似然假设\theta是一个定值而不是一个随机变量,并不假设它的分布情况而当作一个常量处理所以p(\theta)=1带入map的式子消去就得到了mle的极大似然函数式了)
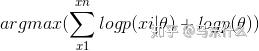
我们和极大似然估计比较一下:
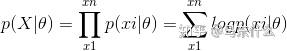
最大后验估计不只是关注当前的样本的情况,还可以灵活加入先验知识(在上式中即为对于模型的参数的分布进行了约束)。
最大后验估计和最大似然估计的区别:
最大后验估计允许我们把先验知识加入到估计模型中,对于逻辑回归,在公式上的表达就是多了一个log P(theta)的项,这在样本很少的时候是很有用的(因此朴素贝叶斯在较少的样本下就能有很好的表现),因为样本很少的时候我们的观测结果很可能出现偏差,此时先验知识会把估计的结果“拉”向先验,实际的预估结果将会在先验结果的两侧形成一个顶峰。通过调节先验分布的参数,比如beta分布的α,β,我们还可以调节把估计的结果“拉”向先验的幅度,α,β越大,这个顶峰越尖锐。这样的参数,我们叫做预估模型的“超参数”。(但是这也和我们选取的先验有关,如果先验的概率选取不当反而会适得其反)
实际上我们平常加入了l1和l2正则化的逻辑回归的损失函数也可以通过最大后验估计的方式推导出来的,具体可见:

其中l2正则化对应的是 \theta 服从高斯分布的先验概率分布,然后把对应的 P(\theta) 代入求解即可,而l1正则化对应的是 \theta 服从拉普拉斯分布。
所以可以看到:
最大似然估计、最大后验概率估计中都是假设 \theta 未知,但却都是确定的值,都将使函数取得最大值的\theta作为估计值,区别在于最大化的函数不同,最大后验概率估计的式子中额外引入了\theta的先验概率,简单来说就是似然函数中多了先验项的乘项,求解的方法上和MLE一样,sgb、newton之类的都可以直接使用。

无论是mle还是map都属于点估计,即我们最终得到的估计参数都是一个固定的值,比如w1x1+w2x2=0.15x1+0.25*x2这种形式。
而在贝叶斯估计中,假设参数\theta是未知的随机变量,不是确定值,以逻辑回归为例,我们不会像使用极大似然估计或者最大后验估计直接得到w1,w2。。。。wn的权重的具体的值而是得到一个关于w(n维)的后验分布——P(w|X),然后用这个分布的期望来作为最终的参数值,因此是分布估计而不是点估计了。举个例子,假设w1服从高斯分布,即

(这里x是w),那么在贝叶斯线性回归中,我们需要估计出这里的u和 \sigma ,得到了w的高斯分布之后怎么预测呢?答案就是我们使用w的高斯分布的期望作为最终的w的估计结果,
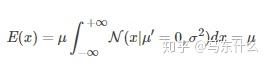
实际上就是原式中的u了。如果w有多个即w1,w2,w3.。。。则问题就转换为多元高斯分布的u(向量)和协方差矩阵 \sum_{}^{}{} 的估计了。
4 贝叶斯估计
简单描述一下贝叶斯估计
那么贝叶斯线性回归具体的计算过程是咋样的呢?这里终于找到一篇写的比较明白的文章了:
感觉这一篇行文脉络比我写的好多了,符号什么的也都统一的比较易懂,直接看一篇就好了。
首先是mle:
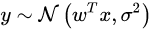
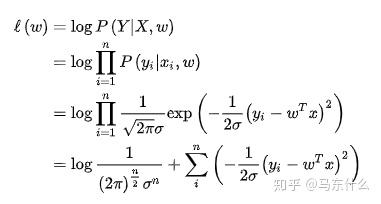
假设y是服从高斯分布的(具体原因可百度)

得到了mse的损失函数的形式。
然后是map:
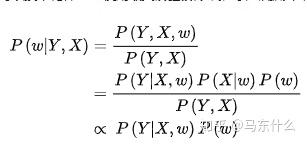
第一步用到了条件概率公式:
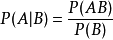
第二步的分子部分用到了全概率公式:(用了两次,自行体会,求和转化为向量形式了所以求和符号没了)
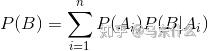
第三步的正比,分子用到了边缘概率密度,具体上文写了,所以忽略不计了。P(X|w)中,X是已知的,所以这一项是一个常数,因为无论w如何变化X都是固定的。
然后:

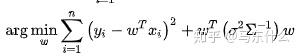
这里就得到了熟悉的l2正则化损失函数的形式了。可以看到似然函数和先验分布都是服从高斯分布的。

