OpenCV图像处理专栏九 | 基于直方图的快速中值滤波算法

BBuf

前言
这是OpenCV图像处理专栏的第9篇文章,主要介绍一个基于直方图的快速中值滤波算法,希望对大家有帮助。
算法原理
传统的中值滤波是通过滑动窗口不断在图像上移动,求出窗口内的中值作为中心像素点的像素。在这个过程中显然存在大量的重复计算,所以效率很低。因此有人提出了一个利用直方图来做中值滤波的算法,如下图所示:
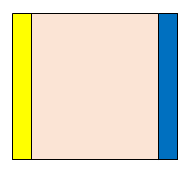
可以把整个图片看成滑动窗口,当我们从左边移动到右边时,中间的粉色部分是共享的,只有黄色部分变为了蓝色部分,所以就想了利用直方图来更新的方法。
算法步骤
- 读取图像I,并且设定滤波窗口大小(winX,winY),一般winX=winY,奇数。
- 设定中值滤波直方图中的阈值,Thresh=(winX*winY)/2 +1;
- 如果要考虑边界情况,可以先对原图像进行扩展,左、右边界分别扩展winX/2个像素,上下边界分别扩展winY/2个像素。
- 逐行遍历图像像素,以第一行为例:先取第一行第一个要处理的像素(窗口中心像素),建立滤波窗口,提取窗口内所有像素值(N=winX*winY个),获取N个像素的直方图Hist。从左到右累加直方图中每个灰度层级下像素点个数,记为sumCnt,直到sumCnt>=Thresh,这时的灰度值就是当前窗口内所有像素值的中值MediaValue。将MediaValue值赋值给窗口中心像素,表明第一个像素中值滤波完成。
- 此时窗口需要向右移动一个像素,开始滤波第二个像素,并且更新直方图。以第二个像素为窗口中心建立滤波窗口,从前一个窗口的灰度直方图Hist中减去窗口中最左侧的一列像素值的灰度个数,然后加上窗口最右侧一列像素值的灰度个数。完成直方图的更新。
- 直方图更新后,sumCnt值有三种变化可能:(1)减小(2)维持不变(3)增大。这三种情况与减去与加入的像素值灰度有关。此时为了求得新的中值,需要不断调整sumCnt与Thresh之间的关系。 (1)如果sumCnt值小于Thresh:说明中值在直方图当前灰度层级的右边,sumCnt就依次向右加上一个灰度层级中灰度值个数,直到满足sumCnt>=Thresh为止。记录此时的灰度层级代表的灰度值,更新MediaValue,作为第二个像素的滤波后的值。 (2)维持不变:说明MediaValue值不变,直接作为第二个像素滤波后的值。 (3)如果sumCnt值大于Thresh:说明中值在直方图当前灰度层级的左边,sumCnt就依次向左减去一个灰度层级中灰度值个数,直到满足sumCnt<=Thresh为止。记录此时的灰度层级代表的灰度值,更新MediaValue值,作为第二个像素的滤波后的值。
- 窗口逐行依次滑动,求得整幅图像的中值滤波结果。
代码实现
#include "stdafx.h"
#include <stdio.h>
#include <iostream>
#include <immintrin.h>
#include <opencv2/opencv.hpp>
using namespace cv;
using namespace std;
//计算中值
int getMediaValue(const int hist[], int thresh) {
int sum = 0;
for (int i = 0; i < 256; i++) {
sum += hist[i];
if (sum >= thresh) {
return i;
}
}
return 255;
}
//快速中值滤波,灰度图
Mat fastMedianBlur(Mat src, int diameter) {
int row = src.rows;
int col = src.cols;
Mat dst(row, col, CV_8UC1);
int Hist[256] = { 0 };
int radius = (diameter - 1) / 2;
int windowSize = diameter * diameter;
int threshold = windowSize / 2 + 1;
uchar *srcData = src.data;
uchar *dstData = dst.data;
int right = col - radius;
int bot = row - radius;
for (int j = radius; j < bot; j++) {
for (int i = radius; i < right; i++) {
//每一行第一个待滤波元素建立直方图
if (i == radius) {
memset(Hist, 0, sizeof(Hist));
for (int y = j - radius; y <= min(j + radius, row); y++) {
for (int x = i - radius; x <= min(i + radius, col); x++) {
uchar val = srcData[y * col + x];
Hist[val]++;
}
}
}
else {
int L = i - radius - 1;
int R = i + radius;
for (int y = j - radius; y <= min(j + radius, row); y++) {
//更新左边一列
Hist[srcData[y * col + L]]--;
//更新右边一列
Hist[srcData[y * col + R]]++;
}
}
uchar medianVal = getMediaValue(Hist, threshold);
dstData[j * col + i] = medianVal;
}
}
//边界直接赋值
for (int i = 0; i < row; i++) {
for (int j = 0; j < radius; j++) {
int id1 = i * col + j;
int id2 = i * col + col - j - 1;
dstData[id1] = srcData[id1];
dstData[id2] = srcData[id2];
}
}
for (int i = 0; i < col; i++) {
for (int j = 0; j < radius; j++) {
int id1 = j * col + i;
int id2 = (row - j - 1) * col + i;
dstData[id1] = srcData[id1];
dstData[id2] = srcData[id2];
}
}
return dst;
}
void MedianFilter(int height, int width, unsigned char * __restrict src, unsigned char * __restrict dst) {
for (int i = 1; i < height - 1; i++) {
for (int j = 1; j < width - 1; j++) {
unsigned char a[9];
a[0] = src[i * width + j];
a[1] = src[i * width + j + 1];
a[2] = src[i * width + j - 1];
a[3] = src[(i + 1) * width + j];
a[4] = src[(i + 1) * width + j + 1];
a[5] = src[(i + 1) * width + j - 1];
a[6] = src[(i - 1) * width + j];
a[7] = src[(i - 1) * width + j + 1];
a[8] = src[(i - 1) * width + j - 1];
for (int ii = 0; ii < 5; ii++) {
for (int jj = ii + 1; jj < 9; jj++) {
if (a[ii] > a[jj]) {
unsigned char temp = a[ii];
a[ii] = a[jj];
a[jj] = temp;
}
}
}
dst[i * width + j] = a[4];
}
}
for (int i = 0; i < width; i++) {
dst[i] = src[i];
dst[(height - 1) * width + i] = src[(height - 1) * width + i];
}
for (int i = 0; i < height; i++) {
dst[i * width] = src[i * width];
dst[i * width + width - 1] = src[i * width + width - 1];
}
}
Mat speed_MedianFilter(Mat src) {
int row = src.rows;
int col = src.cols;
unsigned char * data = (unsigned char *)src.data;
unsigned char *dst = new unsigned char[row * col];
MedianFilter(row, col, data, dst);
Mat res(row, col, CV_8UC1, dst);
return res;
}
int main() {
Mat src = cv::imread("F:\\t1.jpg", 0);
Mat dst1 = fastMedianBlur(src, 3);
Mat dst2 = speed_MedianFilter(src);
cv::imshow("dst1", dst1);
cv::imshow("dst2", dst2);
int row = src.rows;
int col = src.cols;
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
if (dst1.at<uchar>(i, j) != dst2.at<uchar>(i, j)) {
printf("%d %d\n", i, j);
}
}
}
system("pause");
cv::waitKey(0);
return 0;
}代码已经测试过,验证无误。在分辨率比较大的图像上执行中值滤波可以考虑一下这个算法,而且这个算法使用SSE指令可以进一步加速,后续会继续分享,欢迎大家关注阅读哦。
后记
今天为大家介绍了一个基于直方图的快速中值滤波算法,希望对大家有帮助。
欢迎关注我的微信公众号GiantPandaCV,期待和你一起交流机器学习,深度学习,图像算法,优化技术,比赛及日常生活等。

发布于 2019-12-18 23:01

